Брзина на светлината
| Дел од серијата |
| Специјална релативност |
|---|
 |
 На сончевата светлина ѝ требаат околу 8 минути и 19 секунди за да стигне до Земјата | |
| Точни вредности | |
|---|---|
| Метри во секунда | 299 792 458 |
| Планкови единици | 1 |
| Приближни вредности | |
| километри во секунда | 300 000 |
| километри на час | 1 080 милиони |
| астрономски единици дневно | 173[Забелешка 1] |
| Приближно време на патување на светлинскиот сигнал | |
| Растојание | Време |
| еден метар | 3,3 нс |
| од геостационарна орбита до Земјата | 119 мс |
| должина на Земјиниот екватор | 134 мс |
| од Месечината до Земјата | 1,3 с |
| од Сонцето до Земјата (1 ае) | 8,3 мин |
| од најблиската ѕвезда до Сонцето (1,3 пс) | 4,2 г. |
| од најблиската галаксија (Џуџеста галаксија во Големо Куче) до Земјата | 25 000 г. |
| низ Млечниот Пат | 100 000 г. |
| од галаксијата Андромеда до Земјата | 2,5 милиони г. |
| од Земјата до работ на видливата вселена | 46,5 милијарди г. |
Брзина на светлината, обично се бележи со латинично c[1] (лат. celeritas — брзина) — физичка константа важна во голем број области од физиката. Нејзината вредност (во вакуум) изнесува точно 299.792.458 м/сек. (≈3,00⋅108 м/с), односно 1.079.252.848,8 км/ч. Според Специјалната теорија на релативноста тоа е максималната брзина со која сета енергијата, материјата и сите информации можат да патуваат во универзумот, а која може да се постигне единствено во вакуум . Затоа често се обележува и со c0. Во други средини (течности, гасови...) брзината на светлината е различна и секогаш помала отколку во вакуум. Со брзината на светлината во вакуум се движат честичките кои немаат маса и електромагнетното зрачење (светлината и гравитациските бранови и се одвиваат промените во полињата. Тие ја задржуваат c без разлика на движењето на нивниот извор или на инерцијалниот појдовен систем на набљудувачот. Во Теоријата на релативноста c ги соединува просторот и времето и се појавува во познатата Ајнштајнова равенка за еднаквост на масата и енергијата E = mc2.[2]
Брзината со која светлината се пренесува низ проѕирни материјали (стакло, воздух...), а радиобрановите низ кабли, е помала од c. Односот меѓу c и v, брзината со која светлината патува низ одреден материјал, го дава показателот на прекршување n на материјалот (n = c / v). За видливата светлина показателот на прекршување на стаклото изнесува околу 1,5, што значи дека низ стаклото светлината патува со брзина од c / 1.5 ≈ 200.000 км/с. Показателот на прекршување на воздухот изнесува приближно 1.0003 за видливата светлина, што значи дека таа низ воздух се движи со брзина од 299.700 км/с (90 км/с побавно отколку со c). Со оглед дека светлината е облик на електромагнетно зрачење, нејзината брзина зависи од електричните и магнетните својства на средината низ која се движи и претставува константа за таа средина. Брзината на светлината се пресметува според формулата: , а во вакуум според формулата: [3].
Кога електромагнетните бранови треба да поминат големо растојание или при правење прецизни мерења, нивната конечна брзина значајно отстапува од c. За пристигање на пораки испратени од Земјата до далечни вселенски сонди, а и обратно, потребни се од неколку минути до неколку часа. Онаа светлина која ја емитуваат ѕвездите нив ги напуштила пред мноштво години, што значи дека ние ја гледаме и проучуваме историјата на вселената и вселенските објекти. Ограничената брзина на светлината ја ограничува и онаа која е теоретски максимум на сметачите, поради преносот на информациите од чип на чип. Затоа, пак, брзината на светлината овозможува мерење огромни растојанија со голема прецизност.
Првиот научник кој покажал дека светлината патува со определена, конечна брзина е Оле Ремер. Тоа го објавил во 1676 година по набљудувањето на движењето на Ија (една од месечините на Јупитер). Во 1865 година Џејмс Кларк Максвел претпоставил дека светлината е електромагнетен бран и затоа патува со брзината c спомената во неговата теорија на електромагнетизмот.[4] Во 1905 година Алберт Ајнштајн претпоставил дека брзината на светлината не зависи од движењето на светлинскиот извор во ниеден инерцијален појдовен систем,[5] а последиците од ваквата поставка ги истражил изведувајќи ја Специјалната теорија на релативноста и покажувајќи дека параметарот c не е важен само за светлината и електромагнетизмот.
По векови сè попрецизни мерења, во 1975 година брзината на светлината се сметала за 299 792 458 m/s, со грешки на 4 дела од милијарда. Во 1983 година SI го предефинирал метарот како растојание кое светлината го поминува во вакуум за 1/299 792 458 од секунда. Дефиницијата за метарот ја утврдила бројната вредност на брзината на светлината во вакуум c во метри во секунда.[6]
Бројна вредност, обележување и мерни единици[уреди | уреди извор]
Брзината на светлината во вакуум се бележи со малата латинична буква c (од латинското „celeritas“ што значи „брзина“. Максвел го користел и симболот V како алтернатива на c, во 1865 година. Во 1856 година Вилхелм Едуард Вебер и Рудолф Колрауш го употребувале c како константа со вредност √2 од брзината на светлината во вакуум. Денешната дефиниција за c ја дал Паул Друде 38 години подоцна, во 1894 година. И покрај тоа, Ајнштајн брзината на светлината ја означувал со V во своите оригинални трудови за Специјална релативност (на германски јазик) „Annus Mirabilis“ (латински, со значење „извонредна година“), но откако за стандарден симбол бил утврден c, тој во 1907 започнал да го користи него.[7][8]
Понекогаш c се употребува за означување на брзината на брановите во која било материјална средина, а c0 за брзината на светлината во вакуум.[9] Симболот со индекс 0 одобрен во официјална литература на SI[6] ја има истата форма како други константи - μ0 за пермеабилност на вакуум, вакуумската диелектрична константа ε0, Z0 за електрична импеданца на вакуум... Во оваа статија се употребува самоc како ознака и тоа само за брзина на светлината во вакуум.
Од 1983 година SI го дефинира метарот како растојанието кое го поминува светлината во вакуум за време од 1/299792458 секунди, поради што и брзината на светлината е фиксирана на точно 299 792 458 m/s.[10][11][12] Бројната вредност на брзината на светлината е различна во различни мерни системи, поради тоа што c е димензионална физичка константа. [Забелешка 2] Во физичките гранки (како релативноста) каде често се појавува c се користат и системи од природни единици мерки или геометризиран систем на мерки каде се зема c = 1.[14][15] Со овие мерни единици c не се јавува експлицитно (множење или делење со 1 не влијае на резултатот).
Фундаментална улога во физиката[уреди | уреди извор]
Брзината со која светлинските бранови се шират во вакуум е независна од движењето на светлинскиот извор и инерцијалниот појдовен систем на набљудувачот.[Забелешка 3] Ова независност на брзината на светлината е утврдена (постулирана) од страна на Ајнштајн во 1905 година,[5] кој бил поттикнат од Максвеловата теорија за електромагнетизмот и недостатокот од докази за постоењето на етерот.[16] Оттогаш бројните експерименти постојано го потврдуваат ова откритие. Експериментално може да се потврди дека само двонасочната брзина на светлината (на пример од светлински извор до огледало и назад) е зависна од појдовниот систем бидејќи е невозможно да се измери еднонасочната брзина (како од извор до далечен детектор) без постоење договорен начин за синхронизирање на часовникот кај изворот со оној при детекторот. Од друга страна, пак, преку Ајнштајнова синхронизација на часовниците, по дефиниција, доаѓа до изедначување на еднонасочната со двонасочната брзина на светлината.[17][18] Специјалната теорија на релативноста ги испитува последиците на таквата независност на c под претпоставка дека физичките закони важат подеднакво во сите инерцијални појдовни системи.[19][20] Една од последиците е што c мора да биде брзината со која сите безмасени честички и бранови се движат низ вакуум, вклучително и светлината.
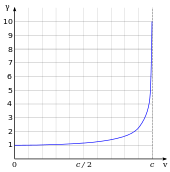
Специјалната релативност има многу контрадикторни и експериментално потврдени импликации.[21] Меѓу нив се вбројуваат еднаквоста на масата и енергијата (E = mc2), контракцијата на должината (предметите кои се во движење се скусуваат),[Забелешка 4] и дилатација на времето (часовниците во движење работат побавно). Факторот γ според кој должината се намалува, а времето забавува се нарекува Лоренцов фактор и се изразува како γ = (1 − v2/c2)−1/2, каде v е брзината на предметот. Разликата на γ од 1 е занемарлива при брзини многупати помали од онаа на светлината. Поради тоа што такви се мнозинството од секојдневните брзини, за нив наместо специјалната релативност може да се прифати дека, како приближно точна, важи Галилеевата релативност. До специјалната теорија на релативноста мора да се придржува при брзини поблиски до c зашто тогаш Лоренцовиот фактор се стреми кон бесконечност.
Резултатите од специјалната релативност се сумираат со третирањето на времето и просторот како обединета конструкција — време-простор ( c ги соединува времето и просторот) и со настојувањето физичките теории да ја задоволуваат специјалната симетрија — т.н. Лоренцова симетрија, чија математичка формула го содржи параметарот c.[24] Лоренцовата инваријантност е речиси универзална претпоставка на современите теории — Квантна електродинамика, Квантна хромодинамика, Стандардниот модел на честичната физика и Општата теорија за релативноста. Така, параметарот c е сеприсутен во современата физика бидејќи не се појавува секогаш само во врска со светлината. Општата релативност, на пример, предвидува дека c е воедно и брзина на гравитацијата и на гравитациските бранови.[25][26] Во неинерцијалните системи (простор закривен поради гравитацијата или забрзан појдовен систем) локалната брзина на светлината е постојана и еднаква на c, но долж траекторија со конечна должина таа може да се разликува од c во зависност од начинот на дефинирање на растојанијата и времето.[27]
Општо е земено дека основните константи, меѓу кои и c, ја задржуваат истата вредност низ време-просторот, односно таа ниту зависи од местоположбата ниту се менува со текот на времето. Сепак, во мноштво теории се појавува идејата дека брзината на светлината може да се променила со текот на годините.[28][29] Сѐ уште не постојат убедливи докази за такви промени, меѓутоа, преку натамошни истражувања, по нив и понатаму се трага.[30][31]
Уште една општа претпоставка е дека брзината на светлината е изотропна — нејзината вредност е еднаква без разлика на насоката на мерење. Можната двонасочна анизотропија има добиено строги гранични вредности како резултат на набљудувањата на емисија од јадрените енергетски нивоа, како функција од ориентираноста на јадрата во магнетното поле (експеримент на Хјуз и Древер) и на вртечки оптички резонатори.[32][33]
Горна граница на брзините[уреди | уреди извор]
Според Специјалната теорија за релативноста енергијата на предмет со маса на мирување m и брзина v изнесува γmc2, каде γ е Лоренцовиот фактор (дефиниран погоре). При v=0, γ=1, па оттука произлегува познатата формула за еднаквост на масата и енергијата: E = mc2. Факторот γ се стреми кон бесконечност како што v се приближува до c, значи за забрзување на објект со маса до брзината на светлината потребна е бесконечно голема енергија. Брзината на светлината е, всушност, горната граница за брзината која може да ја достигне кој било објект со позитивна маса на мирување. Поединечните фотони, пак, не можат да се движат со брзина поголема од онаа на светлината.[34][35] Тоа е експериментално утврдено во многу тестови на релативистичката енергија и импулс.[36]

Општо земено, во нормални услови е невозможно информациите и енергијата да патуваат со брзина поголема од c. Во прилог на ова тврдење е последицата од Специјалната релативност позната како Релативност на едновременоста. Ако просторното растојание меѓу два настана A и B е поголемо од временскиот интервал меѓу нив помножен со c, тогаш постојат и појдовни системи во A му претходи на B и системи каде B му претходи на A, па и такви појдовни системи во кои настаните се едновремени. Поради тоа, ако нешто патува со брзина поголема од c во однос на инерцијален појдовен систем, тоа ќе патува назад во времето во однос на друг појдовен систем, па причиноста ќе се наруши.[Забелешка 5][38] Во таков појдовен систем прво би се видела „последицата“, а дури подоцна „причината“. Досега не е регистрирано такво прекршување на причиноста,[18] кое би довело до парадокси како тахионскиот антителефон.[39]
Набљудување на натсветлински брзини и експерименти[уреди | уреди извор]
Постојат околности кога се чини дека материјата, енергијата или информациите патуваат побрзо од светлината, но не е така. Во делот подолу, за движењето на светлината во материјални средини, се вели дека многу бранови брзини можат да ја надминат c — фазната брзина на X-зраците низ стакло често минува со брзина поголема од c, на пример.[40] Сепак, фазната брзина не ја утврдува и брановата брзината на пренос на информации.[41]
Ако набрзина се помине со ласерски зрак преку далечен предмет, светлинската точка може да се има брзина поголема од c иако нејзиното почетно придвижување е задоцнето поради времето потребно за светлината да го помине растојанието. Единствените физички величини на ласерот кои се движат, пак, се ласерот и светлината која ја емитува (со брзина c) до различните местоположби на точката. Побрзо од светлината се движи и сенката проектирана врз далечен објект, по определено доцнење.[42] Во ниеден од двата случаи нема движење на материја, енергија или информации побрзо од светлината.[43]
Стапката на менување на оддалеченоста меѓу два предмета кои се движат во однос на даден појдовен систем (нивната брзина на приближување) може да биде поголема од c, но таа не претставува брзина на еден објект измерена во еден инерцијален систем.[43]
Одредени квантни ефекти изгледаат како да се предаваат моментално, што значи и побрзо од c, како во парадоксот на Ајнштајн—Подолски—Розен. Овој мисловен експеримент ги опфаќа квантните состојби на две честички кои можат да се вплеткаат. Сѐ додека се набљудува едната од нив, двете постојат во суперпозиција од две квантни состојби. Ако честичките се одвојат и се проследи квантната состојба само на едната од нив, во истиот миг се утврдува квантната состојба и на другата (за пократко време од она кое ѝ е потребно на светлината да стигне од едната до другата честичка). Затоа, пак, не може да се контролира која квантна состојба ќе ја заземе првата честичка кога ќе се набљудува, па не можат да се пренесат податоци.[43][44]
Друг квантен ефект кој предвидува појава на натсветлински брзини е Хартмановиот ефект — при извесни услови, времето потребно за виртуелна честичка да изведе тунелски ефект низ некоја пречка е постојано, без разлика на дебелината на препреката.[45][46] Тоа може да предизвика честичката да ја премине препреката со брзина поголема од онаа на светлината, но повторно без пренос на информации.[47]
Кај определени астрономски објекти се забележува т.н. суперлуминално движење (со брзина поголема од светлинската)[48] — такви се релативистичките млазови на радиогалаксиите и квазарите. Сепак, нивните брзини не ја надминуваат светлинската: привидното суперлуминално движење е само ефект на проекција предизвикан од телата кои со брзина на светлината се приближуваат кон Земјата под мал агол во однос на видната линија. Бидејќи на светлината емитирана кога млазот бил подалеку од Земјата ѝ било потребно подолго време да стигне до Земјата, времето меѓу две последователни набљудувања му одговара на подолг временски интервал меѓу моментите на емитирање на различните светлински зраци.[49]
Во моделите на вселена која се шири, колку галаксиите се подалеку една од друга, толку побрзо се оддалечуваат. Тоа не се должи на движењето низ просторот, туку на ширењето на вселената.[43] Така, галаксиите кои се далку од Земјата се чини дека уште повеќе се оддалечуваат од неа, со брзина пропорционална на нивната оддалеченост. По границата позната како Хаблова сфера стапката на зголемување на нивното растојание од Земјата е поголемо од брзината на светлината.[50]
Ширење на светлината[уреди | уреди извор]
Во класичната физика, светлината се опишува како вид електромагнетен бран. Класичното однесување на електромагнетно поле е опишано со Максвеловите равенки, според кои c со која електромагнетните бранови (како светлината) се шират во вакуум е поврзана со диелектричната константа ε0 и пермеабилноста на вакуумот μ0 и тоа преку релацијата c = 1/√ε0μ0.[51] Во современата квантна физика електромагнетното поле го опишува теоријата на квантна електродинамика, според која светлината е определена од квантите на електромагнетното поле - фотоните. Во оваа теорија фотоните се безмасени честички, поради што и можат да патуваат со c во вакуум, според специјалната теорија за релативноста.
Се разгледуваат и проширувања квантната електродинамика според кои фотонот има маса. Во таква теорија брзината би му зависела од честотата, а непроменливата c во специјалната релативност би била горната граница за брзината на светлината во вакуум.[27] При ригорозни тестирања не е забележано никакво варирање на брзината на светлината со честотата,[52][53][54] затоа масата на фотонот е строго ограничена. Граничната вредност зависи од моделот кој се користи: ако фотонот со маса се опише со теоријата на Прока,[55] неговата експериментална горна масена граница е околу 10−57 грама.[56], а според механизмот на Хигс границата не е толку строга, m ≤ 10−14 eV/c2 [55] (заокружено на 2 × 10−47 g).
Друга причина зошто брзината на светлината да варира со нејзината честота би било неважењето на специјалната теорија на релативноста за произволни мали размери, кое го предвидуваат предложените теории за квантна гравитација. Во 2009 година, проследувањето на спектарот на блесок од гама-зрачење не утврдило различни брзини кај фотоните со различни енергии. Тоа ја потврдило Лоренцовата инваријантност, барем до големината на Планковата должина (lP = √ħG/c3 ≈ 1,6163⋅10-35 м) поделена со 1,2.[57]
Во материјална средина[уреди | уреди извор]
Светлината не се движи со брзина еднаква на c во материјална средина. Различните видови светлина патуваат со различни брзини. Секој мев и јазол на рамнински бран (кој го исполнува целиот простор со само една честота) се движи со брзина наречена фазна брзина vф. Светлинскиот импулс (конечниот сигнал) патува со друга брзина. Најголемиот дел од импулсот се движи со групна брзина vг, а најраниот (почетниот) дел со челна брзина vч.
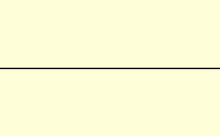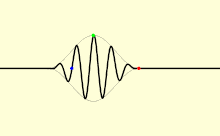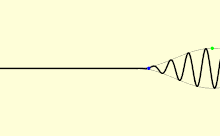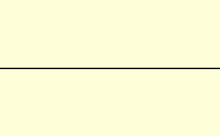
За определување на начинот на кој светлината минува низ некој материјал или од еден кон друг материјал важна е фазната брзина. Таа најчесто се претставува преку показателот на прекршување – односот на c и фазната брзина vф во средината. Следува дека поголем показател на прекршување значи помала брзина. Показателот на прекршување може да зависи и од честотата, интензитетот, поларизацијата или насоката на ширење на светлината. Сепак, почесто се смета за константа зависна само од средината. Показателот на прекршување на воздухот изнесува околу 1,0003.[58] Погустите материјални средини, како водата,[59] стаклото,[60] и дијамантот[61] имаат поголеми индекси на прекршување на видливата светлина (1,3, 1,5 и 2,4). Во материјалите како Бозе-Ајнштајновите кондензати, при апсолутна нула, делотворната брзина на светлината е само неколку метри во секунда. Меѓутоа ова е пример за апсорпцијата и доцнењето на преносот, како и сите други брзини помали од c во материјалните средини. Ектремна ситуација на „забавување“ на светлината во материја е постигната од два независни тима физичари кои тврделе дека „целосно ја запреле“ светлината емитувајќи ја низ Бозе-Ајнштајнов кондензат на рубидиум. Едната екипа го постигнала тоа на „Харвард“ и Институтот за наука „Роуланд“ во Кембриџ (Масачусетс), а другата во Центарот за астрофизика „Харвард-Смитсонијан“, исто така во Кембриџ. Ваквото „стопирање“ на светлината, всушност, се однесува на складирање на светлината во возбудените состојби на атомите, а потоа нејзино задоцнето ослободување поттикнато со втор ласерски импулс. Во периодот кога „застанала“, светлината престанала да биде светлина. Ваквиот однос е микроскопски точен за сите проѕирни материјални средини кои ја „забавуваат“ брзина на светлината.[62]
Во провидните материјали, показателот на прекршување е главно поголем од 1, па фазната брзина е помала од c. Во другите материјали, за определени честоти може да биде и помал од 1, па дури и негативен во необичните (егзотични) супстанции.[63] Барањето за ненарушеност на каузалноста подразбира дека реалните и комплексните делови на диелектричната константа на секој материјал, кои одговараат на соодветниот показател на прекршување и коефициент на апсорпција, се врзани преку Крамерс-Крониховите релации.[64] Тоа значи дека во средина чиј показател на прекршување е помал од 1, апсорпцијата на бранот е толку брза што ниеден сигнал не може да се испрати со брзина поголема од c.
Импулсот чија групна и фазна брзина се различни (што се случува кога фазната брзина не еднаква за сите честоти) со текот на времето дисперзира (се распрснува). Некои материјали имаат особено ниска (дури и нулта) групна брзина за светлинските бранови – феномен познат како бавна светлина, потврден со бројни експерименти.[65][66][67][68] И спротивното е експериментално покажано - групни брзини кои ја надминуваат c.[69] Треба да биде возможно дури и групната светлина да стане бесконечна или негативна така што импулсите ќе патуваат во моментално или, пак, назад во времето.[70]
Сепак, ниту една од овие можности не овозможува пренос на податоци побрзо од c. Невозможно е да предаваат информации преку светлински импулси со брзина поголема од челната, која, според некои претпоставки, е секогаш еднаква на c.[70]
Честица може да се движи низ материјална средина со брзина поголема од фазната брзина во таа средина, но сепак побавно од светлината во вакуум. Кога тоа се случува со наелектризирана честица во диелектрик, се емитира електромагнетниот еквивалент на ударен бран - Черенково зрачење.[71]
Практични ефекти на конечноста[уреди | уреди извор]
Брзината на светлината е значајна за телекомуникација: времето потребно за патување во една насока и назад е поголемо до нула. Ова важи од мали до астрономски сразмери. Но, токму конечноста на брзината на светлината е својството од кое зависат мерењата на оддалеченост, на пример.
Мали сразмери[уреди | уреди извор]
Брзината на светлината наметнува граница за брзината на праќање податоци, меѓу обработувачите на суперсметачите. Ако обработувачот работи при 1 GHz, за еден циклус сигналот може да помине растојание од најмногу 30 см. Затоа, за најоптимална работа обработувачите се поставуваат блиску едни до други, што, пак, предизвикува проблем за нивното ладење. Ако продолжи зголемувањето на часовничката честота, брзината на светлината веројатно ќе стане граничен фактор за внатрешниот дизајн на еден чип.[72]
Големи далечини на Земјата[уреди | уреди извор]
Со оглед на тоа дека полупречникот на Земјата изнесува околу 40 075 км, а c околу 300 000 км/с, теоретски најкусото време потребно за дел од информација да пропатува долж половина од Земјината топка е 67 милисекунди. Кога светлината патува околу Земјата низ оптичко влакно, пак, времето е подолго, делумно поради тоа што брзината на светлината е приближно 35% помала во влакното, зависно од неговиот показател на прекршување n.[73] Освен тоа, во глобалната комуникација сигналите ретко се движат по прави линии и без доцнење (поради минување на сигналот низа електричен прекинувач или сигнален регенератор).[74]
Вселенски летови и астрономија[уреди | уреди извор]

Комуникацијата меѓу Земјата и вселенските летала не е моментална. Постои кратко задоцнување од изворот до примачот кое станува сѐ поизразено со зголемување на оддалеченоста. Ова задоцнување било значајно и за размената на информации Центарот за управување со летови и Аполо 8 – првото вселенско летало кое ја обиколило Месечината, а било управувано од човек. Пристигањето на одговорот на секое прашање требало да се чека барем три секунди.[75] Доцнењето меѓу Земјата и Марс може да биде од пет до дваесет минути во зависност од релативната меѓусебна положба. Како последица, кога робот на површината на Марс би се соочил со некаков проблем, оние кои управуваат со него од Земјата нема да бидат свесни за тоа сѐ додека не поминат барем пет, а можеби и дваесет минути. Потоа би требало уште толку време за роботот да ја прими наредбата испратена од Земјата.
НАСА мора да чека неколку часа за да ги добие информациите од сонда која кружи околу Јупитер. Ако на истата ѝ е потребна навигациона исправка, постои ризик информациите за исправка на истата да пристигнат предоцна.
Примањето светлосни, а и други сигнали од далечните астрономски извори трае уште подолго. На светлината од галаксиите прикажани во сликата „Хаблово ултрадлабоко поле“ ѝ требале 13 милијарди (13×109) години за да пристигне до Земјата.[76][77] Фотографиите ги отсликуваат гралаксиите какви што биле пред 13 милијарди години, кога универзумот постоел помалку од милијарда години.[76] Тоа што подалечните предмети ни изгледаат помладо (поради ограничената брзина на светлината) им овозможува на астрономите да ја определат развојот на ѕвездите и галаксиите, како и на космосот воопшто.
Астрономските растојанија често се изразуваат во светлосни години, особено во публикациите и медиумите.[78] Светлосна година е растојанието кое светлината го поминува за една година - околу 9461 милијарди километри (заокружено на 10 трилиони км), односно 0,3066 пс. Најблиската ѕвезда до Земјата (освен Сонцето), Проксима Кентаур, е оддалечена од неа 4,2 светлосни години.[79]
Мерење растојание[уреди | уреди извор]
Утврдувањето на оддалеченоста на објектите се врши со радарски системи, преку испраќање и примање на одбиениот радиобран: растојанието е производ од половина од изминатото транзитно време и брзината на светлината. ГПС приемникот ја мери својата оддалеченост од ГПС сателитите според времето потребно за да добие радиосигнал од секој од нив, на тој начин определувајќи ја својата местоположба. Бидејќи светлината минува околу 300 000 км за една секунда, мерките во мали делови од секундата мораат да бидат сосема прецизни. Ласерската месечева локација, радиоастрономијата и Мрежата на длабоката вселена на НАСА служат за одредување на оддалеченоста на Месечината,[80] планетите[81] и вселенските летала,[82], мерејќи го двонасочното транзитно време.
Висопрометна трговија[уреди | уреди извор]
Брзината на светлината стана важна во високопрометната трговија, каде трговците тежнеат кон добивање мала предност преку испорака на стоката за дел од секунда порано од конкурентите. Така, тие употребуваат општење со микробранови поради нивната предност при преносот со брзина блиска до светлинската низ воздух, наместо оптички влакна низ кои сигналот се движи со брзина 30-40% помала од брзината на светлината низ стакло.[83]
Мерење на брзината на светлината[уреди | уреди извор]
Постојат бројни постапки за утврдување на вредноста на c. Еден од нив е мерење точно на брзина со која светлинските бранови се шират, преку астрономски поставки или поставки на Земјата. Меѓутоа, c може да се утврди и од физичките закони во кои се појавува, на пример од поврзаноста со електромагнетните константи ε0 и μ0. Најточните резултати биле добиени преку утврдување на честотата и брановата должина на еден светлински зрак, чијшто однос ја дава брзината на светлината c.
Во 1983 година метарот бил дефиниран како „делот од патот кој светлината го поминува за временски интервал од 1/299792458 секунда",[84] со што брзината на светлината била фиксирана на 299 792 458 m/s по дефиниција (како што е опишано подолу). Како последица на тоа, точните мерења на брзината на светлината повеќе придонесуваат за точна дефинираност на метарот отколку за точната вредност на c.
Астрономски мерења[уреди | уреди извор]

Со своето големо пространство и речиси совршен вакуум вселената е погодна средина за мерење на брзината на светлината. Се мери времето потребно за светлината да премине одредено референтно растојание во Сончевиот Систем (како полупречникот на Земјината орбита). Историски, ваквите мерења биле вршени доста точно во споредба со точноста со која се познавале растојанијата. Обично резултатите се изразуваат во астрономски единици на ден.
Оле Ремер ја направил првата квантитативна проценка на брзината на светлината со астрономско мерење.[85][86] Измерени од Земјата, периодите на орбитирање на сателитите на далечни планети се пократки кога Земјата се доближува кон нив во споредба со оние измерени кога таа се оддалечува. Растојанието кое светлината го минува од планетата (или нејзината месечина) е пократко кога Земјата е во точка на орбитата најблиска до планетата отколку кога Земјата е во најоддалечената точка. Разликата меѓу овие растојанија е пречникот на Земјината орбита околу Сонцето. Забележаната промена во периодот на сателитот е резултат на разликата меѓу времето потребно за светлината да го премости подолгото и покусото растојание. Овој ефект Ремер го забележал кај Ија, „највнатрешната“ месечина на Јупитер, па благодарение на него пресметал дека за поминување растојание еднакво на пречникот на Земјината орбита околу сонцето на светлината ѝ се потребни 22 минути.

Аберацијата на светлината може да послужи за друг метод на мерење на брзината на светлината, откриен и разјаснет од Џејмс Бредли во XVIII век.[87] Тоа е појава настаната поради собирање на векторите на брзината на светлината која доаѓа од далечен извор (како ѕвезда) и на брзината на набљудувачот (погледнете го дијаграмот десно). Така, набљудувач кој се движи гледа дека светлината доаѓа од малку поинаков правец, односно дека изворот се поместил од првобитната положба. Поради промената на Земјината брзина при кружењето околу Сонцето, аберацијата предизвикува положбата на ѕвездите да се поместува наоколу. Преку аголната разлика меѓу позицијата на ѕвездите (максмум 20,5 лачни секунди)[88] може да се изрази брзината на светлината во однос на Земјината брзина околу Сонцето која, познавајќи ја должината на годината, може да се претвори во времето потребно за патување од Сонцето до Земјата. Користејќи го овој метод, во 1729 година Бредли добил дека светлината патува 10 210 пати побрзо од Земјата во својата орбита (денес се зема 10 066 пати побрзо), односно за пристигање од Сонцето на Земјата на светлината и требаат 8 минути и 12 секунди.[87]
Астрономска единица[уреди | уреди извор]
Астрономска единица (ае) е приближното просечно растојание меѓу Земјатат и Сонцето. Во 2012 година е редефинирана како точно 149 597 870 700 m.[89][90] Таа претходно не се засновала врза Меѓународниот систем на мерни единици, туку врз гравитациската сила на Сонцето, во рамките на класичната механика. [Забелешка 6] Актуелната дефиниција ја користи препорачаната вредност во метри за претходната дефиниција на ае, утврдена со мерење.[89] Предефинирањето е аналогно на она на метарот, како и неговата цел – фиксирање на брзината на точно определна вредност во астрономски единици во секунда (преку точната брзина на светлината во метри во секунда).
Порадно, инверзната функција на c изразена во астрономски единици во секунда се мерела со споредба на времето потребно за радиосигналите да стигнат до разни вселенски летала во Сончевиот Систем. Нивната местоположба се пресметувала врз основа на гравитациските ефекти на Сонцето и планетите. Комбинирајќи ги различните измерени времиња се добивала најскладна вредност за брзината во единица должина. Најдобрата проценка одобрена од Меѓународниот астрономски сојуз во 2009 година била:[92][93]
- време на светлината за единица должина: 499,004783836(10) s;
- c = 0,00200398880410(4) ае/s = 173,144632674(3) ае/ден.
Релативната грешка при овие мерења е 0,02 дела на милијарда (2⋅10-11), што е еквивалентно на грешките при интерферометриските мерења извршени на Земјата.[94] Откако метарот е дефиниран како должина која светлината ја минува за одреден временски интервал, мерењето на светлинското време во однос на поранешната дефиниција за астрономската единица може да се толкува како мерење на должината на ае (според старата дефиниција) во метри.[Забелешка 7]
Техники на време на полетување[уреди | уреди извор]

Еден од методите за мерење на брзината на светлината е мерење на времето кое ѝ е потребно на светлината за да пристигне до огледало поставено на позната оддалеченост, да се одбие од него и да се врати назад. Врз овој принцип работи Физо-Фуковата апаратура (создадена од Ииполит Физо и Леон Фуко).
Конструкцијата која ја употребил Физо се состои од зрак светлина насочен кон огледало оддаелечено 8 километри. На патот од изворот до огледалото зракот минува низ вртечки запченик away. Со одредена стапка на вртење зракот минува низ една празнина патувајќи кон огледалото. Патувајќи низ друг отвор назад, со малку поголема или помала стапка зракот удира во забец и не поминува низ тркалото. Знаејќи го растојанието меѓу него и огледалото, бројот на запци и стапката на вртење може да се пресмета брзината на светлината.[95]
Фуковиот метод се разликува по тоа што наместо запченик се користи вртечко огледало. Поради неговата вртење при движењето на светлината до далечното огледало и назад, излегувајќи зракот се одбива под инаков агол од оној со кој се вратил. Во овој случај брзината на светлината може да се пресмета од разликата меѓу аглите, брзината на вртење и растојанието до далечното огледало.[96]
Денешните осцилоскопи кои го мерат времето со точност од околу една наносекунда овозможуваат директно мерење на брзината на светлината преку мерење на задоцнувањето на ласерски или ЛЕД светлински импулс рефлектиран од огледало. Оваа техника е помалку прецизна (со грешки во мерењето од редот на 1%) од другите современи техники, меѓутоа сѐ уште се користи при факултетски физчки лабораториски опити.[97][98][99]
Електромагнетни константи[уреди | уреди извор]
Една од можностите за утврдување на вредноста на брзината на светлината во вакуум, која не се темели врз нејзино директно мерење, е искористување на врската на c со диелектричната константа ε0 и пермеабилноста во вакуум μ0 утврдена од Максвел: c2 = 1/(ε0μ0). Диелектричната константа се одредува со мерење на електричниот капацитет и димензиите на кондензатор, а пермеабилноста е точно определена на 4⋅10-7 H.m-1 со дефиницијата на амперот. Со овој метод, Роза и Дорси за вредноста на c добиле 299 710 ± 22 км/с, во 1907 година.[100][101]
Шуплив резонатор[уреди | уреди извор]

Независното мерење на честотата f и брановата должина λ на електромагнетен бран во вакуум и нивната замена во релацијата c = fλ е уште еднен начин на одредување на брзината на светлината. Една од можностите е мерење на резонантната честота на шуплив резонатор. Со познати димензии на резонаторот може да се одреди брановата должина на бранот. Во 1946 година Луис Есен и Гордон-Смит ја утврдиле честотата на нормалните моди на микробрановите на микробранов резонатор, чии димензии биле познати, со точност од околу ±0.8 μm.[100] Брановата должина на модите била позната од геометријата на резонаторот и електромагнетната теорија, па познавањето и на честотите овозможило да се пресмета брзината на светлината.[100][102]
Резултатот (299 792 ± 9 км/с) кој го добиле Есен и Гордон-Смит бил значително попрецизен од резултатите добиени преку оптички техники.[100] Со постојано повторување на мерењата, до 1950 година Есен утврдил резултат од 299 792,5 ± 3,0 км/с.[103]
Оваа техника може да се испроба и во домашни услови, со помош на микробранова печка и маргарин или колачиња од бел слез. Ако се извади чинијата која се врти за храната да не се движи, тогаш таа најмногу ќе се испече и ќе почне да се топи кај мевовите на брановите (точките чија амплитуда е најголема). Растојанието меѓу две такви точки ја претставува брановата должина, која помножена со микробрановата честота (запишана на задната страна на микробрановата печка, обично околу 2450 MHz) ја дава вредноста на c can be calculated, „со грешка помала од 5%“.[104][105]
Интерферометрија[уреди | уреди извор]

Интерферометријата е уште еден метод за наоѓање на брановата должина на електромагнетно зрачење со цел определување на брзината на светлината.[106] Кохерентен зрак (како од ласер), чија честота (f) е позната, се дели и следи две патеки, кои потоа повторно се соединуваат. Со приспособување на должините на патеките при набљудување на интерферентната слика и внимателно мерење на нивната промена може да се одреди светлинската бранова должина (λ). Брзината на светлината се добива од релацијата c = λf.
Пред појавата на ласерската технологија, за интерферометриско мерење на брзината на светлината се користеле кохерентни радиоизвори.[107] Сепак, интерферометриското утврдување на бранова должина станува помалку прецизно со намалување на брановата должина. Поради тоа експериментите се ограничени со долгата бранова должина (~0.4 cm) на радиобрановите. Точноста се зголемува кај светлина чија бранова должина е помала, но затоа потешко е мерењето на нејзината честота. Еден начин да се надмине проблемот е започнување со нискофреквентен сигнал чија честота е мерлива, па од него постепено да се синтетизираат сигнали со повисоки честоти. Притоа високите честоти можат да се изразат преку мерливата. Преку интерферометрија може да се определи брановата должина доколку се фиксира ласер на постигнатата честота.[108] Ваквата техника ја осмислила група при Националниот институт за стандарди и технологија (тогашно Национално биро за стандарди и технологија), која во 1972 година ја измерила брзината на светлината во вакуум, со мерна несигурност од 3,5⋅10-9.[108][109]
Историјат[уреди | уреди извор]
| <1638 | Галилеј, покриени светилки | неопределена[Забелешка 8] |
| <1667 | Академија дел Чименто, покриени светилки | неопределена[Забелешка 9] |
| 1675 | Ремер и Хајгенс, сателити на Јупитер | 220 000[86][114] |
| 1729 | Џејмс Бредли, аберации на светлината | 301 000[95] |
| 1849 | Иполит Физо, назабено тркало | 315 000[95] |
| 1862 | Леон Фуко, вртечко огледало | 298 000 ± 500[95] |
| 1907 | Роза и Дорси, ЕМ константи | 299 710 ± 30[100][101] |
| 1926 | Алберт А. Мајкелсон, вртечко огледало | 299 796 ± 4[115] |
| 1950 | Есен и Гордон-Смит, шуплив резонатор | 299 792,5 ± 3,0[103] |
| 1958 | К.Д. Фрум, радиоинтерферометрија | 299 792,50 ± 0,10[107] |
| 1972 | Ивенсон и други, ласерска интерферометрија | 299 792,4562 ± 0,0011[109] |
| 1983 | Седумнаесетта ГКТМ, дефинирање на метарот | 299 792,458 (точна)[84] |
Дали светлината патува моментално или со многу голема конечна брзина не било познато сѐ до раниот нов век. Првите истражувања на оваа тема, кои постојат и денес, биле во Стара Грција. Хелените, исламските учени луѓе и класичните европски научници долго дебатирале во однос на ова прашање, сѐ до првата пресметка на брзината на светлината направена од Ремер. Ајнштајновата специјална теорија на релативноста заклучила дека таа брзина е постојана без оглед на појдовниот систем во кој се мери. Оттогаш спроведени се уште многу, попрецизни мерења.
Почетоци[уреди | уреди извор]
Емпидокле (околу 490–430 пр.н.е.) е првиот кој тврдел дека брзината има конечна брзина.[116] Тој наложувал дека светлината е нешто што се движи, та затоа потребно ѝ е време за да измине даден пат. Аристотел, пак, го тврдел спротивното – дека „светлината е резултат на присуство на нешто, но не претставува движење“.[117] Евклид и Птоломеј ја унапредлие Емпедоклевата емисиона теорија за видот, според која светлината потекнува од човечкото око и така го овозможува видот. Според оваа теорија Херон Александриски предложил дека брзината на светлината мора да е бесконечна затоа што далечните објектите, меѓу кои и ѕвездите, се појавуваат веднаш штом се отворат очите. Во индиските веди се споменуваат коментари на Сајана за мерењето на брзината на светлината. Раните исламски филозофи, пак, се сложувале со Аристотеловата физика (дека брзината нема брзина на движење. Алхазен ја издал „Книгата за оптиката“ во 1021 година, во која аргуметирано ја отфрлил емисионата теорија за видот, прифаќајќи ја интромисионата теорија дека светлината се движи од предметите кон очите.[118] Тој претпоставил и дека светлината мора да има конечна брзина[117][119][120] и дека е променлива – се намалува во погусти тела.[120][121] Според него светлината била реална материја за чие ширење е потребно време, дури и кога не е регистрирана од нашите сетила.[122] Во XI век Ел Бируни се согласил за конечноста на брзината на светлината и воедно заклучил дека е многу побрза од брзината на звукот.[123]
Роџер Бејкон, XIII век, тврдел дека брзината на светлината во воздух не е бесконечна, потпирајќи се на филозофските аргументи на Алхазен и Аристотел.[124][125] Во 1270-тите години, Витело ја зел предвид можноста за бесконечност на брзината на светлината во вакуум, а намаленост во погустите тела.[126]
Во раниот XVII век, Јоханес Кеплер верувал дека брзината на светлината е бесконечна поради отсуството на препреки во празниот простор. Рене Декарт, пак, сметал дека кога светлината би се движела со бесконечна брзина, тогаш Сонцето, Земјата и Месечината не би биле подредени во линија при затемнување на Месечината. Таква појава никогаш не била забележана, па Декарт бил уверен дека светлината не може да има бесконечна брзина. Ако некогаш се открие дека таа навистина е бесконечна, Декартовата филозофија ќе „падне во вода“.[117] Декарт во својата изведба на Снелиусовиот закон претпоставил дека иако брзината на светлината е мометална, колку е погуста материјалната средина низ која се шири толку брзината е поголема.[127] Пјер де Ферма го извел Снелиусовиот закон со спротивната претпоставка: колку е погуста средината толку е помала светлинската брзина. Ферма ја поддржувал конечноста на брзината на светлината.[128]
Први обиди за мерење[уреди | уреди извор]
Во 1692 година Исак Бекман предложил експеримент каде човек набљудува како блесок од топ се одбива од огледало оддалечено 1,6 км. Галилео Галилеј во 1638 година, пак, предложил опит (за кој тврдел дека го извел години претходно) за мерење на брзината на светлината набљудувајќи го доцнењето на светлината од ламба откриена на некоја оддалеченост од набљудувачот. Иако не можел да потврди дали светлината патува моментално, заклучил дека и ако не е така, таа сепак се движи извонредно брзо.[110][111] Академијата на експериментите во Фиренца пријавила дека го извела овој експеримент (во 1667 година) со растојание од една милја меѓу ламбите и притоа не било забележано никакво задоцнување. Задоцнувањето би требало да биде приближно 11 микросекунди.

Првата приближна пресметка на брзината на светлината била извршена во 1676 година од Ремер.[85][86] Набљудувајќи ги периодите на Ија, Јупитерова месечината најблиска до него, забележал дека тие биле пократки кога Земјата се доближувала до Јупитер отколку кога се оддалечувала. Заклучил дека светлината патувала со конечна брзина, проценувајќи дека ѝ се потребни 22 минути да го помине пречникот на Земјината орбита околу Сонцето. Кристијан Хајгенс ја комбинирал оваа проценка со таа за пречникот на Земјината орбита и добил вредност за брзината на светлината 26% помала од вистинската - 220 000 км/с.[114]
Исак Њутн ги изнел Ремеровите пресметки на конечната брзина на светлината во неговата книга „Оптикс“ (1704). Тој навел и дека светлината пристигнува од Сонцето до Земјата за „седум или осум минути“ (современо прифатената вредност е 8 минути и 19 секунди).[129] Њутн се запрашал дали Ремеровите сенки на затемнување биле обоени, а слушајќи дека не биле, сфатил дека различните бои патуваат со иста брзина. Џејмс Бредли, пак, ја открил аберацијата на светлината во 1729 година,[87] утврдувајќи од ефектот дека светлината мора да патува 10 210 пати побрзо отколку што Земјата се движи оболу Сонцето (современо: 10 066 пати побрзо), односно дека за да стигне од Сонцето до Земјата потребни ѝ се 8 минути и 12 секунди.[87]
Врска со електромагнетизмот[уреди | уреди извор]
Во XIX век Иполит Физо создал посебен метод за утврдување на брзината на светлината, добивајќи ја вредноста од 315 000 км/с. Методот го усовршил Леон Фуко, кој добил врдност од 298 000 км/с (1862 година).[95] Во 1856 година Вилхелм Едуард Вебер и Рудолф Колрауш го измериле односот меѓу електромагнетната и електростатичката единица полнеж, 1/√ε0μ0, ослободувајќи ја Лајденовата тегла од полнежот, па сфатиле дека неговата бројна вредност е многу блиска до онаа измерена за брзината на светлината од Физо.Густав Роберт Кирхоф пресметал дека електричниот сигнал патува со истата таа брзина низ жица без електричен отпор.[130] Во раните 1860-ти, Максвел покажал дека, според теоријата за електромагнетизам на која работел, електромагнетните бранови се шират низ празен простор[131][132][133] со брзина еднаква на Вебер-Колраушовиот размер. Тој ја предложил идејата за електромагнетната природа на светлината, потпирајќи се на блискоста на нејзината брзина со брзината измерена од Физо.[134]
Проблемот со етерот[уреди | уреди извор]

На почетокот на XX век се сметало дека празниот простор е исполнет со хипотетична еластична материја, т.н. етер во кој постои електромагнетно поле. Некои физичари етерот го сметале за привилегиран инерцијален систем низ кој се шират светлинските бранови, па затоа треба да може да се измери движењето на Земјата во однос на него и тоа преку мерење на изотропијата на брзината на светлината. Во 1880-тите започнале експерименти со цел да се регистрира ова движење, а меѓу нив најпознат е опитот на Алберт Мајкелсон и Едвард Морли од 1887 година.[135] Детектираното движење секогаш било помало од грешката при набљудувањето. Современите експерименти укажуваат дека двонасочната брзина на светлината е изотропна (иста во сите насоки) до 6 нанометри во секунда.[136] Овој експеримент го поттикнал Хендрик Лоренц да ја воведе идејата дека движењето на апаратурата низ етерот можеби предизвикува нејзина контракција (скусување) долж насоката на движење. Тој претпоставил и дека и времето мора да се менува, па тоа го навело да ги напише т.н. Лоренцови трансформации. Според неговата теорија за етерот, Анри Поанкаре (1900) покажал дека „месното време“ го покажуваат часовници кои се движат низ етерот, синхронизирани под претпоставката за постојана брзина на светлината. Во 1904 година шпекулирал дека е можно брзината на светлината да е гранична брзина во динамиката, секако ако сите Лоренцови претпоставки се потврделе. Во 1905 година Поенкаре целосно ја усогласил Лоренцовата теорија за етерот со принципот на релативноста.[137][138]
Специјална релативност[уреди | уреди извор]
Во 1905 година Ајнштајн постулирал дека брзината на светлината во вакуум, измерена од страна на набљудувач кој нема забрзување, не зависи од движењето изворот и набљудувачот. Овој принцип и принципот за релативноста му послужиле како основа за специјалната теорија на релативноста, каде c се смета за фундаментална константа. Ова било причината за отфрлање на теоријата за постоење неподвижен етер, но истовремено и за револуционизирање на концептите за просторот и времето.[139][140]
Зголемена точност на вредноста на c и предефинирање на метарот и секундата[уреди | уреди извор]
Најголем напредок во веродостојноста на измерените вредности за c е постигнат во втората половина на XX век, како резултат на шупливите резонатори, а потоа ласерските интерферометриски техники. Ним во прилог им оделе и новите, попрецизни дефиниции за метарот и секундата. Во 1950 година Луис Есен со помош на шуплив резонатор ја определил брзина на светлината како 299 792,5 ± 1 км/с. Вредноста била официјално прифатена на Дванаесеттото генерално собрание на Радионаучниот сојуз во 1957 година. Три години подоцна е редефиниран метарот, во однос на брановата должина на специфична спектрална линија на криптон-86. Секундата била предефинирана во 1967 година и тоа во однос на хиперфината транзициона честота на природната форма на цезиумот, цезиум-133.
Преку ласерски интерферометриски метод, група од Националниот институт за стандарди и технологија во Колорадо во 1972 година ја определила брзината на светлината во вакуум како c = 299 792 456,2 ± 1,1 m/s (со 100 пати помала несигурност од претходно прифатената вредност). Останатата мерна несигурност била поврзана со дефиницијата за метарот.[Забелешка 10][109] Сличнита експерименти резултирале со споредливи вредноси за c, па Петнаесеттата генерална конференција за тегови и мери во 1975 година препорачала употреба на 299 792 458 m/s како вредност за брзината на светлината.[143]
Дефинирање на брзината на светлината како посебна константа[уреди | уреди извор]
Седумнаесеттата ГКТМ во 1983 година увидела дека брановите должини од честотните мерења и прифатената вредност за брзината на светлината полесно се репродуцираат од претходните стандарди. Ја задржила дефиницијата за секундата од 1967 година, па цезиумовата хиперфина честота станала таа која ги одредува и секундата и метарот. За таа цел метарот бил предефиниран: „метар е должината на патот изминат од светлината во вакуум за времески интервал од 1/299792458 дел од секунда.“[84] Поради ваквата дефиниција, брзината на светлината во вакуум е точно 299 792 458 m/s[144][145] и затоа станата е дефинирана константа во SI.[12] Унапредените експериментални техники со кои би се мерела брзината на светлината пред 1983 година веќе не влијаат на познатата вредност за брзината на светлината. Тие само овозможуваат попрецизно дефинирање на метарот со поточно мерење на брановата должина на криптон-86 и другите светлински извори.[146][147]
Во 2011 година ГКТМ ја изрази намерата за редефинирање на сите седум основни мерни единици во SI преку т.н. „формулација на „експлицитна константа““, каде секоја „мерна единица е дефинирана индиректно преку посебно прецизирање на точната вредност за добропозната фундаментална константа“, како што е направено со брзината на светлината. Таа овозможи нова, а сосема еквивалентна формулација на дефиницијата: „метарот, симбол m, е единица за должина; нејзината големина е одредена со фиксирање на бројната вредност за брзината на светлината на точно 299 792 458 кога е изразена во SI-единицата m s−1."[148] Оваа е една од предложените промени планирани за следната ревизија на SI (новиот SI).
Поврзано[уреди | уреди извор]
Белешки[уреди | уреди извор]
- ↑ Точна вредност:
(299 792 458 × 60 × 60 × 24 / 149 597 870 700) ае/ден - ↑ Брзината на светлината во империјалниот мерен систем (на ВБ) и мерниот систем на САД е заснована на инчи (2,54 см), па изнесува 186 282 милји, 698 јарди, 2 стапки и 5 21127 инчи со секунда.[13]
- ↑ Сепак, светлинската честота може да зависи од придвижувањето на изворот во однос на набљудувачот поради Доплеровиот ефект.
- ↑ Освен што е измерено дека објектите во движење се пократки по во правецот на релативно движење, тие се гледаат и како вртечки тела. Ефектот, Терелово вртење, се должи на различното време кое ѝ е потребно на светлината за да пристигне до набљудувачот од различните делови на објектот.[22][23]
- ↑ Се смета дека Шарнхостовиот ефект им овозможува на сигналите да се движат малку побрзо од светлината во вакуум, меѓутоа посебните услови кои ја овозможуваат ваквата појава спречуваат употреба на ефектот за нарушување на причиноста.[37]
- ↑ Астрономската единица се дефинирала како полупречникот на непопречената Њутнова орбита околу Сонцето на честица со бесконечно мала маса, која се движи со аголна честота од 0,01720209895 радијани (приближно 1/365,256898 од Сончевиот развој) на ден.[91]
- ↑ Сепак, при толкава прецизност, при читање на должината мора да се земат предвид ефектите на општата релативност. Метарот се смета за мерна единица за должината на телото во појдовен систем кој мирува, а астрономската единица се користи како единица за бележење на набљудуваната должина во даден појдовен систем. Овдешните вредности ја следат втората претворба и се компатибилни со барицентричното динамично време.[93]
- ↑ Галилеј (1954),[110] Бојер (1941),[111] Фоши и Леоне (2009, стр. 1252).[112] Според Галилеј, светилките кои ги користел биле „на многу мало растојание, помалку од една милја“. Под претпоставка дека растојанието не било многу пократко од една милја и дека „најкраткиот временски интервал кој може да го издвои човечкото око е триесетти дел секунда“, Бојер забележал дека Галилеевиот експеримент, во најдобар случај ја утврдил долната граница на брзината на светлината на околу 96,5 километри во секунда.
- ↑ Магалоти (1667, стр.265–6),[113] Фоши и Леоне (2009, стр. 1253).[112]
- ↑ Меѓу 1960 и 1983 година метарот се дефинирал како: „метарот е должината еднаква на 1 650 763,73 бранови должини во вакуум на зрачењето кое одговара на преминот меѓу нивоата 2p10 и 5d5 во атомот криптон-86.“[141] Во 1970-тите се открило дека спектралната линија не е симетрична, па се ограничила реализацијата на дефиницијата во интерферометриските експерименти.[142]
Наводи[уреди | уреди извор]
- ↑ Гибс, П. (2004) [1997]. „„Зошто c е ознака за брзината на светлината?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Архивирано од изворникот 2009-11-17. Посетено на 20 април 2011.
- ↑ Узан, Ж.-Ф.; Леклерк, B (2008). „Природните закони на универзумот: Разбирање на фундаменталните константи“. „Springer“. стр. 43–4. ISBN 0-387-73454-6.
- ↑ Херис, Џ.В.; и др. (2002). „Прирачник за физика“. „Springer“. стр. 499. ISBN 0-387-95269-1.
- ↑ „„Како е измерена брзината на светлината?"“.
- ↑ 5,0 5,1 Стачел, Џ.Џ. (2002). „Ајнштајн од „B“ до „Z““ – Том 9 од Ајнштајовите студии. „Springer“. стр. 226. ISBN 0-8176-4143-2.
- ↑ 6,0 6,1 Меѓународно биро за тегови и мерки (2006), Меѓународен систем на мерни единици (SI) (PDF) (VIII. изд.), стр. 112, ISBN 92-822-2213-6 (англиски)
- ↑ Гибс, П. (2004) [1997]. „„Зошто c е ознака за брзината на светлината?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Архивирано од изворникот 2009-11-17. Посетено на 16 ноември 2009. „Употребата на буквата „c“ како ознака за брзината на светлината водат потекло еден труд на Вебер и Колрауш од 1856 година [...] Вебер имал намера c да означува „константа“ во неговиот закон за силата, но има докази дека физичарите како Лоренц и Ајнштајн се навикнале на конвенцијата c да се користи како променлива за брзина. Ваквата употреба има корени дури и во класични текстови на латински јазик каде c стои наместо '„celeritas“' што значи 'брзина'.“
- ↑ Менделсон, К.С. (2006). „„Приказната за „c""“. „American Journal of Physics“. 74 (11): 995–997. Bibcode:2006AmJPh..74..995M. doi:10.1119/1.2238887.
- ↑ Пример:
- Лиде, Д.Р. (2004). „CRC прирачник по хемија и физика“. „CRC Press“. стр. 2–9. ISBN 0-8493-0485-7.
- Херис, Џ.В.; и др. (2002). „Прирачник по физика“. „Springer“. стр. 499. ISBN 0-387-95269-1.
- Витакер, Џ.С. (2005). „Прирачник по електроника“. „CRC Press“. стр. 235. ISBN 0-8493-1889-0.
- Коен, Е.Р.; и др. (2007). „Бројни вредности, единици мерки и симболи во физичката хемија“ (трето издание. изд.). Кралско друштво на хемичари. стр. 184. ISBN 0-85404-433-7.
- ↑
Сиденхам, П.Х. (2003). „„Мерење должина"“. Во Бојс, В. (уред.). „Книга со наводи за инструментација“ (трето издание. изд.). „Батервуд-Хајнеман“. стр. 56. ISBN 0-7506-7123-8.
„... ако брзината на светлината е дефинирана како фиксиран број, тогаш, во принцип, стандардите за време ќе служат и како стандарди за должина ...“
- ↑ „„Вредност од „Комитетот за податоци за науката и технологијата": Брзината на светлината во вакуум"“. „Наводи на НИСТ за константи, мерни единици и неопределност“. НИСТ. Посетено на 21 август 2009.
- ↑ 12,0 12,1 Џесперсен, Џ.; Фиц-Рендолф, Џ.; Роб, Џ. (1999). „Од сончеви до атомски часовници: Разбирање на времето и честотата“ (второ издание, реиздание од „Националното биро за стандарди“ 1977 г.. изд.). „Courier Dover“. стр. 280. ISBN 0-486-40913-9.
- ↑ Сејвард, Џ. „„Од златни монети до кадмиумови светилки"“. Архивирано од изворникот 2009-11-14. Посетено на 14 ноември 2009.
- ↑ Лаури, И.Д. (2002). „„Додаток Ц: Природни единици мерки"“. „Обединета обиколка на теоретската физика“ (второ издание. изд.). „CRC Press“. стр. 540. ISBN 0-7503-0604-1.
- ↑ Хсу, Л. (2006). „„Додаток А: Системи мерни единици и развојот на релативистичките теории"“. „Поширок поглед на релативноста: Општи последици на непроменливоста на Лоренц и Поенкаре“ (второ издание. изд.). „World Scientific“. стр. 427–8. ISBN 981-256-651-1.
- ↑ Ајнштајн, А. (1905). „„Zur Elektrodynamik bewegter Körper" („За електродинамиката на подвижните тела")“. „Annalen der Physik“ (германски). 17: 890–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. Англиски превод: Перет, В.; Џефери, Г.Б. (прев.); Вокер, Џ.(уред.). „„On the Electrodynamics of Moving Bodies"“. Fourmilab. Посетено на 27 ноември 2009.
- ↑ Хсу, Ж.-П.; Жанг, Ј.З. (2001). „Лоренцова и Поенкареова инваријантност“. „Advanced Series on Theoretical Physical Science“. 8. „World Scientific“. стр. 543ff. ISBN 981-02-4721-4.
- ↑ 18,0 18,1 Жанг, Ј.З. (1997). „Специјалната релативност и нејзините експериментални основи“. „Advanced Series on Theoretical Physical Science“. 4. „World Scientific“. стр. 172–3. ISBN 981-02-2749-3. Архивирано од изворникот на 2012-05-19. Посетено на 2015-10-15.
- ↑ д’Инверно, Р. (1992). „Запознавање со Ајнштајновата релативност“. „Oxford University Press“. стр. 19–20. ISBN 0-19-859686-3.
- ↑ Сриранџан, Б. (2004). „„Постулатите на теоријата за специјална релативност и нивните последици"“. „Специјална теорија за релативноста“. „PHI Learning Pvt. Ltd.“. стр. 20 ff. ISBN 81-203-1963-X.
- ↑ Робертс, Т.; Шлајф, С.; Длукож, Џ.М.; и др. (2007). „„Кои се експерименталните основи на специјалната релативност?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Посетено на 27 ноември 2009.
- ↑ Терел, Џ. (1959). „„Невидливоста на Лоренцовата контракција"“. „Physical Review“. 116 (4): 1041–5. Bibcode:1959PhRv..116.1041T. doi:10.1103/PhysRev.116.1041.
- ↑ Пенроуз, Р. (1959). „„Очигледниот облик на сфера во релативно движење"“. „Proceedings of the Cambridge Philosophical Society“. 55 (01): 137–9. Bibcode:1959PCPS...55..137P. doi:10.1017/S0305004100033776.
- ↑ Хартл, Џ.Б. (2003). „Гравитација: Вовед во Ајнштајновата општа релативност“. „Addison-Wesley“. стр. 52–9. ISBN 981-02-2749-3.
- ↑ Хартл, Џ.Б. (2003). „Гравитација: Вовед во Ајнштајновата општа релативност“. Addison-Wesley. стр. 332. ISBN 981-02-2749-3.
- ↑ Некои автори не ја сметаат за веродостојна интерпретацијата на набљудувањата на двојни системи користени за утврдување на брзината на гравитацијата, поради што експериментите во таа насока се несигурни. Видете Шефер, Г.; Бригман, М.Х. (2008). „„Ширење на светлината низ гравитациското поле на двојните системи до квадратен ред на Њутновата гравитациска константа: Трета глава: „За контроверзијата на брзината на гравитацијата""“. Во Дитус, Х.; Лемерцел, Ц.; Туришев, С.Г. (уред.). „Ласери, часовници и контрола без влечење: Испитување на релативната гравитација во вселената“. „Springer“. ISBN 3-540-34376-8.
- ↑ 27,0 27,1 Гибс, П. (1997) [1996]. Карлип, С. (уред.). „„Дали брзината на светлината е постојана?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Архивирано од изворникот 2009-11-17. Посетено на 26 ноември 2009.
- ↑
Елис, Г.Ф.Р.; Узан, Ж.-Ф. (2005). „„'c' е брзина на светлината, зарем не?"“. „American Journal of Physics“. 73 (3): 240–7. arXiv:gr-qc/0305099. Bibcode:2005AmJPh..73..240E. doi:10.1119/1.1819929.
Можноста за варирање на фундаменталните константи во текот на развојот на универзумот отвора можност за продлабочување на теориите за повеќедимензионалност и веројатно е поврзана со природата на темната енергија – двигател на денешното забрзување на вселената.
- ↑ Преглед се содржи во дисертацијата на Мота, Д.Ф. (2006). "„Варијации на константата на фината структура во времето и просторот“". arXiv:astro-ph/0401631 [astro-ph].
- ↑ Узан, Ж.-Ф. (2003). „„Фундаменталните константи и нивната променливост: набљудувачки статус и теоретски мотивации"“. „Reviews of Modern Physics“. 75 (2): 403. Bibcode:2003RvMP...75..403U. doi:10.1103/RevModPhys.75.403.
- ↑ Амелино-Камелија, Г (2013). „Квантно-гравитациска феноменологија“. Living Reviews in Relativity. 16 (1): 5. arXiv:0806.0339. Bibcode:2013LRR....16....5A. doi:10.12942/lrr-2013-5. PMC 5255913. PMID 28179844.
- ↑ Херман, З.; и др. (2009). „„Тестирање на Лоренцовата инваријантност на 10−17 ниво преку експеримент со вртечки оптички резонатор"“. „Physical Review D“. 80 (100): 105011. arXiv:1002.1284. Bibcode:2009PhRvD..80j5011H. doi:10.1103/PhysRevD.80.105011.
- ↑ Ланг, К.Р. (1999). „Астрофизички формули“ (трето издание. изд.). „Birkhäuser“. стр. 152. ISBN 3-540-29692-1.
- ↑ „Официјално е: временските машини нема да функционираат“, „Los Angeles Times“, 25 јули 2011 година
- ↑ „Професори од УНТХК докажаа дека поединечните фотони не ја надминуваат брзината на светлината
- ↑ Фаулер, М. (март 2008). „„Белешки за специјалната релативност"“ (PDF). Универзитет на Виџинија. стр. 56. Посетено на 7 мај 2010.
- ↑ Либерати, С.; Сонего, С.; Висер, М. (2002). „„Сигнали побрзи од c, специјална релативност и причиност"“. Annals of Physics. 298 (1): 167–85. arXiv:gr-qc/0107091. Bibcode:2002AnPhy.298..167L. doi:10.1006/aphy.2002.6233.
- ↑ Тејлор, Е.Ф.; Вилер, Џ.А. (1992). „Физика на време-просторот“. В.Х. Фримен. стр. 74–5. ISBN 0-7167-2327-1.
- ↑ Толман, Р.С. (2009) [1917]. „„Брзини поголеми од светлинската"“. „Теорија на релативноста на движењето“ (преиздадена. изд.). „BiblioLife“. стр. 54. ISBN 978-1-103-17233-7.
- ↑ Хехт, Е. (1987). „Оптика“ (второ издание. изд.). „Addison-Wesley“. стр. 62. ISBN 0-201-11609-X.
- ↑ Квимби, Р.С. (2006). „Фотоника и ласери: вовед“. „John Wiley and Sons“. стр. 9. ISBN 978-0-471-71974-8.
- ↑ Вертхајм, М. (20 јуни 2007). „„Сенката заминува"“. „The New York Times“. Посетено на 21 август 2009.
- ↑ 43,0 43,1 43,2 43,3 Гибс, П. (1997). „„Дали се остварливи патување или комуникација побрзи од светлината?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Архивирано од изворникот 2009-11-17. Посетено на 20 август 2008.
- ↑ Сакураи, Џ.Џ. (1994). Т., С. (уред.). „Современа квантна механика“ (Revised. изд.). „Addison-Wesley“. стр. 231–232. ISBN 0-201-53929-2.
- ↑ Муга, Ј..Г.; Мајато, Р.С.; Егусквиза, И.Л. (2007). „Времето во квантната механика“. „Springer“. стр. 48. ISBN 3-540-73472-4.
- ↑ Hernández-Figueroa, Х.Е.; Zamboni-Rached, М.; Recami, Е. (2007). „Локализирани бранови“. „Wiley Interscience“. стр. 26. ISBN 0-470-10885-1.
- ↑ Вин, К. (2002). „„Жртвата и природата на информациите"“ (PDF). „Optics Communications“. 209 (1–3): 84–100. Bibcode:2002OptCo.209...85W. doi:10.1016/S0030-4018(02)01638-3.[мртва врска] архива
- ↑ Рис, М. (1966). „„Појавата на радиоизвори кои релативистички се шират"“. „Nature“. 211 (5048): 468. Bibcode:1966Natur.211..468R. doi:10.1038/211468a0.
- ↑ Чејс, И.П. „„Привидната надсветлинска брзина на галаксиите"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Посетено на 26 ноември 2009.
- ↑ Харисон, Е.Р. (2003). „Маските на универзумот“. „Cambridge University Press“. стр. 206. ISBN 0-521-77351-2.
- ↑ Панофски, В.К.Х.; Филипс, М. (1962). „Класичен електрицитет и магнетизам“. „Addison-Wesley“. стр. 182. ISBN 978-0-201-05702-7.
- ↑ Шефер, Б.Е. (1999). „„Строги граници на варијациите на брзината на светлината со честотата"“. „Physical Review Letters“. 82 (25): 4964–6. arXiv:astro-ph/9810479. Bibcode:1999PhRvL..82.4964S. doi:10.1103/PhysRevLett.82.4964.
- ↑ Елис, Џ.; Мавроматос, Н.Е.; Нанопулос, Д.В.; Сакхаров, А.С. (2003). „„Квантно-гравитациска анализа на изливи од гама-зраци со брановидни осцилации"“. „Astronomy & Astrophysics“. 402 (2): 409–24. arXiv:astro-ph/0210124. Bibcode:2003A&A...402..409E. doi:10.1051/0004-6361:20030263.
- ↑ Филеркруг, М. (2004). „„Испитување на брзината на светлината со радиобранови при екстремно ниски честоти"“. „Physical Review Letters“. 93 (4): 043901. Bibcode:2004PhRvL..93d3901F. doi:10.1103/PhysRevLett.93.043901.
- ↑ 55,0 55,1 Аделбергер, Е.; Двали, Г.; Грузинов, А. (2007). „„Photon Mass Bound Destroyed by Vortices"“. „Physical Review Letters“. 98 (1): 010402. arXiv:hep-ph/0306245. Bibcode:2007PhRvL..98a0402A. doi:10.1103/PhysRevLett.98.010402. PMID 17358459.
- ↑ Сидхарт, Б.Г. (2008). „Термодинамичкиот универзум“. „World Scientific“. стр. 134. ISBN 981-281-234-2.
- ↑ Амелино-Камелија, Г. (2009). „„Астрофизика: Излив на поддршка за релативноста"“. „Nature“. 462 (7271): 291–292. Bibcode:2009Natur.462..291A. doi:10.1038/462291a. PMID 19924200.
- ↑ де Подеста, М. (2002). „Разбирање на својствата на материјата“. „CRC Press“. стр. 131. ISBN 0-415-25788-3.
- ↑ „„Показател на прекршување на водата, H20 [Течности]"“. refractiveindex.info. Микаил Полијански. Посетено на 14 март 2010.
- ↑ „„Показател на прекршување на Кварцово стакло [Стакла]"“. refractiveindex.info. Микаил Полијански. Посетено на 14 март 2010.
- ↑ „„Показател на прекршување на C [Кристали итн.]"“. refractiveindex.info. Микаил Полијански. Посетено на 14 март 2010.
- ↑ „Harvard News Office“ (24 јануари 2001). „„Харвард гласник: Истражувачите сега можат да ја сопрат, реемитуваат светлината"“. News.harvard.edu. Посетено на 8 ноември 2011.
- ↑ Милони, П.В. (2004). „Брза светлина, бавна светлина и леворака светлина“. „CRC Press“. стр. 25. ISBN 0-7503-0926-1.
- ↑ Тол, Џ.С. (1956). „„Казуалноста и релацијата на дисперзија: логички темели"“. „Physical Review“. 104 (6): 1760–1770. Bibcode:1956PhRv..104.1760T. doi:10.1103/PhysRev.104.1760.
- ↑ Хау, Л.В.; Харис, С.Е.; Датон, З.; Берози, Ц.Х. (1999). „„Намалување на брзината на светлината на 17 метри во секунда во ултрастуден амоски гас"“ (PDF). „Nature“. 397 (6720): 594–598. Bibcode:1999Natur.397..594V. doi:10.1038/17561.
- ↑ Лиу, Ц.; Датон, З.; Берози, Ц.Х.; Хау, Л.В. (2001). „„Набљудување на кохерентно складирање информации во атомски медиум со употреба на светлински импулси"“ (PDF). „Nature“. 409 (6819): 490–493. Bibcode:2001Natur.409..490L. doi:10.1038/35054017. PMID 11206540.
- ↑ Бајси, М.; Зибров, А.С.; Лукин, М.Д. (2003). „„Неподвижни светлински импулси во атомски медиум"“. „Nature“. 426 (6967): 638–41. arXiv:quant-ph/0311092. Bibcode:2003Natur.426..638B. doi:10.1038/nature02176. PMID 14668857.
- ↑ Думе, Б. (2003). „„Пелење и гасење на светлината"“. „Physics World“. Институт за физика. Архивирано од изворникот на 2008-12-05. Посетено на 8 декември 2008.
- ↑ Вајтхаус, Д. (19 јули 2000). „„Зрак ја собори светлинската граница"“. „BBC News“. Посетено на 8 декември 2008.
- ↑ 70,0 70,1 П.В. Милони (2004). „2“. „Брза светлина, бавна светлина и леворака светлина“. „CRC Press“. ISBN 0-7503-0926-1.
- ↑ Черенков, Павел А. (1934). „„Видимое свечение чистых жидкостей под действием γ-радиации"“. „Doklady Akademii Nauk SSSR“. 2: 451. Преиздадено во „Usp. Fiz. Nauk“ 93 (1967) 385 и во „Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie“ А.Н. Горбунов и Е.П. Черенкова, Москва, „Nauka“ (1999) стр. 149–153.
- ↑ Пархами, Б. (1999). „Запознавање со паралелна обработка: алгоритми и архитектури“. „Plenum Press“. стр. 5. ISBN 978-0-306-45970-2. и Ајмбс, Д.; Рејнал, Мајкл (2009). В. Малишкин (уред.). „Софтверски трансакциони мемории: Пристап за повеќејадрено програмирање“. Десетта интернационална конференција „PaCT 2009“, Новосибирск, Русија, 31.8.2009 - 4.9.2009. „Springer“. стр. 26. ISBN 978-3-642-03274-5.
- ↑ Типичниот показател на прекршување на оптичко влакно се движи меѓу 1,518 и 1,538. Мидвинтер, Џ.Е. (1991). „Оптички влакна за пренос“ (второ издание. изд.). „Krieger Publishing Company“. ISBN 0-89464-595-1.
- ↑ „„Теоретското спроти реалното ограничување на брзината на Пинг"“. „Royal Pingdom“. „Pingdom“. јуни 2007. Архивирано од изворникот на 2010-09-02. Посетено на 5 мај 2010.
- ↑ „„Четврти ден: Месечево обиколување 7, 8 и 9"“. „The Apollo 8 Flight Journal“. НАСА. Архивирано од изворникот на 2011-01-04. Посетено на 16 декември 2010.
- ↑ 76,0 76,1 Научен институт за вселенски телескопи (5 јануари 2010). "„Хабл ја откри „Неоткриената Земја“ на исконски галаксии“". Соопштение за печат.
- ↑ „„Литографија „Хаблово ултрадлабоко поле""“ (PDF). НАСА. Посетено на 4 февруари 2010.
- ↑ „„МАУ и астрономските единици мерки"“. Меѓународен астрономски сојуз. Посетено на 11 октомври 2010.
- ↑ Прочитајте понатаму во „„StarChild прашање на месецот за март 2000 година"“. „StarChild“. НАСА. 2000. Посетено на 22 август 2009.
- ↑ Дики, Џ.О.; и др. (јули 1994). „„Ласерска месечева локација: Наследство од Аполо програмата"“. „Science“. 265 (5171): 482–490. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305.
- ↑ Стендиш, Е.М. (февруари 1982). „„JPL планетарните ефемериди"“. „Celestial Mechanics“. 26 (2): 181–186. Bibcode:1982CeMec..26..181S. doi:10.1007/BF01230883.
- ↑ Бернер, Џ.Б.; Брајант, С.Х.; Кинмен, П.В. (ноември 2007). „„Мерењето на опсег како што е користено во Мрежата на длабоката вселена"“. „Proceedings of the IEEE“. 95 (11): 2202–2214. doi:10.1109/JPROC.2007.905128.
- ↑ „Time is money when it comes to microwaves“. „Financial Times“. 10 May 2013. Посетено на 25 April 2014.
- ↑ 84,0 84,1 84,2 „„Решение 1 од Седумнаесеттата генерална конференција на тегови и мери"“. Меѓународно биро за тегови и мери. 1983. Посетено на 23 август 2009.
- ↑ 85,0 85,1 Коен, И.Б. (1940). „„Ремер и првата определба на брзината на светлината (1676 година)"“. Isis. 31 (2): 327–79. doi:10.1086/347594.
- ↑ 86,0 86,1 86,2
„„Touchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences"“ (PDF). „Journal des sçavans“ (француски): 233–36. 1676.
Преведено во „„За движењето на светлината од М. Ремер"“. „Philosophical Transactions of the Royal Society“. 12 (136): 893–95. 1677. doi:10.1098/rstl.1677.0024. (Како што е репродуцирано во Хатон, Ц.; Шо, Г.; Пирсон, Р. (1809). „„За движењето на светлината од М. Ремер"“. „Филозофската размена на идеи на Кралското друштво во Лондон, од нивниот трет почеток во 1665 година, во 1800 година: Скратено“. 2. Лондон: Ц. и Р. Болдвин. стр. 397–98.)
Образложението објавено во „Journal des sçavans“ се засновало врз извештај кој Ремер го прочитал на Француската академија на науките во ноември 1676 година. (Cohen, 1940, p. 346). - ↑ 87,0 87,1 87,2 87,3 Бредли, Џ. (1729). „„За новооткриеното движење на неподвижните ѕвезди"“. „Philosophical Transactions“. 35: 637–660.
- ↑ Дафет-Смит, П. (1988). „Практична астрономија со вашиот калкулатор“. „Cambridge University Press“. стр. 62. ISBN 0-521-35699-7., Екстракт од стр. 62
- ↑ 89,0 89,1 {{Наведено списание|title=„Решение B2 за редефинирање на астрономската единица за должина“|url=https://www.iau.org/static/resolutions/IAU2012_English.pdf%7Cyear=2012%7Cpublisher=[[Меѓународен астрономски сојуз}}
- ↑ „Интернационален систем на единици мерки, додаток 2014: Ажурирање на осмото издание (2006) на SI брошурата“ (PDF). Меѓународно биро за тегови и мери. 2014. стр. 14.
- ↑ Меѓународно биро за тегови и мерки (2006), Меѓународен систем на мерни единици (SI) (PDF) (VIII. изд.), стр. 126, ISBN 92-822-2213-6 (англиски)
- ↑ Питјева, Е.В.; Стендиш, Е.М. (2009). „„Предлози за масите на трите најголеми астероиди, односот на масите на Земјата и Месечината и астрономската единица"“. „Celestial Mechanics and Dynamical Astronomy“. 103 (4): 365–372. Bibcode:2009CeMDA.103..365P. doi:10.1007/s10569-009-9203-8.
- ↑ 93,0 93,1 Работна група на МАУ за бројчени стандарди на фундаменталната астрономија. „„Моментални најдобри проценки на РГ на МАУ за НСФА"“. Воена поморска опсерваторија на САД. Архивирано од изворникот на 2009-12-08. Посетено на 25 септември 2009.
- ↑ „„Водич за должина за почетници на НФЛ"“. Национална физичка лабораторија, ВБ. Архивирано од изворникот на 2010-08-31. Посетено на 28 октомври 2009.
- ↑ 95,0 95,1 95,2 95,3 95,4 Гибс, П. (1997). „„Како се мери брзината на светлината?"“. „Usenet Physics FAQ“. Универзитет на Калифорнија „Риверсајд“. Посетено на 13 јануари 2010.
- ↑ Фаулер, М. „„Брзината на светлината"“. Универзитет на Вирџинија. Посетено на 21 јануари 2010.
- ↑ Кук, Џ.; Мартин, М.; Меккартни, Х.; Вилф, Б. (1968). „„Директната определба на брзината на светлината како општ физички лабораториски експеримент"“. „American Journal of Physics“. 36 (9): 847. Bibcode:1968AmJPh..36..847C. doi:10.1119/1.1975166.
- ↑ Аоки, К.; Мицуи, Т. (2008). „„Мал експеримент за директно мерење на брзината на светлината"“. „American Journal of Physics“. 76 (9): 812–815. arXiv:0705.3996. Bibcode:2008AmJPh..76..812A. doi:10.1119/1.2919743.
- ↑ Џејмс, М.Б.; Ормонд, Р.Б.; Сташ, А.Џ. (1999). „„Мерење на брзината на светлината за мирјадата"“. „American Journal of Physics“. 67 (8): 681–714. Bibcode:1999AmJPh..67..681J. doi:10.1119/1.19352.
- ↑ 100,0 100,1 100,2 100,3 100,4 Есен, Л.; Гордон-Смит, А.С. (1948). „„Брзината на ширење на електромагнетните бранови изведена со помош на резонантните честоти на цилиндричен шуплив резонатор"“. „Proceedings of the Royal Society of London A“. 194 (1038): 348–361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
- ↑ 101,0 101,1 Роза, Е.Б.; Дорси, Н.Е. (1907). „„Односот на електромагнетните и електростатичките единици мерки"“. Билтен на Бирото за стандарди. 3 (6): 433. Bibcode:1906PhRvI..22..367R. doi:10.1103/PhysRevSeriesI.22.367.
- ↑ Есен, Л. (1947). „„Брзина на електромагнетните бранови"“. „Nature“. 159 (4044): 611–612. Bibcode:1947Natur.159..611E. doi:10.1038/159611a0.
- ↑ 103,0 103,1 Есен, Л. (1950). „„Брзината на ширење на електромагнетните бранови изведена со помош на резонантните честоти на цилиндричен шуплив резонатор"“. „Proceedings of the Royal Society of London A“. 204 (1077): 260–277. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433.
- ↑ Штауфер, Р.Х. (април 1997). „„Наоѓање на брзината на светлината со колачиња од бел слез"“. „The Physics Teacher“. Американска асоцијација на наставници по физика. 35 (4): 231. Bibcode:1997PhTea..35..231S. doi:10.1119/1.2344657. Посетено на 15 февруари 2010.
- ↑ „„BBC Look East за брзината на светлината" (експеримент)“. BBC Norfolk website. BBC. Посетено на 15 февруари 2010.
- ↑ Детална дискусија за интерферометарот и неговата уптреба може да се наје во Воган, Џ.М. (1989). „Фабри-Перовиот интерферометар“. „CRC Press“. стр. 47, pp. 384–391. ISBN 0-85274-138-3.
- ↑ 107,0 107,1 Фрум, К.Д. (1958). „„Нова определба на брзината на електромагнетните бранви во слободниот простор"“. „Proceedings of the Royal Society of London“, серија A, математички и физички науки. Кралско друштво на Лондон. 247 (1248): 109–122. Bibcode:1958RSPSA.247..109F. doi:10.1098/rspa.1958.0172. JSTOR 100591.
- ↑ 108,0 108,1 Саливан, Д.Б. (2001). „„Брзината на светлината добиена преку директни мерења на честотата и брановата должина"“. Во Лајд, Д.Р. (уред.). „Век на извонредни достигнувања во мерењето, стандардите и технологијата“ (PDF). „CRC Press“. стр. 191–193. ISBN 0-8493-1247-7. Архивирано од изворникот (PDF) на 2009-08-13. Посетено на 2015-10-15.
- ↑ 109,0 109,1 109,2 Ивенсон, К.М.; и др. (1972). „„Брзината на светлината добиена преку директни мерења на честотата и брановата должина на метан-стабилизиран ласер"“. „Physical Review Letters“. 29 (19): 1346–49. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
- ↑ 110,0 110,1 Галилеј, Г. (1954) [1638]. „Дијалози за две нови науки“. Х. Кру, А. Десалвио. „Dover Publications“. стр. 43. ISBN 0-486-60099-8. Архивирано од изворникот на 2014-02-03. Посетено на 2015-10-15.
- ↑ 111,0 111,1 Бојер, К.Б. (1941). „„Рани проценки на брзината на светлината"“. „Isis“. 33 (1): 24. doi:10.1086/358523.
- ↑ 112,0 112,1 Фоши, Ренато; Леоне, Матео (2009), „„Галилео, мерење на брзината на светлината и времето на реакција"“ (PDF), „Perception“, 38: 1251–9[мртва врска]
- ↑ Магалоти, Лоренцо (2001) [1667], „Saggi di Naturali Esperienze fatte nell' Accademia del Cimento“ (дигитално издание. изд.), Фиренца: Институт и музеј на историјата на науката
- ↑ 114,0 114,1 Хајгенс, К. (1690). „Traitée de la Lumière“ (француски). Пјер ван дер Аа. стр. 8–9.
- ↑ Мајкелсон, A. A. (1927). „„Мерење на брзината на светлината меѓу Монт Вилсон и Монт Сан Антонио“. „The Astrophysical Journal“. 65: 1. Bibcode:1927ApJ....65....1M. doi:10.1086/143021.
- ↑ Сартон, Г. (1993). „Античката наука во златната ера на Грција“. „Courier Dover“. стр. 248. ISBN 0-486-27495-0.
- ↑ 117,0 117,1 117,2 Меккеј, Р.Х.; Олдфорд, Р.В. (2000). „„Научниот метод, статистичкиот метод и брзината на светлината"“. „Statistical Science“. 15 (3): 254–78. doi:10.1214/ss/1009212817.
- ↑ Гроус, С.Г. (1999). „„Огнот кој доаѓа од очите"“. „Neuroscientist“. 5: 58–49. doi:10.1177/107385849900500108.
- ↑ Хамарнех, С. (1972). „„Осврт: Хаким Мохамед рекол: „Ibn al-Haitham""“. „Isis“. 63 (1): 119. doi:10.1086/350861.
- ↑ 120,0 120,1 Лестер, П.М. (2005). „Визуелна комуникација: Слики со пораки“. „Thomson Wadsworth“. стр. 10–11. ISBN 0-534-63720-5.
- ↑ О’Конор, Џ.Џ.; Робертсон, Е.Ф. „„Абу Али ал-Хасан ибн ал-Хајтхам"“. Мектудорова архива на математичката историја. Универзитет на Сеинт Ендрјуз. Посетено на 12 јануари 2010.
- ↑ Ложине, Пјер (2005). „„Мерење: Зошто? Како? Што?"“ (PDF). „Активности на Осмата меѓународна конференција за предавање историја, филозофија, социологија и природни науки“. Архивирано од изворникот (PDF) на 2012-05-27. Посетено на 2015-10-15.
- ↑ О’Конор, Џ.Џ.; Робертсон, Е.Ф. „„Абу хан Мухамед ибн Ахмед ел-Бируни"“. Мектудорова архива на математичката историја. Универзитет на Сеинт Ендрјуз. Посетено на 12 јануари 2010.
- ↑ Линдберг, Д.К. (1996). „Роџер Бејкон и потеклото на „Перспектива во средновековието“: критика и англиски превод на Бејконовата „Перспектива“, со вовед и забелешки“. „Oxford University Press“. стр. 143. ISBN 0-19-823992-0.
- ↑ Линдберг, Д.К. (1974). „„Синтеза во оптиката во доцниот тринаесетти век"“. Во Едвард Грант (уред.). „Изворна книга за средновековната наука“. „Harvard University Press“. стр. 396. ISBN 978-0-674-82360-0.
- ↑ Маршал, П. (1981). „„Никол Оресме за природата, рефлексијата и брзината на светлината"“. „Isis“. 72 (3): 357–74 [367–74]. doi:10.1086/352787.
- ↑ Флоријан Кајори, „Историја на физиката и нејзините елементарни гранки: заедно со развојот на физичките лаборатории“ (1922)
- ↑ Карл Бенџамин Бојер, „Виножитото: Од мит до математика“ (1959)
- ↑ Њутн, И. (1704). „Prop. XI“. „Оптикс“. Текстот на „Prop. XI“ е идентичен во првото (1704) и второто (1719).
- ↑ Грано, П.; Асис, А.К.Т. (1994). „„Кирхоф за движењето на електрицитетот низ проводници"“ (PDF). „Apeiron“. 19: 19–25. Посетено на 21 октомври 2010.[мртва врска]
- ↑ Џордано, Николас Џ. (2009). „Физика за на факултет: толкување и врски“. „Cengage Learning“. стр. 787. ISBN 0-534-42471-6., Екстракт од стр. 787
- ↑ Бергман, Петер Габриел (1992). „Загатката на гравитацијата“. „Courier Dover Publications“. стр. 17. ISBN 0-486-27378-4., Екстракт од стр. 17
- ↑ Баис, Сандер (2005). „Равенките: икони на знаењето“. „Harvard University Press“. стр. 40. ISBN 0-674-01967-9., Extract of page 40
- ↑ О’Конор, Џ.Џ.; Робертсон, Е.Ф. (ноември 1997). „„Џејмс Кларк Максвел"“. Школа за математика и статистика, Универзитет на Сеинт Ендрјуз. Архивирано од изворникот на 2011-01-28. Посетено на 13 октомври 2010.
- ↑ Мајкелсон, А.А.; Морли, Е.В. (1887). „„За релативното движење на Земјата и луминоферозниот етер"“. „American Journal of Science“. 34: 333–345. doi:10.2475/ajs.s3-34.203.333.
- ↑ Френч, А.П. (1983). „Специјална релативност“. „Van Nostrand Reinhold“. стр. 51–57. ISBN 0-442-30782-9.
- ↑ Даригол, О. (2000). „Електродинамиката од Ампер до Ајнштајн“. „Clarendon Press“. ISBN 0-19-850594-9.
- ↑ Галисон, П. (2003). „Ајнштајновите часовници, Поенкареовите мапи: Империи на времето“. „W.W. Norton“. ISBN 0-393-32604-7.
- ↑ Милер, А.И. (1981). „Специјалната теорија за релативноста на Алберт Ајнштајн: Појава (1905) и првични толкувања (1905–1911)“. „Addison–Wesley“. ISBN 0-201-04679-2.
- ↑ Пајс, А. (1982). „Господарот е префинет: Науката и животот на Алберт Ајнштајн“. „Oxford University Press“. ISBN 0-19-520438-7.
- ↑ „„Решение 6 од Петнаесеттата генерална конференција на тегови и мери"“. Меѓународно биро за тегови и мери. 1967. Посетено на 13 октомври 2010.
- ↑ Баргер, Р.; Хол, Џ. (1973). „„Брановата должина на 3.39-μm ласерски-заситена апсорпциона линија на метанот"“. „Applied Physics Letters“. 22 (4): 196. Bibcode:1973ApPhL..22..196B. doi:10.1063/1.1654608.
- ↑ „„Решение 6 од Петнаесеттата генерална конференција на тегови и мери"“. Меѓународно биро за тегови и мери. 1975. Посетено на 9 септември 2009.
- ↑ Тејлор, Е.Ф.; Вилер, Џ.А. (1992). „Физика на време-просторот: Вовед во специјалната релативност“ (второ издание. изд.). „Macmillan Publishers“. ISBN 0-7167-2327-1.
- ↑ Пензес, В.Б. (2009). „„Хронологија на дефиницијата на метарот"“ (PDF). НИСТ. Посетено на 11 јануари 2010.
- ↑
Адамс, С. (1997). „Релативност: Вовед во физиката на време-просторот“. „CRC Press“. стр. 140. ISBN 0-7484-0621-2.
„Необична последица на овој систем дефиниции е што никакво идно подобрување на нашите можности за мерење на c нема да ја промени брзината на светлината (дефиниран број), туку само должината на метарот!“
- ↑
Риндлер, В. (2006). „Релативност: специјална, општа и космолошка“ (второ издание. изд.). „Oxford University Press“. стр. 41. ISBN 0-19-856731-6.
„Забележете дека ... секакви унапредувања на експерименталната точност ќе го променат метарот во однос на атомските бранови должини, но не и вредноста на брзината на светлината!“
- ↑ „Формуалација на „експлицитната константа“, Меѓународно биро за тегови и мери, 2011
Литература[уреди | уреди извор]
Историски наводи[уреди | уреди извор]
- Ремер, О. (1676). „„Демонстрација во врска со движењето на светлината" („Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences")“. „Journal des sçavans“ (француски): 223–36. Архивирано од изворникот на 2007-07-29. Посетено на 2015-10-15.
- Халеј, Е. (1694). „„Господинот Касини, неговите нови и точни табели за затемнувањата на првиот сателит на Јупитер, редуцирани на меридијанот на Лондон“. „Philosophical Transactions of the Royal Society“. 18 (214): 237–56. doi:10.1098/rstl.1694.0048.
- Физо, Х.Л. (1849). „„За експеримент поврзан со брзината на ширење на светлината" („Sur une expérience relative à la vitesse de propagation de la lumière")“ (PDF). „Comptes rendus de l'Académie des sciences“ (француски). 29: 90–92, 132. Архивирано од изворникот на 2011-06-13. Посетено на 2015-10-15.CS1-одржување: бот: непознат статус на изворната URL (link)
- Фуко, Ж.Л. (1862). „„Експериментална определба на брзината на светлината: паралакса на Сонцето" („Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil")“. „Comptes rendus de l'Académie des sciences“ (француски). 55: 501–503, 792–796.
- Мајкелсон, А.А. (1878). „„Експериментална определба на брзината на светлината"“. „Proceedings of the American Association of Advanced Science“. 27: 71–77.
- Мајкелсон, А.А.; Пиз, Ф.Г.; Пирсон, Ф. (1935). „„Мерење на брзината на светлината во делумен вакуум"“. „Astrophysical Journal“. 82: 26–61. Bibcode:1935ApJ....82...26M. doi:10.1086/143655.
- Њуком, С. (1886). „„Брзината на светлината"“. „Nature“. 34 (863): 29–32. Bibcode:1886Natur..34...29.. doi:10.1038/034029c0.
- Перотин, Ж. (1900). „„За брзината на светлината" („Sur la vitesse de la lumière")“. „Comptes rendus de l'Académie des sciences“ (француски). 131: 731–4.
Современи наводи[уреди | уреди извор]
- Брилуен, Л. (1960). „Ширење на брановите и групна брзина“. „Academic Press“.
- Џексон, Џ.Д. (1975). „Класична електродинамика“ (второ издание. изд.). „John Wiley & Sons“. ISBN 0-471-30932-X.
- Кајзер, Г. (2000). „Комуникација преку оптички влакна“ (трето издание. изд.). „McGraw-Hill“. стр. 32. ISBN 0-07-232101-6.
- Нг., Ј.Џ. (2004). „„Феноменологија на квантна пена и квантна гравитација"“. Во Г. Амелино-Камелија; Џ. Ковалски-Гилкман (уред.). „Ефект на Планкова скала во астрофизиката и космологијата“. „Springer“. стр. 321ff. ISBN 3-540-25263-0.
- Хелмке Ј.; Риле Ф. (2001). „„Физиката зад дефиницијата на метарот"“. Во Т.Џ. Квин; С. Лешиута; П. Тавела (уред.). „Неодамнешен напредок во метрологијата и фундаменталните константи“. „IOS Press“. стр. 453. ISBN 1-58603-167-8.
Надворешни врски[уреди | уреди извор]
- „Тестирање на брзината на светлината во вакуумска цевка долга една милја“ „Popular Science Monthly“, септември 1930, стр. 17–18.
- Дефиниција на метарот (Меѓународно биро за тегови и мери, BIPM)
- Брзината на светлината во вакуум (Национален институт на стандарди и технологија, NIST)
- Галерија на податоци: Мајкелсонова брзина на светлината
- Subluminal Архивирано на 15 јуни 2005 г. (Java апликација која ги прикажува граничните вредности на информации при групна брзина)
- De Mora Luminis
- Дискусија за собирање светлосни брзини
- Брзина на светлината Архивирано на 15 јануари 2008 г. (катедра за физика на Универзитетот на Колорадо)
- c: Брзина на светлината (Шеесет симболи, катедра за физика на Универзитетот во Нотингам [видео])
- Usenet Physics FAQ (Често поставувани прашања во физиката)
- Илустрација на брзината на светлината
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Статијата „Брзина на светлината“ е избрана статија. Ве повикуваме и Вас да напишете и предложите избрана статија (останати избрани статии). |



