Електричен капацитет
Симболи | C |
|---|---|
| SI-единица | фарад |
| Електромагнетизам |
|---|
 |
'Капацитетот' е односот на промената на електричниот полнеж во системот со соодветната промена на неговиот електричен потенцијал. Постојат две тесно поврзани сродства за капацитетот: само капацитет и меѓусебен капацитет . Секој објект што може да биде електрично наполнет, покажува само капацитет . Материјал со голема само-капацитивност има повеќе електрично полнење при даден напон од оној со ниска капацитивност. Идејата за меѓусебен капацитет е особено важна за разбирање на операциите на кондензатор, една од трите елементарни линеарни електронски компоненти (заедно со отпорници и намотки).
Капацитетот е функција само на геометријата на дизајнот (на пример, површината на плочите и растојанието меѓу нив) и на диелектрик материјалот помеѓу плочите на кондензаторот. За многу диелектрични материјали, еластичноста, а со тоа и капацитивноста, е независна од потенцијалната разлика помеѓу проводниците и вкупниот полнеж на нив.
Единицата на капацитивност SI е фарад (симбол: F), именувана по англискиот физичар Мајкл Фарадеј. Кондензатор од 1 фарад имаме кога електричен полнеж од 1 кулон, има потенцијална разлика од 1 волт помеѓу неговите плочи. .[1] Реципрочниот капацитет се нарекува еластичност.
Самокапацитивност[уреди | уреди извор]
Во електричните кола, терминот капацитет е обично кратенка за меѓусебен капацитет помеѓу два соседни спроводници, како што се двете плочи на кондензаторот. Меѓутоа, за изолиран проводник постои и својство наречено "само-капацитивност", што е количина на електрично полнење што мора да се додаде во изолиран проводник за да се подигне нејзиниот електричен потенцијал од една единица (т.е. еден волт, во повеќето системи за мерење).[2] Референтна точка за овој потенцијал теоретски е спроводливост во шуплива сфера, на бесконечен полупречник, со проводник поставен во оваа сфера.
Математички, "само-капацитивност" на проводник е дефиниран од
кад
- q е полнењето што го има проводникот,
- dS е бесконечно мал елемент од областа,
- r е должината од dS до фиксната точка M во рамките на плочата.
Користејќи го овој метод, само-капацитивност на спроводливата сфера со полупречник R е:[3]
Пример вредностите на само-капацитивност се:
- за врвот "плоча" на генераторот на ван де Грааф, обична сфера од 20 cm во полупречник: 22.24 pF,
- планета Земјата: околу 710 μF.[4]
Мешавина од капацитет на намотка понекогаш се нарекува само-капацитивност,[5], но ова е различен феномен. Тоа е всушност меѓусебен капацитет помеѓу поединечните вртења на намотката и е форма на скитник, или паразитски кондензатор. Оваа само- капацитивност е важен фактор при високи честоти: ја менува пречка на намотката и доведува до паралелна резонанца резонанца. Во многу апликации ова е непожелен ефект и поставува граница на горната честота за правилно функционирање на колото.
Заемна капацитивност[уреди | уреди извор]
Честа форма е паралелната-плоча кондензатор, кој се состои од две проводни плочи изолирани едена од друга, обично со сендвич диелектрични материјали. Во паралелен кондензатор на плочи, капацитетот е многу близу пропорционален на површината на проводничките плочи и обратно пропорционален на растојанието помеѓу одделните плочи.
Ако полнењата на плочите се + q и - q , а V го дава напонот помеѓу плочите, тогаш капацитетот "C" е даден од
што дава напон / струја врска
Историски гледано, фарад се сметал за непријатно голема единица, електрично и физички. Неговите помали единици секогаш се користеле, тоа се микрофарад, нанофарад и пикофарад. Во поново време, технологијата напредуваше така што кондензаторите од 1 фарад и поголем (т.н. "суперкондензатори") може да се конструираат во структура малку поголема од монета батерија. Ваквите кондензатори главно се користат за складирање на енергија за замена на традиционалните батерии.
Енергијата складирана во кондензаторот се пресметува со интеграција на работата W :
Mатрица за капацитет[уреди | уреди извор]
Горенаведената дискусија е ограничена на случајот на две спроводни плочи, иако на произволна големина и форма. Дефиницијата не се применува кога има повеќе од две наполнети плочи, или кога нето полнењето на двете плочи не е нула. За да се справи со овој случај, Максвел ги претставил своите "коефициенти на потенцијалот". Ако на три (речиси идеални) проводници се даваат полнења , тогаш напонот на проводникот 1 е даден со
и слично за другите напони. Херман фон Хелмхолц и Сер Вилијам Томсон покажаа дека коефициентите на потенцијалот се симетрични, така што , итн. Така системот може да биде опишан со збир на коефициенти познати како "матрица на еластичност" или "реципрочна матрица на капацитивност", која е дефинирана како:
Од ова, меѓусебните капацитети помеѓу два објекти можат да бидат дефинирани[6] со решавање за вкупниот полнеж Q и користејќи .
Бидејќи ниеден вистински уред не располага со совршено еднакви и спротивни полнења на секоја од двете "плочи", тоа е меѓусебната капацитивност што е пријавена на кондензаторите.
Колекцијата на коефициенти е позната како матрица на кондензатор ,[7][8] и е обратна на еластичната матрица.
Кондензатори[уреди | уреди извор]
Капацитетот на поголемиот дел од кондензаторите што се користат во електронските кола обично е за неколку редови помал од фарад. Најчестите подгрупи на капацитивност што се користат денес се: микро, фарад (μF), нанофарад (nF), пикофарад (pF), и, во микроколата, фемтофарад (fF). Сепак, специјално направените суперкондензатори може да бидат многу поголеми (како стотици фарадови), а паразитските капацитивни елементи може да бидат помали од фемтофарад. Во минатото, алтернативните подединици биле користени во историските електронски книги; "mfd" и "mf" за микрофарад (μF); "mmfd", "mmf", "μμF" за пикофарад (pF); но ретко се користат повеќе.[9][10]
Капацитивноста може да се пресмета ако се познати геометријата на проводниците и диелектричните својства на изолаторот помеѓу проводниците. Квалитативно објаснување за ова може да се даде на следниов начин. Откако ќе се стави позитивен полнеж на проводник, ова полнење создава електрично поле, отфрлајќи било кое друго позитивно полнење кое треба да се додаде кон проводникот; односно, зголемување на потребниот напон. Но, ако во близина има друг проводник со негативен полнеж, електричното поле на позитивниот проводник со одбивање на вториот позитивен полнеж е ослабен (вториот позитивен полнеж исто така ја чувствува привлечната сила на негативното полнење). Значи, поради вториот проводник со негативен полнеж, станува полесно да се стави позитивен полнеж на веќе позитивниот наполнет прв спроводник и обратно; односно потребниот напон е намален.
Како квантитативен пример, разгледај ја капацитивноста на кондензатор конструирана од две паралелни плочи и од областа А одделени со растојание d . Ако d е доволно мал во однос на најмалиот акорд на A , има високо ниво на точност:
каде
- C е капацитивност, во фаради;
- А е површина на преклопување на двете плочи, во квадратни метри;
- εr е релативна статичка променливост (понекогаш наречена диелектрична константа) на материјалот помеѓу плочите (за вакуум, εr = 1);
- ε0 is the електрична константа (ε0 ≈ 8,854⋅10-12 F.m-1); и
- d е одвојување помеѓу плочите, во метри;
Капацитетот е пропорционален на површината на преклопување и обратно пропорционална со одвојувањето помеѓу спроведните листови. Колку се поблиску листовите меѓусебно, толку е поголем капацитетот. Равенката е добра апроксимација ако d е помал во споредба со другите димензии на плочите, така што електричното поле во областа на кондензаторот е рамномерно, а таканареченото 'поле за полнење' околу периферијата обезбедува само мал придонес кон капацитетот. Во CGS единици равенката има форма:[11]
каде "C" во овој случај има единици на должина. Комбинирање на SI-равенката за капацитивност со горенаведената равенка за енергијата складирана во капацитет, за кондензатор со рамна плоча, складирана енергија е:
каде што W е енергијата, во џули; C е капацитивност, во фаради; и V е напонот, во волти.
Спречен капацитет[уреди | уреди извор]
Било кој два соседни проводници можат да функционираат како кондензатор, иако капацитетот е мал, освен ако проводниците не се блиску на големи растојанија или на голема површина. Овој (честопати несакан) капацитет се нарекува паразитски или "залутан капацитет". Залутаниот капацитет може да дозволи сигналите да истекуваат помеѓу поинаку изолираните кола (ефект наречен преслушување), и може да биде ограничувачки фактор за правилно функционирање на колата на висока честота.
Залутаниот капацитет помеѓу влезот и излезот во колото на засилувачот може да биде проблематичен бидејќи може да формира патека на повратни информации, што може да предизвика нестабилност и паразитски осцилации во засилувачот. Често е погодно за аналитички цели да се замени оваа капацитивност со комбинација на еден влез „заземјување“ на капацитивност и еден излез „заземјување“ на капацитивност; оригиналната конфигурација ( вклучувајќи ја и влез-кон-излезната капацитивност ) често се нарекува пи-конфигурација. Теоремата на Милер може да се искористи за да се изврши оваа замена: таа вели дека ако состојбата на степенот на два јазли е 1/K, тогаш импеданса на Z ги поврзува двата јазли може да се замени со импеданса на Z/(1 − K) помеѓу првиот јазол и земјата и KZ/(K − 1) импеданса помеѓу вториот јазол и земјата. Бидејќи импедансата варира обратно со капацитивноста, капацитетот на јазолот, C, се заменува со капацитивност на KC од влезот на земјата и капацитивноста (K − 1)C/K од излез на Земјата. Кога степенот на влезот-во-излез е многу голем, еквивалентната импеданса на влез-на-земјата е многу мала, додека импедансата излез-на-земја е во суштина еднаква на оригиналната импеданса (влез-излез).
Капацитет на кондензатори со едноставни облици[уреди | уреди извор]
За да се пресмета капацитетот на систем, се користи разрешената Лапласова равенка ∇2φ = 0 со постојан потенцијал φ на површината на спроводниците. Ова е безначајно кај случаите на висока симетрија. Кај посложените случаи не можат да се користат едноставни функции.
За дводимензионални ситуации аналитичките функции можат да се користат за да се определат различните геометрии споредбено. Погледајте Шварц–Кристофелово мапирање.
| Вид | Капацитет | Коментар |
|---|---|---|
| Пралелно плочест кондензатор | ||
| Коаксијален кабел | 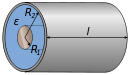
| |
| Пар на паралелни жици[12] | 
| |
| Жица паралелна на ѕид[12] | a: Пречник на жицата d: Растојание, d > a ℓ: Должина на жицата | |
| Две паралелни копланарни ленти[13] |
d: Растојание w1, w2: Ширина на лентата km: d/(2wm+d) k2: k1k2 | |
| Концентрични топки | 
| |
| Две топки, со ист полупречник[14][15] |
a: Полупречник d: Растојание, d > 2a D = d/2a, D > 1 γ: Ојлерова константа | |
| Топка пред ѕид[14] | a: Полупречник d: Растојание, d > a D = d/a | |
| Топка | a: Полупречник | |
| Кружен диск[16] | a: Полупречник | |
| Сфероид[17] | полуоски a>b=c | |
| Тенка права жица со конечна должина[18][19][20] |
a: Полупречник ℓ: Должина Λ: ln(ℓ/a) |
Складирање на енергија[уреди | уреди извор]
Енергијата (мерено во joule и) зачувана во кондензатор е еднаква на работата потребна за да ги притисне полнењата во кондензаторот, т.е. да ја наполните. Размислете, капацитетот на кондензаторот C , држејќи полнеж + q на една плоча и - q од друга страна. Преместувањето на мал елемент на полнење од 'q' 'од една плочка на друга, спротивно на потенцијалната разлика, бара {{работа "d"} {V} =} q / C' '}}} 'W' ':
каде "W" е делот што се мери во џули, "q" е полнежот кој се мери во кулони, а "C" е капацитетот, мерен во фаради.
Енергијата складирана во кондензаторот се пресметува со integrating оваа равенка. Почнувајќи со неоптоварената капацитивност ( q = 0) и движењето на полнењето од една плоча до друга, додека плочките имаат + Q и - Q ' ' е = на бараната работа' 'W' ':
Нанометри системи[уреди | уреди извор]
Капацитетот на наномасните диелектрични кондензатори како што се квантни точки може да се разликува од конвенционалните формулации на поголемите кондензатори. Особено, разликата во електростатичкиот потенцијал кај електроните во конвенционалните кондензатори е просторно дефинирана и фиксирана од формата и големината на металните електроди, покрај статистички голем број на електрони присутни во конвенционалните кондензатори. Меѓутоа, кај нанокрилните кондензатори, електростатичките потенцијали што ги воочиле електроните се одредуваат според бројот и локациите на сите електрони кои придонесуваат за електронските својства на уредот. Во такви уреди, бројот на електрони може да биде многу мал, меѓутоа, резултирачката просторна распределба на еквипотенцијалните површини во уредот е премногу сложена.
Единечни електронски уреди[уреди | уреди извор]
Капацитетот на поврзан, или "затворен" единствен електронски уред е двапати поголем од капацитетот на неповрзан, или "отворен", единствен електронски уред.[21] Овој факт може да се следи пофундаментално преку енергијата складирана во еден електронски уред чија интеракција на "директна поларизација" може подеднакво да се подели на интеракцијата на електронот со поларизиран полнеж на самиот уред поради присуството на електронот и количината на потенцијалната енергија потребна за да се формира поларизирано полнење на уредот (интеракцијата на полнежот во диелектричниот материјал на уредот со потенцијалот што се должи на електронот).[22]
Неколку електронски уреди[уреди | уреди извор]
Деривацијата на "квантната капацитивност" на уредот со неколку електрони го вклучува термодинамичкиот хемиски потенцијал на системот "N" - честички даден од
чии енергетски термини можат да се добијат како решенија на Schr & ouml; со провлекување на равенството. Дефиницијата на капацитетот,
- ,
со потенцијална разлика
може да се примени на уредот со додавање или отстранување на поединечни електрони,
- and .
Потоа
е "квантен капацитет" на уредот.[23]
Овој израз на "квантен капацитет" може да биде напишан како
што се разликува од конвенционалниот израз опишан во воведот, каде што , складираната електростатичка потенцијална енергија,
со фактор 1/2 со .
Меѓутоа, во рамките на чисто класичните електростатички интеракции, појавата на факторот 1/2 е резултат на интеграција во конвенционалната формулација,
што е соодветно бидејќи за системи кои вклучуваат или многу електрони или метални електроди, но во неколку електронски системи, . Интегралот генерално станува сумација. Еден може тривиjјално да ги комбинира изразите на капацитетот и енергијата на електростатичка интеракција,,
- and ,
соодветно, за да се добие,
што е слично на квантната капацитивност. Поригорозната деривација е пријавена во литературата.[24] Особено, за да ги заобиколат математичките предизвици на просторно сложените еквипотенцијални површини во рамките на уредот, просечното електростатичко потенцијално искуство од секој електрон се користи во деривацијата.
Причината за очигледните математички разлики се разбира пофундаментално, бидејќи потенцијалната енергија на изолиран уред (само-капацитивност) е двапати поголема од складираната во "поврзаниот" уред во долната граница N = 1. Како N расте нагоре, .[22] Така, општото изразување на капацитетот е:
.
Во нано-уредите како што се квантните точки, "кондензаторот" е често изолирана или делумно изолирана компонента во уредот. Примарните разлики помеѓу кондензаторите на нанос и макроскопските (конвенционални) кондензатори се бројот на вишокот на електрони (носители на полнење или електрони кои придонесуваат за електронското однесување на уредот) и обликот и големината на металните електроди. Во нано-уреди, нанопроводниците кои се состојат од метални атоми обично не ги покажуваат истите проводни својства како нивните макроскопски или делови на материјал.
Капацитет во електронски и полупроводнички уреди[уреди | уреди извор]
Во електронските и полупроводничките уреди, транзиентната или честотно-зависна струја меѓу терминалите ги содржи и компонентите за спроводливост и поместување. Струјата на спроводливост е поврзана со носачи на носивост (електрони, дупки, јони, итн.), Додека струјата на поместување е предизвикана од електричното поле со различно време. Транспортот на превозникот е под влијание на електричното поле и од голем број на физички појави - како што се носење на носач и дифузија, заробување, инјектирање, ефекти поврзани со контактот, јонизација на удар, итн. Како резултат на тоа, уредот admittance е зависен од честотата , и едноставна електростатичка формула за капацитет не е применлива. Поопшта дефиниција на капацитетот, опфаќајќи електростатичка формула, е:[25]
каде е приемот на уредот, и е аголна честота.
Во принцип, капацитетот е функција на честота. На високи честоти, капацитетот се приближува кон константна вредност, еднаква на "геометриската" капацитивност, одредена со геометријата на терминалите и диелектричната содржина во уредот. Хартијата на Стивен Лаукс [25] претставува преглед на бројчени техники за пресметка на капацитетот. Особено, капацитетот може да се пресмета со Фуриева трансформација на транзиентна струја како одговор на скаларно напонско возбудување:
Негативна капацитивност во полупроводнички уреди[уреди | уреди извор]
Обично, капацитивноста во полупроводнички уреди е позитивна. Меѓутоа, во некои уреди и под одредени услови (температура, применливи напони, честота, итн.), Капацитетот може да стане негативен. Немонотонското однесување на транзиентната струја како одговор на чекор-како возбуда е предложено како механизам на негативен капацитет.[26] Негативната капацитивност е демонстрирана и истражена во многу различни типови на полупроводнички уреди.[27]
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ http://www.collinsdictionary.com/dictionary/english/farad
- ↑ William D. Greason (1992). Electrostatic discharge in electronics. Research Studies Press. стр. 48. ISBN 978-0-86380-136-5. Посетено на 4 December 2011.
- ↑ Lecture notes; University of New South Wales
- ↑ Tipler, Paul; Mosca, Gene (2004), Physics for Scientists and Engineers (5. изд.), Macmillan, стр. 752, ISBN 978-0-7167-0810-0
- ↑ Massarini, A.; Kazimierczuk, M.K. (1997). „Self-capacitance of inductors“. IEEE Transactions on Power Electronics. 12 (4): 671–676. doi:10.1109/63.602562.: example of the use of the term 'self-capacitance'
- ↑ Jackson, John David (1999), Classical Electrodynamic (3.. изд.), USA: John Wiley & Sons, Inc., стр. 43, ISBN 978-0-471-30932-1
- ↑ Maxwell, James (1873), A treatise on electricity and magnetism, Volume 1, 3, Clarendon Press, стр. 88ff
- ↑ „Capacitance“. Посетено на 20 September 2010.
- ↑ Capacitor MF-MMFD Conversion Chart; Just Radios.
- ↑ Fundamentals of Electronics - Volume 1b - Basic Electricity - Alternating Current; Bureau of Naval Personnel; 1965; page 197.
- ↑ The Physics Problem Solver, 1986, Google books link
- ↑ 12,0 12,1 Jackson, J. D. (1975). Classical Electrodynamics. Wiley. стр. 80.
- ↑ Binns; Lawrenson (1973). Analysis and computation of electric and magnetic field problems. Pergamon Press. ISBN 978-0-08-016638-4.
- ↑ 14,0 14,1 Maxwell, J. C. (1873). A Treatise on Electricity and Magnetism. Dover. стр. 266ff. ISBN 0-486-60637-6.
- ↑ Rawlins, A. D. (1985). „Note on the Capacitance of Two Closely Separated Spheres“. IMA Journal of Applied Mathematics. 34 (1): 119–120. doi:10.1093/imamat/34.1.119.
- ↑ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. стр. 128, problem 3.3.
- ↑ Howard C., Berg (1993). Random walks in biology (Expanded. изд.). Princeton, N.J.: Princeton University Press. ISBN 0691000646. OCLC 27810154.
- ↑ Maxwell, J. C. (1878). „On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness“. Proc. London Math. Soc. IX: 94–101. doi:10.1112/plms/s1-9.1.94.
- ↑ Vainshtein, L. A. (1962). „Static boundary problems for a hollow cylinder of finite length. III Approximate formulas“. Zh. Tekh. Fiz. 32: 1165–1173.
- ↑ Jackson, J. D. (2000). „Charge density on thin straight wire, revisited“. Am. J. Phys. 68 (9): 789–799. Bibcode:2000AmJPh..68..789J. doi:10.1119/1.1302908.
- ↑ Raphael Tsu (2011). Superlattice to Nanoelectronics. Elsevier. стр. 312–315. ISBN 978-0-08-096813-1.
- ↑ 22,0 22,1 T. LaFave Jr. (2011). „Discrete charge dielectric model of electrostatic energy“. J. Electrostatics. 69 (6): 414–418. arXiv:1203.3798. doi:10.1016/j.elstat.2011.06.006.
- ↑ G. J. Iafrate; K. Hess; J. B. Krieger; M. Macucci (1995). „Capacitive nature of atomic-sized structures“. Phys. Rev. B. 52 (15). Bibcode:1995PhRvB..5210737I. doi:10.1103/physrevb.52.10737.
- ↑ T. LaFave Jr; R. Tsu (март–април 2008). „Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons“ (PDF). Microelectronics Journal. 39 (3–4): 617–623. doi:10.1016/j.mejo.2007.07.105. Архивирано од изворникот (PDF) на 22 февруари 2014. Посетено на 12 февруари 2014.
- ↑ 25,0 25,1 S. E. Laux, "Techniques for small-signal analysis of semiconductor devices", IEEE Trans. Computer-Aided Design, vol. CAD-4, pp. 472-481, 1985.
- ↑ A. K. Jonscher, "The physical origin of negative capacitance", J. Chem. Soc. Faraday Trans. II, vol. 82, pp. 75-81, 1986.
- ↑ М. Ершов, Х. Ц. Лиу, Л. Ли, М. Буканан, З. Р. Василевски, А. К. Јоншер, "Негативен ефект на кондензатор во полупроводнички направи", IEEE Trans. Electron Devices, vol. 45, no. 10, pp. 2196-2206, Oct. 1998.
Дополнителна литература[уреди | уреди извор]
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Electricity and Magnetism, Light (4th ed.). W. H. Freeman. ISBN 1-57259-492-6
- Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6 ed.). Brooks Cole. ISBN 0-534-40842-7
- Saslow, Wayne M.(2002). Electricity, Magnetism, and Light. Thomson Learning. ISBN 0-12-619455-6. See Chapter 8, and especially pp. 255–259 for coefficients of potential.
































![{\displaystyle {\frac {2\pi \varepsilon \ell }{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19746fa861b22587cd9fbfcc0ed075187e6dc6a)























![{\displaystyle C(\omega )=1/(\Delta V)\int _{0}^{\infty }[i(t)-i(\infty )]cos(\omega t)dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ae46997077cb3776ef3946fcc54a8bd0e56d58c)