Брзина

Брзина
Како се менува насоката, додека автомобилите се на кружна патека, и нивната брзина се менува, не е константна.
Симболи	v, v
SI-единица	м/с

Брзина — стапката на промена на положбата во однос на појдовниот систем, и претставува функција од времето. Брзината е всушност утврдување на средната брзина и правецот на движење (на пример 60 км/ч на север). Брзина е важен концепт во кинематиката, дел од класичната механика кој го опишува движењето движење на телата.

Брзина е физичка вектор количина; и големината и насоката се потребни да ја дефинираат. скаларна апсолутна вредност (големина) на брзина се нарекува "брзина", добиена количина како една кохерентна единица која се мери во SI (метрички) систем метри во секунда (м/с) или SI база на (m⋅s⁻¹). На пример, "5 метри во секунда" е скаларна, додека "5 метри во секунда истична" е вектор.

Ако постои промена во брзината, насоката или и двете, тогаш објектот ја менува брзина и се вели дека е во процес на забрзување забрзување.

Постојана брзина спрема забрзување

За да имаат постојана брзина, објектите мора да има постојана брзина во постојана насока. Постојаната насока го ограничува објектот на движење по вистинскиот пат, на тој начин, постојана брзина значи движење во права линија со константна брзина.

На пример, автомобил кој се движи со константна брзина од 20 километри на час на кружна патека има постојана брзина, но нема постојана брзина, бидејќи неговата насока трпи промени. Оттука, автомобилот се смета дека е во процес на забрзување.

Равенка на движење

Главна статија: Равенка на движење

Просечната брзина

Брзина се дефинира како стапка на промена на својот став во однос на времето, која исто така може да биде наведена како моментална брзина за да се нагласи разликата од просечната брзина. Во некои апликации "просечната брзина" на објектот можеби ќе биде потребна, така да се каже, да ги обезбеди добиените поместување на постојаната брзина како променлива брзина во ист временски интервал, v (t), во текот на одреден временски период Δt . Просечната брзина може да се пресмета како:

${\boldsymbol {\bar {v}}}={\frac {\Delta {\boldsymbol {x}}}{\Delta {\mathit {t}}}}.$

Просечната брзина е секогаш помала или еднаква на просечната брзина на објектот. Ова може да се види при реализирање, додека растојанието секогаш строго се зголемува, поместувањето може да се зголеми или намали, сè додека ја менува својата насока.

Во смисла на зафатнина работно време (x vs. t) Графика, моментална брзина (или, едноставно, брзина) може да се смета за наклонот на тангентата на кривата на која било точка, а просечната брзина како патека на секанс линија помеѓу две точки, т координира еднаква на границите на рокот за просечната брзина.

Просечната брзина е иста како и на брзината на просечното време - може да се каже, просечно броено време , кое може да се пресмета како време составено во брзината:

${\boldsymbol {\bar {v}}}={1 \over t_{1}-t_{0}}\int _{t_{0}}^{t_{1}}{\boldsymbol {v}}(t)\ dt,$

каде што може да се идентификуваат

$\Delta {\boldsymbol {x}}=\int _{t_{0}}^{t_{1}}{\boldsymbol {v}}(t)\ dt$

и

$\Delta t=t_{1}-t_{0}.$

Mоментална брзина

Графички приказ на брзина во однос на времето, како и односот помеѓу брзината V на y-оската, забрзувањето a (трите зелени тангентни линии претставуваат вредностите за забрзување на различни точки по должината на кривата) и поместување s (жолта површина под сината крива.)

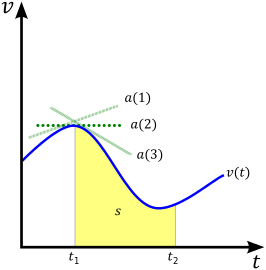
Ако ги земеме предвид V како брзина и X како поместување (промена на позиција) вектор, тогаш може да ја искажат (моменталната) брзината на честички или објекти, во секое посебно време t, како производ на позицијата во однос на времето

${\boldsymbol {v}}=\lim _{{\Delta t}\to 0}{\frac {\Delta {\boldsymbol {x}}}{\Delta t}}={\frac {d{\boldsymbol {x}}}{d{\mathit {t}}}}.$

Од овој производ на равенка, во едно-димензионален случај може да се види дека на тоа подрачје во рамките на брзината во однос на времето (v vs. t график) е поместување, х. Во смисла на анализата , интеграл на функцијата брзина В (t) е поместувањето функција x (T). Во бројка, тоа одговара на жолтата површината под кривата означена со s (s е алтернативна нотација за поместување).

${\boldsymbol {x}}=\int {\boldsymbol {v}}\ d{\mathit {t}}.$

Од производот на позицијата во однос на времето која дава промена во позицијата (во метри) поделено со промена на време (во секунди), брзината се мери во метри во секунда (м/с). Иако концептот на моментална брзина може се на прв поглед да изгледа контра-интуитивно, може да се смета за брзината, дека објектот ќе продолжи да се движи и ако престанува забрзување во тој момент.

Односи на забрзувањето

Иако брзинаta се дефинира како стапка на промена на позицијатa, тоа вообичаено може да се започне со изразот на објектот за забрзување . Како што се гледа од сликата на трите зелени линии на сликата, моменталното забрзување на објектот во една точка во времето на патеката на тангентата на кривата на (Предлошка:Математика Предлошка:Наспроти математика графиконот во тој момент, со други зборови, забрзувањето се дефинира како дериват на брзината во однос на времето.:

${\boldsymbol {a}}={\frac {d{\boldsymbol {v}}}{d{\mathit {t}}}}.$

Од таму, може да се добие израз за брзина како област на забрзување во однос на времето (Предлошка:Математика Предлошка:Наспроти математика) графиконот. Како и погоре, ова е направено со помош на концептот на интеграли:

${\boldsymbol {v}}=\int {\boldsymbol {a}}\ d{\mathit {t}}.$

Постојано забрзување

За посебен случај на постојана забрзување, брзина може да се изучува со користење на равенки на движење. Со оглед на 'на' за еднакви со некои произволни постојана вектор, лесно е да се покаже дека

${\boldsymbol {v}}={\boldsymbol {u}}+{\boldsymbol {a}}t$

со v како брзина на времето t и u као забрзување во време t = 0. Со комбинирање на оваа раенка со равенката x = ut + at²/2, можно е да се прикажат поместувањата и просечната брзина со

${\boldsymbol {x}}={\frac {({\boldsymbol {u}}+{\boldsymbol {v}})}{2}}{\mathit {t}}={\boldsymbol {\bar {v}}}{\mathit {t}}$.

Исто така е можно да се изведе израз за независна брзината на време, познат како торикели равенка, како што следува:

$v^{2}={\boldsymbol {v}}\cdot {\boldsymbol {v}}=({\boldsymbol {u}}+{\boldsymbol {a}}t)\cdot ({\boldsymbol {u}}+{\boldsymbol {a}}t)=u^{2}+2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}$

$(2{\boldsymbol {a}})\cdot {\boldsymbol {x}}=(2{\boldsymbol {a}})\cdot ({\boldsymbol {u}}t+{\frac {1}{2}}{\boldsymbol {a}}t^{2})=2t({\boldsymbol {a}}\cdot {\boldsymbol {u}})+a^{2}t^{2}=v^{2}-u^{2}$

$\therefore v^{2}=u^{2}+2({\boldsymbol {a}}\cdot {\boldsymbol {x}})$

каде што v = |v| и др.

Горенаведените равенки важат и за Њутновата механика и специјалната релативност. Каде Њутновата механика и специјалната релативност се разликуваат во тоа како различни набљудувачи би ја опишале иста ситуација. Конкретно, во Њутновата механика, сите експерти се согласуваат вредноста на t при правилно трансформирање на позиција да се создаде ситуација во која не-забрзувањето сите набљудувачи би го опишале забрзувањето на објектот со истите вредности. Ниту едно не е точно за специјалената релативност. Со други зборови, само релативната брзината може да се пресмета.

Количините кои се зависни од брзината

Кинетичката енергија на движење на објект зависи од неговата брзина и е дадена со равенката

$E_{\text{k}}={\tfrac {1}{2}}mv^{2}$

занемарувајќи ја специјална релативност, каде што E_k е кинетичка енергија и m е масата. Кинетичка енергија е производ што зависи од квадратот на брзината, поврзани со количеството, интензитетот, е вектор и е утврдено со:

${\boldsymbol {p}}=m{\boldsymbol {v}}$

Кај специјалната релативност, бездимензионалниот Лоренц Фактор се појавува често, и е дадена со

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

каде γ е фактор Лоренц и C е брзината на светлината.

Излезна брзина е минималната брзина на балистички објект кој треба да излезе од масивно тело како Земјата. Тоа претставува кинетичката енергија што, кога се додава на гравитациска потенцијална енергија на објектот, (кој е секогаш негативен) е еднаков на нула. Општата формула за излезна брзина на објект од далечина R од центарот на планета со маса "'M' 'е:

$v_{\text{e}}={\sqrt {\frac {2GM}{r}}}={\sqrt {2gr}},$

каде што G е гравитациска константа и g е гравитациското забрзување. Излезната брзина од површината на Земјата е околу 11 200 м/с, и без разлика на насоката на објектот.

Релативна брзина

Главна статија: Релативна брзина

Релативна брзина е мерење на брзина помеѓу два предмети кои се определени (поставени) во еден координатен систем. Релативната брзина е од фундаментално значење во класичната и современата физика, бидејќи многу системи во физиката се поврзани со релативно движење на два или повеќе предмети. Во Њутновата механика, релативната брзина е независна од избраниата внатрешна референтна рамка. Ова не е случај со специјалната релативност кај која брзината зависи од изборот на референтна рамка.

Ако предметот A се движи со брзина вектор v и предметот B со вектор на брзината w, тогаш брзината на предметот A во однос на предметот B е дефиниран како разлика на двете брзини помеѓу векторите:

${\boldsymbol {v}}_{A{\text{ relative to }}B}={\boldsymbol {v}}-{\boldsymbol {w}}$

Слично на релативната брзина на предметот B кој се движи со брзина w, во однос на предметот A кој се движи со брзина v е:

${\boldsymbol {v}}_{B{\text{ relative to }}A}={\boldsymbol {w}}-{\boldsymbol {v}}$

Обично внатрешната рамка во која се избрани двата споменати предмети е во мирување.

Скаларни брзини

Во едно димензионалните случиаи, брзините се скалари и равенката е:

$\,v_{rel}=v-(-w)$, ако двата објекти се движат во спротивни насоки, или:

$\,v_{rel}=v-(+w)$, ако двата предмети се движат во иста насока.

Поларни координати

Во поларни координати, две-димензионалната брзина е опишана од страна на радијалната брзина, дефинирана како компонента на брзина далеку од или кон основата (исто така познат како velocity made good), или како аголна брзина, за која вредност на ротацијата на основата (со позитивни вредности претставува ротација во спротивен правец на стрелките на часовникот, а со негативни количини претставува ротација во правец на стрелките на часовникот, во десен координатен систем).

Радијалната и аголната брзина може да се добијат од Декартовата брзина и поместување на векторите со разложување на векторот на брзината во радијални и попречни компоненти. Попречните брзини се компонента на брзината долж кругот поставен на основата.

${\boldsymbol {v}}={\boldsymbol {v}}_{T}+{\boldsymbol {v}}_{R}$

каде

${\boldsymbol {v}}_{T}$ е попречна брзина

${\boldsymbol {v}}_{R}$ е радијална брзина.

Големината на радијалната брзина е производ на векторот на брзината и на едининечен вектор во насока на поместувањето.

$v_{R}={\frac {{\boldsymbol {v}}\cdot {\boldsymbol {r}}}{\left|{\boldsymbol {r}}\right|}}$

каде

${\boldsymbol {r}}$ е поместување.

Големината на попречната брзина е производ на единечен вектор во насока на поместување и векторот на брзината. А исто така е и производ на аголна брзина $\omega$ и големината на поместување.

$v_{T}={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|}}=\omega |{\boldsymbol {r}}|$

така што

$\omega ={\frac {|{\boldsymbol {r}}\times {\boldsymbol {v}}|}{|{\boldsymbol {r}}|^{2}}}.$

Аголниот момент во скаларен облик претставува временската дистанца до основното време на попречната брзина, или еквивалентно, на временското растојание на аголната брзина на квадрат. Знакот за аголниот момент е ист како и за аголна брзина.

$L=mrv_{T}=mr^{2}\omega \,$

каде

$m\,$ е маса

$r=\|{\boldsymbol {r}}\|.$

Изразот $mr^{2}$ познат како момент на инерција. Ако силите во радијалната насока се со обратна квадратна зависност, како и во случај на гравитациа во орбитата, аголниот момент е постојан, а попречната брзината е обратно пропорционална на далечината, додека аголната брзина е обратно пропорционална на далечина на квадрат, и вредноста чија област на поместување е постојана. Овие односи се познати како законите на Кеплер за планетарното движење.

Поврзано

• Четири-брзина
• Групна брзина
• Хипербрзина
• Фазна брзина
• Сопствена брзина
• Брзиност
• Конечна брзина

Наводи

• Robert Resnick and Jearl Walker, Fundamentals of Physics, Wiley; 7 Sub edition (June 16, 2004). ISBN 0-471-23231-9.

Надворешни врски

• Брзина на Ризницата
• physicsabout.com Архивирано на 25 мај 2021 г., Speed and Velocity
• Velocity and Acceleration
• Introduction to Mechanisms (Carnegie Mellon University)