Кружно движење
| Класична механика |
|---|
Во физиката, кружно движење е движење на објектот по обемот на кругот или ротација по кружна патека. Тоа може да е рамномерно, со константна аголна стапка на ротација и постојана брзина, или не-рамномерно со менување на стапката на ротација. Ротација околу фиксна оска на три-димензионални тело вклучува кружни движења на неговите делови. Равенките на движење опишува движење на центарот на маса на телото.
Примери на кружни движења вклучуваат: вештачки сателити кои кружат околу Земјата во постојана висина, а тавански вентилаторски ножеви ротираат околу еден центар, камен кој е врзан за јаже и се нишаше во кругови, автомобил, вртење преку крива во тркачка патека, електрон се движи нормално на рамномерно магнетно поле, и опрема која се движи внатре во механизамот.
Предметот со вектор на брзина постојано ја менува насоката на движење, предметот во движење е во процес на акцелерација со центрипетална сила во насока на центарот на ротација. Без оваа забрзување, предметот ќе се движи во права линија, според Њутн законите на движење.
Рамномерно кружно движењо[уреди | уреди извор]
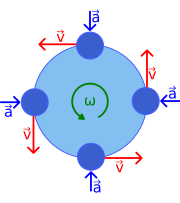

Во физиката, рамномерното кружно движењо опишува движење на телото кое поминува по некој кружен пат со постојана брзина. Бидејќи телото се одликува со кружни движења, неговoто растојание од оската на вртење останува константна во сите времиња. Иако телото е со константна брзина, неговата брзина не е константна: брзина, вектор количина, зависи и од брзината на телото и насоката на движење. Оваа промена на брзината, укажува на присуство на забрзување; ова центрипетално забрзување е со постојана големина и во насока кон оската на вртење. Ова забрзување е, пак, произведено од страна на центрипетална сила која е исто така постојана и насочени кон оската на вртење.
Во случај на ротација околу фиксна оска на цврсто тело што не е многу мало во однос со полупречник на патот, секоја честица од телото опишува константно кружно движење со истата аголна брзина, но со брзина и забрзување кои варираат во однос на позицијата на оската.
Формули[уреди | уреди извор]

За движење во кругот на полупречник r, на обемот на кругот е C = 2π р. Ако периодот за една ротација е Т, аголна стапка на ротација, исто така познат како аголна брзина, ω е:
- и единици се rad/s
Брзината на предметот кој патува по кругот е:
Аголот θ во времето t е:
На аголна забрзување, α, на честички е:
Во случај на константно кружно движење, α ќе биде нула.
Забрзување поради промена во насока е:
Центрипеталната и центрифугалната сила исто така, може да се најдат со користење на забрзувањето:
Вектор односи се прикажани на Слика 1. Оската на вртење е прикажано како вектор ω нормално на рамнината на орбитата и со големината ω = dθ / dt. Насока на ω е избрана со користење на правилото на десна рака. Со оваа конвенција за прикажување на ротација, брзината е дадена со вектор нус производ како
кој е вектор нормален и на ω и на r(t), тангенцијален на орбита, и на големината ω r. Исто така, забрзувањето е дадена со
кој е вектор нормален и на ω и на v(t) на големината ω |v| = ω2 r и спротивен на r(t).[1]
Во наједноставен случај брзината, масата и полупречникот се постојани.
Размислете за тело од еден килограм, се движат во круг со полупречник еден метар, со аголна брзина на еден rad/s.
- Брзината е еден метар во секунда.
- На забрзување од еден метар квадратен на секунда, v2/r.
- Тоа е предмет на центрипетална сила на еден килограм по метар квадратен на секунда, што е еден њутн.
- Импулсот на телото е еден kg·m·s−1.
- Моментот на инерција е еден kg·m2.
- Аголен импулс е еден kg·m2·s−1.
- Кинетичката енергија е 1/2 joule.
- Обемот на орбита е 2π (~6.283) метри.
- Периодот на движење е 2π секунди по 2π rad.
- На честота (2π)−1 херци.
Во поларни координати[уреди | уреди извор]
За време на кружно движење на телото се движи на крива која може да биде опишана во поларен координатен систем како фиксен растојание R од центарот на орбита зема како основа, ориентирани во еден агол θ(t) од некја референта насока. Види Слика 4. Поместениот вектор е радијален вектор од основата на локацијата на честичката:
каде е единичнен вектор паралелно со полупречник вектор во времето t и насочен од рамнината. Тоа е погодно да се воведе ортогонален единичен вектор каде и . Тоа е вообичаено да се ориентираат до точка во насока на движење на орбитата.
Брзината е временски дериват на поместувањето:
Бидејќи полупречникот на кругот е константен, радијалната компонента на брзината е нула. Единичниот вектор има време-неменливи големина на единство, така што времето варира неговиот врв секогаш се наоѓа на кругот на единица полупречник, со агол θ исто како и аголот на . Ако честичката ротира со агол dθ за време dt, па и , опишувајќи лак на кружницата со големина dθ. Види кружницата во долниот лев агол на Слика 4. Оттука:
каде насоката на промена мора да биде нормално да (или, со други зборови, заедно затоа што секоја промена во насока на ќе се промени големината на . Знакот е позитивен, затоа што претставува зголемување во dθ на објектот и се преселија во насока на . Оттука брзината станува:
Забрзувањето на телото, исто така може да биде скршен во радијална и тангентна компонента. Забрзувањето е временски дериват од брзината:
Временски дериват на да се најде на ист начин како и за . Повторно, е единица вектор и формира единица круг со агол што е π/2 + θ. Оттука, зголемување на аголот dθ од имплицира траги лак на големината dθ, и како е ортогонална на имаме:
каде негативен знак е потребно да се задржи е ортогонална на . (Инаку, на аголот помеѓу и ќе се намали со зголемување на dθ.) Види ја кружницата во долниот лев агол на Слика 4. Како резултат на тоа, забрзувањето е:
Центрипеталното забрзување е радијалната компонента, која е насочена радијално навнатре:
while the tangential component changes the magnitude of the velocity:
додека тангентнатаl компонента ја промени големината на брзината:
Користење на комплексни броеви[уреди | уреди извор]
Кружно движење може да се опише со користење на комплексни броеви. Нека x оската е реалната оска и оска биде имагинарна оска. Положбата на телото, тогаш може да се даде како , комплекс "вектор":
каде i е имагинарна единица, и е аргументот на комплексен број, како функција на време, t.
Бидејќи полупречникот е константен:
каде dot покажува диференцијација во однос на времето.
Со оваа нотација брзината станува:
и забрзување станува:
Првиот термин е спротивна на насоката на векторот на поместување, а вториот е нормален, исто како и претходните резултати покажани претходно.
Брзина[уреди | уреди извор]
Слика 1 илустрира вектори на брзина и забрзување за рамномерно движење во четири различни точки во орбитата. Бидејќи брзината v е тангента на кружна патека, на две точки на брзина во иста насока. Иако објектот има константна брзина, неговата насока е секогаш се менува. Оваа промена во брзината е предизвикана од забрзувањето а, чија големина е (како што е на брзината) непроменета, но чија насока постојано се менува. Точките на забрзување се насочени кон внатре (центрипетално) и се нормални со брзината. Ова забрзување е познато како центрипетално забрзување.
За патот со полупречник r, кога агол θ е кон надвор, на растојание кое е кон периферијата на орбита е s = rθ. Затоа, брзина на патување околу орбитата е
- ,
каде аголна стапка на ротација е ω. (Од страна на изменување, ω = v/р.) На тој начин, v е константен, и брзината на вектор v , исто така ротира со постојана големина v, исто го пресметуваме и ω.
Променливи кружни движења[уреди | уреди извор]
Во овој случај на вектор со три забрзувања е нормален на вектор со три брзини,
и на квадратот на соодветните забрзувања, изразена како скаларни непроменливи, исти во сите референтни рамки,
станува израз за кружни движења,
или, преземање на позитивен квадратен корен и со помош на три-забрзувања, го пресметуваме соодветното забрзување за кружно движење:
Забрзување[уреди | уреди извор]
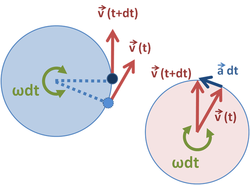
Левата круг на Слика 2 е орбитата која ги покажува брзинските вектори во две соседни времиња. На десната страна, овие две брзини се поместуваат, па нивните опашки се совпаѓаат. Бидејќи брзината е константна, векторите на брзината на десната страна го движат кругот додека времето напредува. За агол на растојание dθ = ωdt промената на v е вектор под прав агол на v и на величина v dθ, што пак значи дека големината на забрзување е дадена со
|v| r
|
1 м/с 3.6 км/ч |
2 м/с 7.2 км/ч |
5 м/с 18 км/ч |
10 м/с 36 км/ч |
20 м/с 72 км/ч |
50 м/с 180 км/ч |
100 м/с 360 км/ч | |
|---|---|---|---|---|---|---|---|---|
| Slow walk | Bicycle | City car | Aerobatics | |||||
| 10 cm 3.9 in |
Laboratory centrifuge |
10 м/с2 1.0 g |
40 м/с2 4.1 g |
250 м/с2 25 g |
1.0 км/s2 100 g |
4.0 км/s2 410 g |
25 км/s2 2500 g |
100 км/s2 10000 g |
| 20 cm 7.9 in |
5.0 м/с² 0.51 g |
20 м/с² 2.0 g |
130 м/с² 13 g |
500 м/с² 51 g |
2.0 км/s² 200 g |
13 км/s² 1300 g |
50 км/s² 5100 g | |
| 50 cm 1.6 ft |
2.0 м/с² 0.20 g |
8.0 м/с² 0.82 g |
50 м/с² 5.1 g |
200 м/с² 20 g |
800 м/с² 82 g |
5.0 км/s² 510 g |
20 км/s² 2000 g | |
| 1 m 3.3 ft |
Playground carousel |
1.0 м/с² 0.10 g |
4.0 м/с² 0.41 g |
25 м/с² 2.5 g |
100 м/с² 10 g |
400 м/с² 41 g |
2.5 км/s² 250 g |
10 км/s² 1000 g |
| 2 m 6.6 ft |
500 мм/с² 0.051 g |
2.0 м/с² 0.20 g |
13 м/с² 1.3 g |
50 м/с² 5.1 g |
200 м/с² 20 g |
1.3 км/s² 130 g |
5.0 км/s² 510 g | |
| 5 m 16 ft |
200 мм/с² 0.020 g |
800 мм/с² 0.082 g |
5.0 м/с² 0.51 g |
20 м/с² 2.0 g |
80 м/с² 8.2 g |
500 м/с² 51 g |
2.0 км/s² 200 g | |
| 10 m 33 ft |
Roller-coaster vertical loop |
100 мм/с² 0.010 g |
400 mм/с² 0.041 g |
2.5 м/с² 0.25 g |
10 м/с² 1.0 g |
40 м/с² 4.1 g |
250 м/с² 25 g |
1.0 км/s² 100 g |
| 20 m 66 ft |
50 мм/с² 0.0051 g |
200 мм/с² 0.020 g |
1.3 м/с² 0.13 g |
5.0 м/с² 0.51 g |
20 м/с² 2 g |
130 м/с² 13 g |
500 м/с² 51 g | |
| 50 m 160 ft |
20 мм/с² 0.0020 g |
80 мм/с² 0.0082 g |
500 мм/с² 0.051 g |
2.0 м/с² 0.20 g |
8.0 м/с² 0.82 g |
50 м/с² 5.1 g |
200 м/с² 20 g | |
| 100 m 330 ft |
Freeway on-ramp |
10 мм/с² 0.0010 g |
40 мм/с² 0.0041 g |
250 мм/с² 0.025 g |
1.0 м/с² 0.10 g |
4.0 м/с² 0.41 g |
25 м/с² 2.5 g |
100 м/с² 10 g |
| 200 m 660 ft |
5.0 мм/с² 0.00051 g |
20 мм/с² 0.0020 g |
130 м/с² 0.013 g |
500 мм/с² 0.051 g |
2.0 м/с² 0.20 g |
13 м/с² 1.3 g |
50 м/с² 5.1 g | |
| 500 m 1600 ft |
2.0 мм/с² 0.00020 g |
8.0 мм/с² 0.00082 g |
50 мм/с² 0.0051 g |
200 мм/с² 0.020 g |
800 mм/с² 0.082 g |
5.0 м/с² 0.51 g |
20 м/с² 2.0 g | |
| 1 км | Голембрзинска железница |
1.0 мм/с² 0.00010 g |
4.0 мм/с² 0.00041 g |
25 мм/с² 0.0025 g |
100 мм/с² 0.010 g |
400 мм/с² 0.041 g |
2.5 м/с² 0.25 g |
10 м/с² 1.0 g |
Нерамномерно[уреди | уреди извор]

Во нерамномерни кружни движења кога објект се движи во кружна патека со различна брзина. Бидејќи брзината е променлива, постои тангенцијало забрзување во прилог на нормално забрзување.
Во нерамномерно кружно движење на нето забрзување (а) е заедно со насока на Δv кој е насочен, внатре во круг но не помине низ неговиот центар (види слика). Нето забрзување може да се реши во две компоненти: тангенцијално забрзување и нормалното забрзување исто така познат како центрипетално или радијално забрзување. За разлика од тангенцијалното забрзување, центрипеталното забрзување е присутен во двете рамномерно и нерамномерно кружно движење.
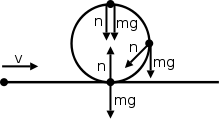
Во нерамномерно кружно движење, нормалната сила не секогаш покажува во спротивна насока на тежината. Пример за тоа е кога некое тело се движи по права патека и излезе од патеката и повторно се врати на неа.
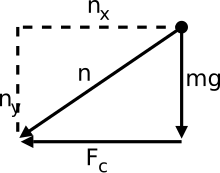
Овој дијаграм ја прикажува нормалната сила што покажува во други насоки, наместо спротивна на силата на тежина. Нормалната сила всушност е збирот на радијалните и тангенционалните сили. Компонентата на силата на тежината е одговорна за тангенционалната сила тука (Ја занемаривме фрикциона сила). Радијалната сила (центрипетална сила) се должи на промената во насоката на брзината како што беше дискутирано претходно.
Во нерамномерно кружно движење, нормалната сила и тежина може да се насочени во иста насока. Двете сили може да се насочени надолу, но објектот ќе остане во кружна патека без да паѓа надолу. Прво, ајде да видиме зошто нормална сила може да биде насочена надолу. Во првиот дијаграм, да речеме дека објектот е човек што седи во авион, двете сили укажуваат само кога ќе стигнат до врвот на кругот. Причината за ова е дека нормалната сила е збирот на тангенционалната сила и центрипеталната сила. Тангентната сила е нула на врвот ((како што не се врши работа кога движењето е нормално на правецот на применетата сила. Овде тежинската сила е нормална на правецот на движење на предметот на врвот на кругот) и центрипеталната сила е насочена надолу, со тоа и нормална сила ќебиде насочена надолу. Од логичка гледна точка, еден човек кој е на патување во авионот ќе биде наопаку на врвот на кругот. Во тој момент, седиштето на личноста е всушност притискање на лицето, што е нормална сила.
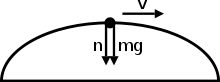
Причината зошто предметот не паѓа кога е подложен на само надолни сили е едноставен. Размислете за тоа што го задржува предметот откако ќе биде фрлен. Откако предметот ќе биде фрлен во воздухот, има само сила на гравитација на Земјата што дејствува на предметот. Тоа не значи дека откако некој објект е фрлена во воздух, тој ќе падне веднаш. Она што го чува тој објект нагоре во воздухот е неговата брзина. Првиот Њутн закон на движење се наведува дека предметот во движење го чува инерцијата, и предметот во воздухот има брзина, тој ќе има тенденција да се задржи да се движи во таа насока.
Променлива аголна брзина за објект што се движи по кружна патека исто така може да се постигне ако вртечкото тело нема хомогена дистрибуција на маса. За нехомогени предмети, неопходно е да се пријде на проблемот како и во.[2]
Апликации[уреди | уреди извор]
Решавање на апликации кои се занимаваат со нерамномерно кружно движење вклучува анализа на сила. Со рамномерно кружно движење, единствената сила која дејствува врз предмет што патува во круг е центрипеталната сила.Во нерамномерни кружни движења, постојат дополнителни сили кои дејствуваат на предметот поради не-нулта тангенцијално забрзување. Иако постојат дополнителни сили кои дејствуваат врз предметот, збирот на сите сили кои дејствуваат на објектот ќе треба да се еднакви на центрипеталната сила.
Радијално забрзување се користи при пресметување на вкупната сила. Тангенцијалното забрзување не се користи при пресметувањето на вкупната сила, бидејќи тоа не е одговорно за одржување на предметот по кружна патека. Само забрзување одговорен за одржување на предметот да се движи во круг е радијалното забрзување. Бидејќи збирот на сите сили е центрипеталната сила, цртањето на центрипеталната сила во слободниот дијаграм на телото не е неопходно и обично не се препорачува.
Користејќи можеме да нацртаме слободни дијаграми на телата за да ги наведеме сите сили кои дејствуваат на секој предмет, а потоа да се нацрта . Потоа, може да се реши сето она што е непознато (тоа може да биде маса, брзина, полупречник на кривина, коефициент на триење, нормално сила, итн.). На пример, визуелниот цртеж погоре покажува предмет на врвот на полукругот кој би бил изразен како .
Во рамномерно кружно движење, вкупно забрзување на предметна кружна патека е еднаков на радијално забрзување. Поради присуството на тангенцијалното забрзување во нерамномерно кружно движење, што повеќе не важи. За да се пронајде вкупното забрзување на предмет во нерамномерно кружно, се бара векторски збир на тангенцијалното забрзување и радијалното забрзување.
Радијалното забрзување уште е еднакво на . Тангенцијалното забрзување е едноставно извод од брзината во која било дадена точка: . Овој корен кој е збир од квадратите на радијалните и тангенцијалните забрзувања е само валиден за кружни движења; за општи движење во рамнина со поларните координати , на Кориолисовите изрази треба да се додаде , додека радијална забрзување тогаш стануваат .
Поврзано[уреди | уреди извор]
- Аголен импулс
- Равенки на движење за кружни движења
- Пример: кружни движења
- Фиктивна сила
- Геостационарна орбита
- Геосинхрона орбита
- Нишало (математика)
- Реактивна центрифугална сила
- Повратно движење
- Едноставно хармонично движење#Еднообразно кружно движење
- Прашка (оружје)
Наводи[уреди | уреди извор]
- ↑ Knudsen, Jens M.; Hjorth, Poul G. (2000). Elements of Newtonian mechanics: including nonlinear dynamics (3. изд.). Springer. стр. 96. ISBN 3-540-67652-X.
- ↑ Gomez, R W; Hernandez-Gomez, J J; Marquina, V (25 July 2012). „A jumping cylinder on an inclined plane“. Eur. J. Phys. IOP. 33 (5): 1359–1365. arXiv:1204.0600. Bibcode:2012EJPh...33.1359G. doi:10.1088/0143-0807/33/5/1359. Посетено на 25 April 2016.
Надворешни врски[уреди | уреди извор]
- Physclips: Механика со анимации и видео клипови од Универзитетот на Нов Јужен Велс
- Кружни Движења Архивирано на 14 декември 2010 г. – поглавје од онлајн учебник
- Кружни Движења Предавање – видео предавање на СМ
- – онлајн учебник со различни анализи за кружно движење




















![{\displaystyle z=x+iy=R(\cos[\theta (t)]+i\sin[\theta (t)])=Re^{i\theta (t)}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3cbaef6788e3f24ac5b98adafca739e98a20613)

![{\displaystyle v={\dot {z}}={\frac {d\left(Re^{i\theta [t]}\right)}{dt}}=R{\frac {d\left(e^{i\theta [t]}\right)}{dt}}=Re^{i\theta (t)}{\frac {d(i\theta [t])}{dt}}=iR{\dot {\theta }}(t)e^{i\theta (t)}=i\omega Re^{i\theta (t)}=i\omega z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/067366fb69351cc859c0f4566c92852b5b55a01c)









