Временско издолжување
Временско издолжување или временско забавување (временско издолжување) — разлика од изминатото време меѓу два настани како што се измерени од набљудувачите кои или се движат релативно еден кон друг или пак се со различни местоположби во однос на гравитациска маса или маси.
Прецизен часовник во мирување во однос на еден набљудувач може да отчукува различно во однос на часовникот на вториот набљудувач. Овој ефект не произлегува од техничките аспекти на часовниците ниту пак од фактот дека на сигналите име потребно време за да се движат, туку зависат од природата на самиот време-простор.
Преглед[уреди | уреди извор]
Часовниците на шатл работат побавно од референтните часовници на Земјата, додека часовниците на ГПС и Галилео сателитите работат побрзо.[1] Ваквата временско издолжување е веќе неколкупати демонстрирана (видиекспериментална потврда подолу), на пример од мали разлики кај атомските часовници на Земјата и во Вселената, иако и двата часовници работат совршено (не се работи за механички дефект). Законите на природата се такви што самото време (i.e. време-простор) ќе се свитка поради разлики во гравитација или брзина – и двете влијаат различно врз времето.[2][3]
Теоретски, а и за да се направи појасен пример, временското издолжување може да влијае брз планирани состаници на астронаутите со напредна технологија и поголеми патувачки брзини. Астронаутите би морале да ги наместат своите часовници да бројат точно 80 години, додека контролната станица - назад на Земјата - би требала да брои 81 година. Астронаутите би се вратиле на Земјата, по нивната мисија, остарени една година помалку од луѓето на Земјата. Покрај тоа, чувството за времето што проаѓа не се менува за никој. Со други зборови, астронаутите на вселенскиот брод, како и екипажот од контролната станица, се чувствуваат нормално, покрај ефектите од временското издолжување (i.e. за тие што патуваат, другите живеат побрзо; додека за тие кои биле во мирување, другите живееле побавно во било кој даден момент).
Бидејќи технологијата ги ограничува брзините на астронаутите, овие разлики се мноуг мали: после 6 месеци на Меѓународната Вселенска Станица (МВС), астронаутскиот екипаж навистина остарел помалку од тие на Земјата, но само за околу 0.005 секунди (ни близу до едната година од теоретскиот пример). Ефектите би биле поголеми доколку астронаутите патуваа поблиску до брзината на светилината (299,792,458 m/s), наместо со нивната вистинска брзина - која е еднаква на брзината на орбитирачкиот МВС , речиси 7,700 m/s.[4]
временското издолжување е предизвикана од разлика во гравитација или пак релативна брзина. Во случајот на МБС, времето е побавно поради брзината во кружната орбитала; овој ефект се намалува од спротивниот ефект на помал гравитациски потенцијал.
Временско издолжување кај релативна брзина[уреди | уреди извор]
Кога двајца набљудувачи се во релативно движење без влијание од никаква гравитациска маса, од нивна гледна точка (движечкиот) часовник на другиот отчукува побавно отколку локалниот часовник. Колку е поголема релативната брзина, толку е поголема и величината на временското издолжување. Овој случај е понекогаш нарекуванспецијално релативна временско издолжување.
На пример, две ракети (A и B) забрзувајќи една после друга во вселената би искусиле временско издолжување. Ако тие некако би имале чист поглед во другата ракета, секој од нив би го гледал часовникот на другиот како се движи побавно. Тоа е, во референтната рамка на ракетата A, сè се движи нормално, но сето останато на ракетата В изгледа дека се движи побавно (и обратно).
Од локална перспектива, времето регистрирано од часовници во мирување спрема локалната референтна рамка (и далеку од гравитациска маса) секогаш изгледа дека поминува со иста брзина. Со други зборови, ако нова ракета, ракетата С, патува паралелно со ракетата А, таа е во "мирување" во однос на ракетата А. Од аспектот на ракетата А, времето на ракетата С би изгледало нормално исто така.[5]
Произлегува едно прашање: доколку ракетата А и ракетата В мислат дека меѓусебното време минува побавно, кој би остарел повеќе доколку би се одлучиле да се сретнат? Со пософистицирано разбирање на временското издолжување кај релативното забрзување, налукувајќи на двоен парадокс излегува дека не е воопшто никаков парадокс (резолуцијата на парадоксот вклучува скок во време, како резултат на вртењето на забрзаниот набљудувач). Слично на ова, разбирањето на двојниот парадокс би помогнало да се објасни зошто астронаутите на МВС стареат побавно (пр. 0.007 секунди побавно за секои шест месеци) иако се под влијание на временско издолжување кај релативното забрзување.
Гравитациска временско издолжување[уреди | уреди извор]

Гравитациската временско издолжување исто така ги вклучува астронаутите од МВС, но има спротивен ефект од временското издолжување при релативна брзина. Едноставно кажано, релативната брзина и гравитацијата го забавуваат времето како што се зголемуваат. Зголемената брзина го забавува времето за астронаутите, додека намалената гравитација го забрзува (астронаутите се изложени на помала гравитација од Земјата). Астронаутите од МВС завршуваат со забавено време бидејќи двата спротивставени ефекти не се еднакво силни. Временското издолжување кај релативна брзина (објаснета погоре) прави поголема разлика и го забавува времето. Време-забрзувачките ефекти на слаба гравитација не би ги поништила ефектите на време-забавувачката брзина освен ако МВС орбитираше многу подалеку од Земјата.
Клучот е во тоа што и двата набљудувачи се различно дистанцирани од значајна гравитациска маса. Генералната теорија на релативност објаснува како за двата набљудувачи часовникот кој е поблизу до гравитациската маса, или подлабоко во нејзиниот "гравитациски бунар", се причинува дека работи побавно од оној кој е подалекуи од масата. Овој ефект не важи само за астронаути во вселената; времето на еден планинар минува малку побргу додека е на врвот на една планина (многу високо и далеку од центарот на гравитација на Земјата) во однос на оние кои се на морско ниво. Како и со секое издолжување, локалното чувство за време е нормално (никој не приметува разлика во сопствената референтна рамка). Во случајот на брзинската временско издолжување, двата набљудувачи ја воочуваа разликата (реципрочен ефект). Сега, со гравитациската временско издолжување, двата набљудувачи, оние кои се на морско ниво и планинарот кој е на врвот на планина, се сложуваат дека часовникот поблиску до гравитациската маса е побавен, како и соодносот на разликата (што значи дека ова издолжување нема реципрочен ефект).
Временско издолжување: специјалната против општата теорија на релативноста[уреди | уреди извор]
Кај теоријата на релативноста на Алберт Ајнштајн, временското издолжување во двете околности може да биде сумирана:
- Во специјалната релативност (или далеку од каква било гравитациска маса),часовниците кои се движат во однос на инерцијалниот систем работат побавно. Овој ефект е опишан прецизно во Лоренцовите трансформации.
- Во општата релативност, часовнитице позиционирани на места со помал гравитациски потенцијал работат побавно. Статиите за гравитациското издолжување на времето и гравитациското црвено поместување даваат подетални информации.
Овие теории може да се комбинираат (како кај астронаутите од МВС).
Преглед на формули[уреди | уреди извор]
Временско издолжување по релативната брзина[уреди | уреди извор]

Формулата за одредување на временското издолжување во специјалната релативност е:
Каде Δt е временски интервал помеѓу два соседни настани (т.е. два настани кои се случуваат на истото место) за точката А во некоја инерцијална рамка (пр. стрелките на часовникот), познати како точно време, Δt′ е временскиот интервал помеѓу тие два исти настани, мерено по некоја друга точка В која инерцијално се движи со брзина v во размер на претходната точка., е релативната брзина помеѓу точката А и часовникот, c е брзина на светлината, и Лоренцовиот фактор (означена со грчката буква гама or γ) е
Thus the duration of the clock cycle of a moving clock is found to be increased: it is measured to be "running slow". Така што, времетраењето на циклусот на часовникот постојано се зголемува, измерено е дека се движи бавно. Опсегот на вакви варијанти во вистинскиот живот, каде v ≪ c, even considering space travel, are not great enough to produce easily detectableи притоа земајќи ги предвид и всленските патувања, не се доволни за да произведат ефекти за лесно приметлива временско издолжување и вакви исклучително мали ефекти може со сигурност да се игнорираат за многу потреби. Само кога објектот ќе се приближи 30,000 км/s (1/10 од брзината на светлината) така што временското издолжување станува важна.
временското издолжување по Лоренцовата константа била предвидена од Јозеф Лармор (1897), барем за електроните што орбитираат во јадрото. Така што “... поединечните електрони ги опишуваат соодветните делови на нивните орбити за неколкупати пократки од [останатиот дел] од системот во односот: math>\scriptstyle \sqrt{1 - \frac{v^2}{c^2}}</math>" (Larmor 1897).временското издолжување на величината која одговара со оваа (Лоренцова) константа е потврдена и преку експерименти,коишто се опишани подолу.
Временско издолжување поради истовремено движење и гравитација[уреди | уреди извор]

Следење на време со голема точност, следењето на сателитите во нискоземската орбита, и одредувањето на времето помеѓу пулсирањето се акции коишто го побаруваат да се земе во обзир комбинираниот ефект на масата и движењето во создавањето на временското издолжување. Практични примери го вклучуваат интернационалното атомско време и неговата релација со барицентричниот стандарден систем којшто се користи за меѓупланетарни објекти.
Ефектите на релативистичката временско издолжување за сончевиот Систем и за земјата можат да бидат моделирани многу прецизно со решението на Шварцчајлд на Ајнштајновите основни равенки. Во Шварцчајлдовиот метрички систем интервалот dtE е пресметан со[7][8]
каде:
- dtE е мал инкремент на точното времеtE (интервал којшто може да биде виден на атомски часовник);
- dtc е мал инкремент во координатите tc(координатно време);
- dx, dy и dz се мали инкременти на трите координати x,y,z на позициите на часовникот; и
- GM i/r i ја претставува сумата на Њутновите гравитациски потенцијали коишто се случуваат поради масите во соседството, засновани на нивните растојанија r i од часовникот. Оваа сума GM i/r i вклучува секакви бранови потенцијали, и е претставена како U (користејќи ја астрономската конвенција за знаци). Координатното забрзување на часовникот е одредена со
Координатното време tc е времето кое што би било прочитано од хипотетичкиот “ координатен часовник“ којшто се наоѓа бесконечно далеку од сите гравитациски маси ( U=0), и стационарно во координатниот систем ( V=0). Точната релација помеѓу бројот на интервалите на точното време и бројот на интервалите на координатното време за часовник со радијална компонента од забрзување е : Каде: v|| е радијално забрзување, и U = GM i/r i е Њутновиот потенцијал,еднаков на половина од забрзувањето потребно за телото да излезе од гравитацијата на вселенското тело на квадрат. Горенаведената равенка е точна по претпоставките на Шварцчајлдовото решение.
Експериментална потврда[уреди | уреди извор]
Временското издолжување било испробано голем број на пати. Рутинската работа која што се правела постојано во забрзувачи на честички уште од 1950-тите, како што е CERN, која што континуирано извршува тестови на временското издолжување на специјалниот релативитет. Специфични експерименти вклучуваат:
Тестирање на вренските издолжувања на забрзувањето[уреди | уреди извор]
- Ивес и Стивел (1938, 1941). Изразената цел на овие експерименти била да се потврди ефектот на времеското издолжување, која што била предвидена од Лармор-Лоренцовата теорија за етерот, коишто се случуваат со движење низ етерот користејќи го Ајнштајновиот предлог дека Доплеровиот ефект во канални зраци би бил соодветен експеримент. Овие екперименти го пресметале Доплеровото менување на зрачењето која што е емитирана од катодни зраци,кога се гледа директно од напред и директно од позади. Високите и ниските честоти не биле класично предвидените вредности
- Високите и ниските честоти на зрачењето на подвижните објекти биле пресметани како[9]
- Како што бил заклучокот на Ајнштајн (1905) од Лоренцовата трансформација , кога објектот се движи споро со Лоренцовата константа.
- Роси и Хал (1941) ја пспоредиле застапеноста на муоните создадени од космичките зраци на врвот на една планина во споредба со тие коишто биле набљудувани на морско ниво. Иако времето кое што им требало на муоните да пристигнат од врвот на планината до базата се неколку пола животи на муон, муонскиот примерок бил само малку намален. Ова е објаснето со временското издолжување која што е блиску поврзана со големата брзина на експериментите. Со што се заклучило, дека муоните се распаѓале околу 10 пати поспоро во споредба со тоа кога тие би биле во мирување во експериментите.
- Хаселкамп, Мондри и Шарман [10] (1979) го измериле Доплеровото менување од извор којшто се движи по прави агли до границите на видливоста ( инверзното Доплерово менување). Најопштата врска помеѓу честотите на зрачењето од движечките извори е пресметана со:
- како што заклучил Ајнштајн (1905).[11] За ϕ = 90° (cosϕ = 0) ова се намалува до fdetected = frestγ. Така што нема изнверзно Доплерово менување, и ниската честота на изворот којшто се движи може да биде приврзана само на ефектот на времеското издолжување.
- Во 2010 временското издолжување била набљудувана при брзини помали од 10 метри во секунда користејќи оптички атомски часовници поврзани со 75 метри оптичко влакно.[12]
Тестови на гравитациско временско издолжување[уреди | уреди извор]
- Во 1959 Роберт Паунд and Глен А. Ребка го измериле малото црвено гравитациско менување во честотата на светлина емитирана на ниска висина, каде Земјиното гравитациско поле е релативно поинтензивно. Резултатите биле во 10% од предвидувањата на општиот релативитет. Во 1964, Паунд и Џ.Л. Шнајдер го измериле резултатот со 1% од вредноста предвидена со гравитациската временско издолжување.[13] (See Pound–Rebka experiment)
- Во 2010 гравитациската временско издолжување била измерена на Земјината површина со висинска разлика од само 1 метар со користење на оптички атомски часовници.[12]
Тестови за комбинираниот ефект помеѓу забрзувањето и гравитациската временско издолжување[уреди | уреди извор]
- Хафел и Китинг, во 1971, летале цезиумски атомски часовници источно и западно околу Земјата на комерцијални летови за да го споредат поминатото време споредено со времето на часовник којшто останал во Американска морнаричка обзерваторија. Се случиле два различни ефекти. Часовницците биле изложени на стареење побрзо ( покажувале повеќе поминато време) од референтниот часовник, бидејќи тие биле повисоко (на послаб) гравитациски потенцијал за поголем дел од траењето на патувањето. Но , исто така во контраст, часовниците кои се движеле се очекувало да застарат многу поспоро од причина дека се движеле со поголема брзина. Од Од патеките на секое патување, теоријата предвидела дека часовниците кои летале, споредено со референтните часовници во американската обзерваторија требало да изгубат 40±23 наносекунди за време на патувањето на источната страна и требало да добијат 275±21 наносекунди за време на патувањето на запад. Релативно на големината на атомското време во американската обзерваторија часовниците кои летале изгубиле 59±10 наносекунди за време на патувањето на исток и добиле 273±7 наносекунди за време на патувањето на запад (каде што е претставено стандардното отстапување). Во 2005 Националната лабароторија за физика на Велика Британија ја пријавиле нивната лимитирана репликација на овој експримент. Експриментот на В. Британија се разликувал од оригиналниот по тоа што часовниците со цезиум биле пратени на пократок пат ( Лондон- Вашингтон, и обратно), но часовниците биле попрецизни. Добиените резултати се во 4% од предвидувањето на релативитетот со несигурноста на мерењата.[14] In 2005, the National Physical Laboratory in the United Kingdom reported their limited replication of this experiment.[15]
- Глобалниот Систем за Позиционирање може да биде сметан за експримент којшто континурано работи на специјалниот и генералниот релативитет. Часовниците во орбитата се корегирани и за специјалната и општата релативитистичка временско издолжување како што е опишано погоре, за да (како што е набљудувано од Земјината површина) би работеле со ист интервал како часовниците на површината на Земјата.[16]
Животниот век на муонот[уреди | уреди извор]
Споредбата на животните векови на муоните со различни брзини е можна. Во лабораторија се произведуваат спори муони, и во атмосферата многу брзи муони се добиваат од космичките зраци. Земајќи го животниот век на муоните во мирување како лабораториска вредност од 2,197 μs, животниот век на муон произведен од космички зрак којшто патува со брзина од 98% од брзината на светлината е околу 5 пати подолг во корелација со набљудувањето.[17] Во прстенот за чување на муони во CERN животниот век на муоните којшто се движи околу γ = 29.327 бил најден дека е променет на 64.378 μs, со која што се потврдува временското издолжување на точноста од 0.9 ± 0.4 делови на 1000. Во овој експеримент “ часовникот” е времето потребно за да се распадне муон, и процесите се случуваат во движечкиот муон по негов негов “ времеснки интервал” којшто е многу поспор од лабораторискиот часовник.
Вселенски летови[уреди | уреди извор]
временското издолжување ќе направи да биде можно патниците на брзодвижечки возила да патуваат во иднината додека би старееле многу малку, со тоа дека големата брзина би го успорувала траењето на времето на возилото релативно со тоа на некој набљудувач. Според тоа, часовникот на леталото( и според релативитетот, секој човек којшто патува со него) покажува помалку поминато време од часовниците на набљудувачите на Земјата. За навистина поголеми брзини ефектот е драматичен. На пример, една година од патување кореспондира со десет години на Земјата. Всушност, константно 1 g забрзување би дозволило луѓето да патуваат низ целиот познат универзум во еден човечки животен век.[18] The space travelers could return to Earth billions of years in the future. A scenario based on this idea was presented in the novel Planet of the Apes by Pierre Boulle.
Многу пореално користење на овој ефект би било да овозможи на луѓето да патуваат до блиски ѕвезди без да го потрошат целиот живот на летало. Но, каква било употреба на временско издолжување за време на интерстерално патување би барало користење на нова напредна метода за погон. Проектот Орион е голем обид за остварување на оваа идеја. Денешната технологија за вселенски летови има фундаментални теоретски лимити коишто се засноваат на практичен проблем дека зголемена вредност на енергија е потребна за погон кога леталото ќе се доближи до брзината на светлината. Веројатноста на судирање со мал вселенски отпад и други материјали е исто така практична лимитација. Со забрзувањата како и да е временското издолжување се случува, но е премногу мала да биде фактор во вселенското патување. Патувањето во региони во вселенатѕа каде гравитациската временско издолжување се случува како во гравитациското поле на црната дупка, но надвор од границите на евент хоризонтот (границите на црната дупка од каде светлината не излегува) , исто така може да донесе резултати коишто се точни според теоријата.
Временско издолжување при константна сила[уреди | уреди извор]
Во специјален релативитет, временското издолжување е едноставно опишана како околностете каде релативното забрзување е непроменливо. Без разлика , Лоренцовите равенки дозволуваат да се измери точното време и движењето во Вселената во едноставен случај на вселенско летало кое што е применет со сила за време на масата на единица мерка, релативно на референтен објект во константно забрзување, еднакво на g низ периодот на пресметување.
Нека t е времето во рамки коишто се наречени мирувачки рамки. Нека x е просторна координата, и да дозволува насоката на константнотоо забрзување како и брзината на вселенскиот брод ( релативно на мирувачката рамка) е паралелна на x-оската. Да претпоставиме дека позицијат на вселенското летало во време t=0 кое ќе ни биде x=0 и забрзувањето да биде v0 и дефинирајќи го следниот израз
Формулите коишто следат опишуваат:[19]
Позиција:
Брзина:
Точното време:
Во случајот каде v(0) = v0 = 0 и τ(0) = τ0 = 0 интегралот може да биде изразен како логаритамска функција, или како инверзна хиперболична функција:
Геометрија на вселенското време на временското издолжување на забрзувањето[уреди | уреди извор]

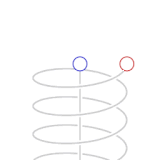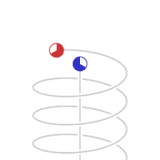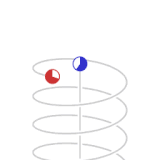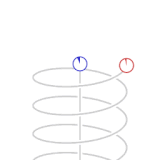
Зелените точки и црвените точки во анимацијата претствауваат вселенски летала. Леталата од зелената флото немаат забрзување релативно едно на друго, па часовниците на поединечни летала исто време поминува релативно едно на друго, и може да наместат процедура за да одржуваат синхронизирано стандардно време на флотата. Бродовите од црвената флота се движат со забрзување од 0.866c земајќи ја во обзир зелената флота.
Сините точки ги претствуваат пулсирањата на светлината. За еден циклус на пулсирање на светлината помеѓу две зелени летала е потребно две секунди од зеленото време, по една секунда за секоја гранка. Како што можеме да видиме од перспективата на црвените, времето за патување на пулсирањата на светлината коишто ги споделуваат помежу себе е една секунда од црвено време на секоја гранка. Видено од перспективата на зелените, циклусот на споделување на светлински пулсирања на црвените летала патува дијагонален пат којшто е долг две светлосни секунди ( како што може да биде набљудувано од перспективата на зелените, црвените патуваат 1,73 ( ) светлосни секунди на растојание за секои две секунди од зелено време.) Еден од црвените бродови емитува светлосен пулс кон зелените секоја секунда од црвенотот време. Овие пулсови се добиваат од леталата на зелената флота во интервали од две секунди мерени во зелено време. Во анимацијата не е покажано дека сите апекти на физиката се пропорционално вклучени. Светлосните пулсеви кои се емитирани од црвените со одредена честота како што би било пресметано во црвено време се примени на помала честота пресметани од детекторите на зелената флота кои мерат според зелено време, и обратно. Анимацијата кружи помеѓу зелената перспектива и црвената перспектива, за да даде значење на симетријата. Бидејќи не постои такво нешто како апсолутно движење во релативитет ( како што е случајот на Њутновите механики) , заедно и зелените и црвените флоти би биле во право да се сметаат себеси неподвижни во нивната рамка за референца. Повторно, од огромно значење е да се разбере дека резултатите од овие односи и пресметки ја рефлектираат реалната состојба на леталата која што произлегува од нивната ситуација на релативно движење. Овоа не е грешка на методот на пресметка или комуникација.
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ 1,0 1,1 Ashby, Neil (2003). „Relativity in the Global Positioning System“ (PDF). Living Reviews in Relativity. 6: 16. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. Архивирано од изворникот (PDF) на 2015-11-05. Посетено на 2015-12-24.
- ↑ Toothman, Jessika. „How Do Humans age in space?“. HowStuffWorks. Посетено на 2012-04-24.
- ↑ Lu, Ed. „Expedition 7 – Relativity“. Ed's Musing from Space. NASA. Архивирано од изворникот на 2016-01-19. Посетено на 2012-04-24.
- ↑ Lu, Ed. „Expedition 7 – Relativity“. Ed's Musing from Space. NASA. Архивирано од изворникот на 2016-01-19. Посетено на 2015-01-20. Всушност 0.007 секунди се спомнува како точен резултат, но тоа е само груба пресметка.
- ↑ За извори за специјална релативно временско издолжување, погледнете ја експозицијата на Алберт Ајнштајн, публицирана на англиски јазик (1920) како Einstein, Albert (1920). „On the Idea of Time in Physics“. Relativity: The Special and General Theory. Henri Holt. ISBN 1-58734-092-5. и исто така во секциите од 9–12. Погледнете ги и членовите Специјална релативност, Лоренцови трансформации и Релативност на истовременост.
- ↑ Ashby, Neil (2002). „Relativity in the Global Positioning System“. Physics Today. 55 (5): 45. Bibcode:2002PhT....55e..41A. doi:10.1063/1.1485583.[мртва врска]
- ↑ види равенки 2 & 3 (combined here and divided throughout by c2) at pp. 35–36 in Moyer, T. D. (1981). „Transformation from proper time on Earth to coordinate time in solar system barycentric space-time frame of reference“. Celestial Mechanics. 23: 33–56. Bibcode:1981CeMec..23...33M. doi:10.1007/BF01228543.
- ↑ A version of the same relationship can also be seen at equation 2 in Ashbey, Neil (2002). „Relativity and the Global Positioning System“ (PDF). Physics Today. 55 (5): 45. Bibcode:2002PhT....55e..41A. doi:10.1063/1.1485583.
- ↑ Blaszczak, Z. (2007). Laser 2006. Springer. стр. 59. ISBN 3540711139.
- ↑ Hasselkamp, D.; Mondry, E.; Scharmann, A. (1979). „Direct observation of the transversal Doppler-shift“. Zeitschrift für Physik A. 289 (2): 151–155. Bibcode:1979ZPhyA.289..151H. doi:10.1007/BF01435932.
- ↑ Einstein, A. (1905). „On the electrodynamics of moving bodies“. Fourmilab.
- ↑ 12,0 12,1 Chou, C. W.; Hume, D. B.; Rosenband, T.; Wineland, D. J. (2010). „Optical Clocks and Relativity“. Science. 329 (5999): 1630–1633. Bibcode:2010Sci...329.1630C. doi:10.1126/science.1192720. PMID 20929843.
- ↑ Pound, R. V.; Snider J. L. (November 2, 1964). „Effect of Gravity on Nuclear Resonance“. Physical Review Letters. 13 (18): 539–540. Bibcode:1964PhRvL..13..539P. doi:10.1103/PhysRevLett.13.539.
- ↑ Nave, C. R. (22 August 2005). „Hafele and Keating Experiment“. HyperPhysics. Архивирано од изворникот на 2017-04-18. Посетено на 2013-08-05.
- ↑ „Einstein“ (PDF). Metromnia. National Physical Laboratory. 2005. стр. 1–4. Архивирано од изворникот (PDF) на 2008-10-30. Посетено на 2016-03-28.
- ↑ Kaplan, Elliott; Hegarty, Christopher (2005). Understanding GPS: Principles and Applications. Artech House. стр. 306. ISBN 1-58053-895-9. Extract of page 306
- ↑ Stewart, J. V. (2001). Intermediate electromagnetic theory. World Scientific. стр. 705. ISBN 981-02-4470-3.
- ↑ Calder, Nigel (2006). Magic Universe: A grand tour of modern science. Oxford University Press. стр. 378. ISBN 0-19-280669-6.
- ↑ See equations 3, 4, 6 and 9 of Iorio, Lorenzo (2004). „An analytical treatment of the Clock Paradox in the framework of the Special and General Theories of Relativity“. Foundations of Physics Letters. 18: 1–19. arXiv:physics/0405038. Bibcode:2005FoPhL..18....1I. doi:10.1007/s10702-005-2466-8.
Надворешни врски[уреди | уреди извор]
Грешка во наводот: Има ознаки <ref> за група именувана како „Note“, но нема соодветна ознака <references group="Note"/>.













