Питагорова теорема

Во математиката, Питагоровата теорема ја изразува врската што постои помеѓу трите страни на правоаголен триаголник во Евклидовата геометрија. Ако a и b се катетите, а c хипотенузата на правоаголен триаголник, важи еднаквоста:
односно изразено со зборови:
Плоштината на квадратот конструиран над хипотенузата на правоаголен триаголник е еднаква на збирот на плоштините на квадратите конструирани над катетите на тој триаголник.
Теоремата го добила името по старогрчкиот математичар Питагора, за кој традиционално се смета дека ја открил и докажал,[1] иако денес е сигурно дека била позната многу пред Питагора.[2] [3]
Питагоровата теорема е една од најосновните и најважните математички теореми. Препознатливата слика на правоаголен триаголник со конструирани квадрати на сите три страни, користена за визуелна претстава на самото тврдење, послужила како основа за генерирање на фракталот наречен Питагорово дрво.
Историја[уреди | уреди извор]

Историски гледано, откривањето и разбирањето на Питагоровата теорема поминало низ неколку фази:
- алгебарско истражување на постоење на Питагорова тројка,
- подобро разбирање на односот помеѓу страните на правоаголен триаголник, односно односот помеѓу соседните агли на триаголникот, што е последица на стекнување на сè поголеми знаења за рамнините и површините и
- наоѓање голем број на различни докази на теоремата.
Древни цивилизации[уреди | уреди извор]
Врската што постои помеѓу страните на триаголникот чии должини се 3, 4 и 5 им била позната уште на Вавилонците, 2000 г. пр. н. е.[4] а може да се најде и во познатата кинеска книга Девет книги за математичка вештина, која се претпоставува дека е напишана околу 1100 година пр. н. е.[5]
Познатата вавилонска глинена плоча која го носи бројот 322 во Плимптоновата збирка е таблица од Питагорови тројки со 15 реда создадена во 1800 пр. н. е. Старите Египќани знаеле за четири Питагорови тројки, како што е потврдено во папирус датиран за време на владеењето на XII династија, околу 2000 пр. н. е., во која меѓу другото е можно да се најде и односот:
- . [5]
Таа е еквивалентно на Питагоровата тројка (3, 4, 5) ако изразот се прошири за да се ослободи од дропките.
Питагоровите тројки може да се најдат и во Сулвасутрите, светите песни на хиндусите, од 5-4 век пр .н. е., кои кажуваат за начинот на добивање прави агли со помош на јаже со 3-4-5, т.е. 12-16-20, 15-20-25, 5-12-13, 15-36-39, 8-15-17 и 12-35-37 јазли врзани на еднакви растојанија. Користењето јаже за одредување прав агол имало своја практична примена во древно време, на пример парцелизирање на земјиштето, а луѓето што се занимавале со тоа биле наречени затегнувачи на јаже (грчки: Λρπεδονάπται).[6] Сепак, според некои автори, малку е веројатно дека Египќаните всушност користеле јаже со 12 јазли за да одредат прав агол, и нема очигледни докази дека знаеле дека триаголникот со страни (3, 4, 5) е правоаголен.[7]
Питагора[уреди | уреди извор]
Традиционално, откривањето на теоремата му се припишува на Питагора, старогрчки филозоф и научник, кој денес е познат посредно преку подоцнежните извори. Според нив, Питагора е роден околу 570 г. пр. н. е. на островот Самос, веројатно бил ученик на Талес, а дел од својот живот го поминал патувајќи низ Египет и Персија, така што, по враќањето во родниот Самос, наишол на тиранската власт на Поликрат, за што се верува, дека била причина да се пресели во Кротон каде ја основал познатата Питагорејската школа.[8] Питагорејците тврделе дека теоремата ја открил Питагора и дека во знак на благодарност им жртвувал стотина бикови на боговите.[9] Проблемот со прецизното утврдување на правата вистина е последица на тоа што Питагорејците усно го пренесувале стекнатото знаење, кое се сметало за свето и било строго чувано. Покрај тоа, новите откритија често му се припишувале на голем учител, додека вистинскиот пронаоѓач останувал непознат. Ова е поткрепено со фактот дека името на Питагора не се споменува никаде во изјавата за теоремата што се појавува во Евклидовите Елементи.[10] Денес постојат неколку хипотези:
- Питагора ја презел теоремата од Вавилонците, односно бил само посредник помеѓу знаењето што доаѓало од Исток и Грците. Иако, според античките извори, Питагора ги посетил Египет и Вавилон, оваа инобликција не е сигурна.
- Питагора ја формулирал и докажал теоремата за прв пат независно од вавилонските извори. Овој пристап бил широко прифатен во древно време.
- Питагора слушнал за теоремата на неговите патувања, но тој бил првиот што го докажал тоа. Сосема е јасно дека ниту Египќаните ниту Вавилонците не отишле подалеку од секојдневната примена на теоремата за практични цели. На пример, во Каирскиот папирус, откриен во 1938 година, а дешифриран во 1962 година, има 40 математички задачи, од кои девет се решени со помош на Питагоровата теорема. Една од тие задачи гласи:
- „Скала долга 10 лакти е потпрена на ѕид, така што нејзината основа е 6 лакти од работ на ѕидот. Колку високо се протега таа скала?“
- Меѓутоа, иако теоремата се користи во решавањето на проблемот, нема обид да се обопшти, ниту да се докаже.[11]
- Питагора не учествувал во откривањето на теоремата, но првиот доказ го пронашле неговите студенти.[12]
Првото зачувано дело во кое Питагора се поврзува со исказот на теоремата е Плутарховиот Етички зборник - Моралија, напишан на крајот на првиот или почетокот на вториот век од новата ера. Во него се наведуваат стихови од едно незачувано Аполодорово дело од вториот век пр. н. е. Според Плутарх,
кога Питагора го открил тој прочуен став,
заради тоа понудил сјајна жртва волови.
Истите стихови ги наведува Атенеј од Невкратис, во неговото дело Гозба на учените, на почетокот на третиот век од нашата ера.[13]
Следбеници[уреди | уреди извор]
Првиот писмен доказ за Питагоровата теорема се појавува само 150 години подоцна, во првата и шестата книга од Евклидовите Елементи, каде што, според Прокло, доказот од шестата книга е единствениот изворен Евклидов доказ во Елементите, додека доказот од првата книга му се припишува на Евдокс.[10]
Околу 250 пр. н. е. Архимед приближно ја одредува вредноста на бројот Пи користејќи ја Питагоровата теорема и впишани и опишани многуаголници во круг. Во 2 век пр. н. е., Клавдиј Птоломеј ја докажува теоремата во неговиот Алмагест:
- „Производот на дијагоналите на тетивен четириаголник е еднаков на збирот на производите на неговите спротивни страни.“ [14]
Оттука, во посебниот случај кога тетивниот четириаголник е всушност правоаголник, се добива Питагоровата теорема.
Херон од Александрија подоцна[15] ја докажал формулата со која може да се пресмета плоштината на произволен триаголник преку неговите страни користејќи пропорции. Денес, таа формула се докажува со помош на Питагоровата теорема.
Во 3 век од нашата ера Папос докажал проширена верзија на Питагоровата теорема која се применува на произволен триаголник, а шест века подоцна, Ал Харани дал доказ за друго обопштување што се применува на произволен триаголник.
Формулирање на теоремата[уреди | уреди извор]

Според теоремата:
Во кој било правоаголен триаголник, плоштината на квадратот конструиран над хипотенузата (страната спроти правиот агол) е еднаква на збирот на плоштините на квадратите конструирани над катетите (страните што се среќаваат во правиот агол на триаголникот).
Овој исказ обично се наведува во следниов облик:
Квадратот над хипотенузата е еднаков на збирот на квадратите над катетите.
Ако c е должината на хипотенузата, а a и b се должините на преостанатите две страни, теоремата може да се напише користејќи ја следната еднаквост:
или, изразено од таму:
Ако хипотенузата е позната и треба да се одреди една од катетите, можно е да се користи една од следните две еднаквости (кои се добиваат од почетната еднаквост, со решавање на соодветната непозната):
или
Од наведените еднаквости може да се забележи дека односот меѓу страните на правоаголен триаголник е таков што, во случај една од нив да е со непозната должина, може да се определи со помош на преостанатите две познати страни. Обопштувањето на оваа теорема, позната како косинусна теорема, овозможува пресметување на должината на третата страна на произволен триаголник, ако се познати должините на преостанатите две страни и големината на аголот што тие го покриваат, што е една од поставките на задачата наречена решавање на триаголник. Ако познатите страни определат прав агол, косинусната теорема се сведува на Питагоровата теорема.
Неевклидски геометрии[уреди | уреди извор]

Во сферната геометрија, на единичната сфера, за правоаголен сферен триаголник ABC чии должини на страните се соодветно a, b и c, Питагоровата теорема има облик:
Доколку полупречникот на сфера е со должина РРР, еднаквоста станува:
Во хиперболична рамнина претставена со Поенкаревиот модел на диск, ако е правоаголен триаголник со катети и хипотенуза, Питагоровата теорема има облик:
каде хиперболичниот косинус е дефиниран со:
Хилбертови простори[уреди | уреди извор]
Вообичаена норма на реалниот Евклидов простор се воведува со користење на скаларен производ . Векторскиот простор со норма воведена со помош на скаларен производ се нарекува предхилбертов простор. Ако предхилбертовиот простор е комплетен во однос на неговата метрика, тој се нарекува Хилбертов простор. Ова е секогаш случај во конечнодимензионални простори како што е , но бесконечнодимензионалните предхилбертови простори не мора да бидат Хилбертови.
Ако е во реален простор со скаларен производ (предхилбертовиот простор) воведена норма на векторот со:
- ,
со соодветните својства[19], потоа за ортогонални вектори и Питагоровата теорема добива облик:
- . [20]
Докази[уреди | уреди извор]
Со векови, Питагоровата теорема служела како вдахновение за нови математички докази, кои ги пронашле и луѓе кои не биле професионални математичари. Во книгата Питагорово тврдење (англиски: The Pythagorean Proposition) од Елиша Скот Лумис ( англиски: Elisha Scott Loomis), првично објавена во 1927 година, која била дополнета со нови докази во 1940 година, можно е да се најдат сите познати докази до нивното објавување, вкупно 371. Меѓу другото, таму се наведени Питагоровиот и Евклидовиот доказ, потоа најкраткиот и најдолгиот доказ кој му се припишува на Лежандр, па Птоломеевиот, Леонардовиот, Хајгенсовиот и Лајбницовиот, како и доказот на Џејмс Гарфилд, од времето пред да стане претседател на САД.[21]
Питагоров доказ[уреди | уреди извор]
Иако постојат материјални докази дека врската помеѓу катетите и хипотенузата на правоаголен триаголник им била позната на древните цивилизации, она што одлучило дека теоремата го добила името по Питагора е фактот што тој бил првиот што го докажал тоа. Меѓутоа, бидејќи во негово време немало соодветен материјал за запишување, знаењето стекнато од питагорејците било пренесувано усно, а не постои сигурен извор врз основа на кој со сигурност би можело да се тврди како изгледал изворниот Питагоров доказ. Во неговите Елементи, Евклид дал два докази за теоремата, прв во првата книга,[22] доказ целосно заснован на односите на површините, а потоа во шестата книга,[23] доказ кој користи сличност и е многу поедноставен. Со оглед на тоа што геометријата не била доволно развиена во времето на Питагора, малку е веројатно дека тој го користел првиот доказ, а ако го користел вториот, тогаш тој не бил целосен, бидејќи целосната теорија на сразмерност ја дал дури Евдокс, кој живеел два века по Питагора. Од друга страна, многу е веројатно дека Питагора прв ја докажал теоремата во случај на рамнокрак правоаголен триаголник, бидејќи овој доказ бил познат дури и на Хиндусите, а тој можел да го слушне на неговите патувања по Средоземјето. Дали и тој го докажал општиот случај не се знае, но се претпоставува дека го разгледувал. Тој е традиционално заслужен за докажување на општ случај кој веќе бил познат во древна Кина.[21]
Евклидови докази[уреди | уреди извор]
Во своите Елементи, Евклид ја докажува Питагоровата теорема на две места, прво во првата, а потоа во шестата книга. Првиот доказ е доста тежок за следење, и според Прокло, му припаѓа на претходникот на Евклид, Евдокс, како и теоријата на пропорционалност изложена во петтата книга на Елементите.[21] Постојат различни толкувања за тоа зошто Евклид избрал да ја докаже теоремата на потежок начин во првата книга, иако во негово време биле познати поедноставни докази. Од една страна, повеќето од овие докази вклучуваат поделба на правоаголниот триаголник на помали, слични триаголници и користење на својствата на пропорционалност за да се изведе соодветната еднаквост, но тие не се претставени до петтата книга, додека сличноста е опфатена во шестата книга. Од друга страна, бидејќи старите Грци ги толкувале сите аритметички операции преку геометријата, многу е веројатно дека првиот доказ дошол природно кај Евклид - бидејќи тој ја гледал Питагоровата теорема како однос помеѓу површините. Според Прокло, вториот доказ е целосно Евклидов, згора на тоа, тој е единствениот изворен Евклидов доказ во Елементите.[21]

Суштината на првиот доказ е дека, ако со A, B и C се означени темињата на правоаголен триаголник со прав агол кај темето A, и ако од тоа теме се спушти висина на хипотенузата која се продолжува до спротивната страна на квадратот над хипотенузата, таа ќе го подели тој квадрат на два правоаголници, чии плоштини ќе бидат еднакви на плоштините на квадратот над поблиската катета.
За формален доказ, прво е потребно да се покаже дека важат следните елементарни леми:
- (САС став кон складноста на триаголниците) Ако две страни на еден триаголник се еднакви на две страни на друг триаголник, и ако аглите кои ги зафаќаат тие парови со еднакви страни се исто така еднакви, тогаш триаголниците се складни.[24]
- Плоштината на триаголникот е еднаква на половина од плоштината на кој било паралелограм конструиран над двете страни од тој триаголник.[25]
- Плоштината на кој било правоаголник е еднаква на производот на две соседни страни.
- Плоштината на кој било квадрат е еднаква на производот на неговите две страни (тоа следи од претходната лема).
Интуитивната идеја на доказот е дека квадратите над катетите се преобразуваат во паралелограми со иста плоштина, кои потоа со нова преобразба се вклопуваат во правоаголниците на кои е поделен квадратот над хипотенузата.[26]

- Нека е правоаголен триаголник со прав агол на темето.
- На секоја од страните, и се нацртани квадрати, и соодветно.
- Од точка, нормала се спушта на страницата, која е продолжена до пресекот со страницата и е исто така паралелна со i . Нејзините пресеци со страни и соодветно се означени со и .
- Со поврзување на точките i, односно i, се добиваат триаголници i.
- Аглите и се правилни, па точките, и се колинеарни . Сличен заклучок е донесен и за точките и .
- Аглите и се правилни, што значи дека аголот е еднаков на аголот, бидејќи и двата се еднакви на збирот на правиот агол и аголот.
- Бидејќи страната е еднаква на страната и еднаква, триаголникот е складен на триаголникот.
- Бидејќи точките се колинеарни, правоаголникот има двојно поголема површина од триаголникот.
- Бидејќи точките се колинеарни, квадратот има двојно поголема површина од триаголникот.
- Од горенаведеното произлегува дека правоаголникот има иста површина како квадрат, што е еднакво на ².
- Слично на тоа, можно е да се покаже дека правоаголникот мора да има иста површина како квадрат кој е ².
- Додавањето на добиените равенства ќе биде ² + ² =
- Како што е, важи
- Оттука ² + ² = ², бидејќи е квадрат.
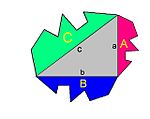
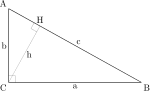
Можно е Евклид да бил свесен за тешкотијата на овој доказ и затоа во шестата книга докажал малку поопшт случај на Питагоровата теорема користејќи сличност. Според ова тврдење, во случај на правоаголен триаголник, геометриската фигура (без ограничувањето дека мора да биде квадрат) конструирана над хипотенузата е еднаква по површина на збирот на плоштините на слични и слично конструирани геометриски фигури. над нозете . [23]
- Нека биде правоаголен триаголник со прав агол на темето.
- Аналогно на претходниот доказ, потребно е да се спушти нормалата од темето на правиот агол до хипотенузата. Основата на нормалата е означена со .
- Бидејќи е нормално на и е нормално на, аглите и се еднакви на аглите со нормални катети.
- Последица е тоа што триаголниците се и слични едни на други и слични на почетниот триаголник, па нивните соодветни страни се пропорционални.
- Од еднаквоста и, со вкрстено множење се добива дека ²= и ²= се валидни.
- Додавањето на добиените равенства ќе биде ²+²=
- Бидејќи, ²+²=² е валиден.
Покрај горенаведените изјави, во првата книга на Елементите, Евклид докажал и изјава во спротивна насока од Питагоровата теорема, според која правоаголен триаголник е единствениот триаголник каде што важи еднаквоста ²+²=². [27]
Гарфилдов доказ[уреди | уреди извор]

Друг особено значаен геометриски доказ, во кој не се користат квадрати над страните, бил откриен околу 1876 година од Џејмс Гарфилд, кој подоцна станал дваесеттиот претседател на САД. Според Илиша Лумис, доказот бил резултат на една од математичките дискусии на Гарфилд со другите членови на Конгресот.[21]
Идејата на доказот е да се додаде уште еден соодветен триаголник на почетниот триаголник, така што пократката катета од првиот и подолгата катета од вториот ќе лежат на права линија и ќе тргнуваат од истото теме. Потоа, со спојување на преостанатите две темиња од триаголниците кои припаѓаат на хипотенузите, се добива правоаголен трапез чии основи се со должина i и висина со должина . Од една страна, неговата плоштина може да се добие како производ од полузбирот на основите и висината, а од друга страна, како збир на плоштините на трите триаголници на кои е поделен, така што:
Леонардов доказ[уреди | уреди извор]


Следниот доказ му се припишува на познатиот италијански уметник и научник Леонардо да Винчи,[28] и се потпира на симетријата и ротацијата.[29]
- Нека ABC е правоаголен триаголник со прав агол кај темето C.
- Над секоја од страните CA, BC и AB конструирани се квадрати, ACED, BCFG и ABHJ соодветно.
- Над странита HJ, конструиран е триаголник HJI кој е складен со триаголникот ABC, но заротиран за 180 ° (степени) во однос на него.
- Шестаголникот AJIHBC се преполовува со неговата дијагонала CI.
- Со поврзување на точките Е и F се добива шестаголник ABGFED кој се преполовува со својата дијагонала DG. Триаголниците ABC и ECF се симетрични во однос на дијагоналата DG, што што за последица има точките D, C и G да се колинеарни.
- Ако четириаголникот DABG се заротира околу точката A за 90° (во насока на стрелките на часовникот на приложената слика), тој ќе се совпадне со четириаголникот CAJI, што значи дека тие имаат еднакви плоштини. Ова е последица на тоа што аглите DAC и BAJ се прави, што значи дека аголот DAB е еднаков на аголот CAJ, бидејќи и двата се еднакви на збирот на правиот агол и аголот CAB. Слично на тоа, аголот AJI е еднаков на аголот ABG, бидејќи и двата се еднакви на збирот на правиот агол и ABC аголот. Ова значи дека отсечката AD преминува во AC, отсечката AB преминува во AI, а отсечката BG во JI.
- Бидејќи четириаголниците DABG и CAJI имаат еднакви плоштини (да речеме, S), и шестаголници ABGFED и AJIHBC имаат меѓусебно еднакви плоштини (2S). Ако од шестаголникот ABGFED се изостават складните триаголници ABC и ECF, неговата плоштина се намалува на збирот на плоштините на квадратите ACED и BCFG. Од друга страна, ако плоштините на складните триаголници ABC и HJI, се одземат од плоштината на шестаголникот AJIHBC, добиената површина е еднаква на плоштината на квадратот ABHJ, а оттаму непосредно следи еднаквоста AC²+BC²=AB².
Доказот на Џорџ Ејри[уреди | уреди извор]

Англискиот математичар и астроном, Џорџ Бидел Ејри, го формулирал својот доказ во стих што бил испишан на придружната слика, а изворно гласи:
I am, as you can see,
a² + b² - ab
When two triangles on me stand,
Square of hypothenuse is plann'd
But if I stand on them instead
The squares of both sides are read.[30]
што на македонски може да се преведе со:
- „Јас сум, како што се гледа, a² + b² - ab. Кога на мене стојат два триаголници, се добива квадрат над хипотенузата. Но, ако застанам на нив, се добиваат квадрати над катетите.“
Идејата на доказот е да се забележи белиот петаголник кој е заеднички елемент за двете страни на равенката. На приложената слика е добиено така што квадратот на страната a и квадратот на страната b, се ставаат на иста линија и се потпираат еден на друг, а потоа се одземаат два сини правоаголни триаголници чии катети се со должини a и b. Плоштината на тој петаголник е точно a² + b² - ab. Ако му се додадат два црвени триаголници што се совпаѓаат со сините триаголници, плоштината на таа втора фигура ќе биде c², со што теоремата е докажана.
Обопштување на теоремата[уреди | уреди извор]
Косинусна теорема[уреди | уреди извор]

Едно од значајните обопшување на Питагоровата теорема е косинусната теорема, која, покрај за правоаголните, важи и за острите и тапите триаголници, односно може да се примени на кој било триаголник. Ако темињата, страните и аглите на триаголникот се означени како на сликата, важат еднаквостите:
Собирокот на вишокот може да се толкува како двоен скаларен производ на векторите определени од соодветните страни. Кога е прав агол, ќе биде , па тогаш последната еднаквост се сведува на Питагоровата теорема.
Просторна Питагорова теорема[уреди | уреди извор]
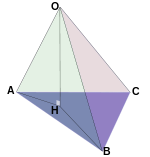
Еден просторен аналог на Питагоровата теорема е посебен случај на косинусната теорема за тетраедар, според кој, за површините на страните на тетраедарот означени со , , и , кои се спротивни на соодветните темиња во нивниот индекс, а за диедарските агли на рабовите (диедрален агол ???), (???) и (???), важи еднаквоста:
Ако аглите , и се прави, така што триедарот при темето е правоаголен, претходната еднаквост се сведува на:
што може да се смета за обопштување на Питагоровата теорема во просторот . Оваа теорема била претставена на Париската академија на науките од францускиот математичар Жан-Пол де Ги де Малвес во 1783 година, заради што го носи неговото име, иако истото веќе му било познато на Декарт.[33]
Парсевалова еднаквост[уреди | уреди извор]
Обопштувањето на Питагоровата теорема до бесконечнодимензионални сепарабилни предхилбертови простори е познато како Парсевалова еднаквост. Ако е еден таков простор, а еден од неговите ортонормални основи, потоа за секој вектор важи:
- [20] .
Последици и употреба на теоремата[уреди | уреди извор]
Питагорови тројки[уреди | уреди извор]
Питагоровата тројка е подредена тројка од природни броеви, и за која важи еднаквоста ²+²=², односно, Питагоровата тројка се состои од целобројните должини на страните на правоаголен триаголник. Вавилонски глинени плочи [34] ( англиски: YBC 7289, Plimpton 322) датирани 1800-1600 г. пр. н. е. покажуваат дека таквите тројки биле познати многу пред Питагора. Денес не е баш јасно каква употребна вредност имало тоа знаење. Според некои извори[35], се чини дека тоа е список на готови решенија за проблем што му овозможил на еден древен предавач по математика веднаш да ја провери точноста на ученичките трудови без дополнителни пресметки.
Секоја Питагорова тројка е со облик (ka, kb, kc), каде kе природен број, а (a, b, c) е примитивна Питагорова тројка (односно сочинуваат заемно прости броеви). Има бесконечно многу различни примитивни Питагорови тројки и позната е нивната експлицитна параметризација.
Геометриска конструкција на ирационални броеви[уреди | уреди извор]
Откривањето на ирационалните броеви им се припишува на питагорејците, но не е точно познато дали до нив стигнале со проучување на геометриската средина или со разгледување на должината на дијагоналата на квадрат.[36] Покрај тоа што утврдиле дека постојат несомерливи броеви, покажале дека тие можат да се конструираат, што сериозно го загрозило нивното верување дека во основата на сè е она што сега се нарекува рационален број, па откритието било строго чувано. Постои предание дека еден од членовите на братството, кој се осмелил јавно да проговори за тоа, за казна бил удавен во морето.[37]
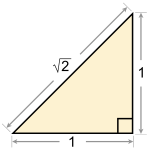
Иако тие не можат да се изразат како количник од два цели броја, некои ирационални броеви може да се конструираат со помош на линијар и шестар. Така, √2, која понекогаш се нарекува Питагорова константа [38], може да се добие како хипотенуза на правоаголен триаголник со двете катети со единица должина. Ако катетите се со должина 1 и √2, хипотенузата ќе биде со должина √3 и слично за квадратен корен од кој било природен број.
Не може сите позитивни ирационални броеви да се конструираат со помош на линијар и шестар. Конструктибилните броеви сочинуваат посебно подмножество од множеството алгебарски броеви и затоа ги има преброиво многу, додека останатите, неконструктибилни реални броеви ги има непреброиво многу. Неконструктибилни се на пример броевите .
Базелски проблем[уреди | уреди извор]
Италијанскиот математичар Пјетро Менголи во 1644 година го поставил прашањето за определување на збирот на реципрочните вредности на квадратите на сите природни броеви. Иако поставувањето на проблемот е релативно едноставно, решението се чекало речиси еден век, бидејќи Ојлер дури во 1735 година го објавил резултатот, за кој во 1741 година и докажал дека навистина е бараниот збир. Со помош на математичка нотација, базелскиот проблем може да се напише на следниов начин:
а збирот на дадениот ред може геометриски да се апроксимира со помош на Питагоровата теорема. Со конструирање правоаголен триаголник со катети со должина 1 и 1/2 се добива хипотенуза чија должина е квадратен корен од збирот на првите два члена од дадениот ред. Ако потоа се конструира нов правоаголен триаголник над таа хипотенуза како катета, чија втора катета со должина 1/3, неговата хипотенуза ќе има должина еднаква на квадратниот корен од збирот на првите три члена на истиот ред. Со проширување на постапката до бесконечност, должината на хипотенузата на секој следен триаголник е сè поблиску и поблиску до вредноста .
Растојанието помеѓу две точки во аналитичката геометрија[уреди | уреди извор]
Формулата за растојанието помеѓу две точки во Декартовиот правоаголен координатен систем е изведена со помош на Питагоровата теорема. Ако се и две точки во рамнината, тогаш нивното Евклидово растојание е:
Во општ случај, во повеќедимензионалниот Евклидов простор, растојанието помеѓу точките и се одредува со формулата:
Фермаовата последна теорема[уреди | уреди извор]
Последната Фермаова теорема е тврдење што Пјер де Ферма ја запишал без доказ на маргините на втората Диофантова книга Аритметика, а се однесува на прашањето дали постојат природни броеви што би го задоволиле обопштувањето на равенката со која се дефинираат Питагоровите тројки. Тврдењето до кое дошол околу 1637 година,[40] дека не постојат природни броеви за кои важи еднаквоста:
секогаш кога природниот број е поголем од 2, е претпоставка со векови, но тоа било докажано дури во 1995 година од Ендрју Вајлс.
Обратна Питагорова теорема[уреди | уреди извор]
Таканаречената Обратна Питагорова теорема гласи: Ако плоштината на квадратот конструиран над хипотенузата е еднаков на збирот на плоштините на квадратите конструирани над катетите, тогаш триаголникот е правоаголен.
Спомнување на Питагоровата теорема во општата култура[уреди | уреди извор]
Во книгата Автобиографија, Бранислав Нушиќ ја наведува формулацијата во стих:
Квадрат од хипотенузе,
То зна свако дете,
Раван је квадратима
Од обе катете.[41]
што на македонски би било:
Квадратот над хипотенузата,
Знае секое дете,
Еднаков е на квадратите
Над двете катети.
Германскиот поет и ботаничар, Аделберт фон Шамисо, посветил една од своите песни на откривањето на Питагоровата теорема.[42]
На една од седумте слики на францускиот сликар Лоран де ла Ер (француски: Laurent de La Hyre) што ги претставува седумте слободни вештини, древниот тривиум и квадривиум, под назив Алегорија на геометријата, е прикажана жена која држи пергамент со неколку геометриски фигури во десната рака.[43] Првата во серијата е токму сликата што Евклид ја дал во својот доказ за Питагоровата теорема во првата книга на Елементите.[21]
Во филмот на Виктор Флеминг „Волшебникот од Оз“, заснован на истоимената книга на Л. Френк Баум, постои сцена[44] во која еден од главните ликови, Страшилото, во мигот кога на подарок од Волшебникот добива диплома, го покажува своето знаење со експлицитно наведување на неточна изјава на теоремата во следниов облик:
Збирот на квадратните корени на кои било страни на рамнокрак триаголник е еднаков на квадратниот корен на третата страна.[45]
Формулацијата на Страшилото ја наведува Хомер Симпсон во десеттата епизода од петтата серија на „Симпсонови“, откако ги употребил очилата на Хенри Кисинџер пронајдени во тоалетот на Спрингфилдската нуклеарна електрана. За разлика од исказот на Страшилото, кој останува неточен, во цртаната серија, од позадина се слуша глас кој делумно го поправа Хомер („Тоа е правоаголен триаголник, идиот.“).[46]
Во Грција, Јапонија, Сан Марино, Македонија и Суринам биле издадени поштенски марки со визуелен приказ на Питагоровата теорема.[47]
Во Уганда во 2000 година во оптек била монета во облик на правоаголен триаголник, на чија задна страна е фигурата на Питагора и алгебарската нотација на теоремата, заедно со текстот „Питагоров милениум“.[48]
Слика што ја симболизира Питагоровата теорема може да се види и на грбот на шведскиот инженер Кристофер Полхем (шведски: Christopher Polhem).[49]
Во седумнаесеттата и триесет и четвртата книга на англиското издание на стрипот Астерикс се појавува ликот на младиот римски архитект Квадратнадхипотенузис (англиски: Squareonthehypothenus), чие име е вдахновено од теоремата.[50]
Наводи[уреди | уреди извор]
- ↑ Heath,, pp. 144
- ↑ Миланковић 2017.
- ↑ Логос 2017.
- ↑ Андрић 1989.
- ↑ 5,0 5,1 Smith,, pp. 288
- ↑ Стројк, Кратак преглед историје математике, pp. 21
- ↑ Maor,, pp. 15
- ↑ Maor, The Pythagorean Theorem - A 4000 Year History, pp. 17.
- ↑ Стројк, Кратак преглед историје математике, pp. 52
- ↑ 10,0 10,1 Maor, The Pythagorean Theorem - A 4000 Year History, pp. 42.
- ↑ Burton 2005.
- ↑ „Pythagoras - 5. Was Pythagoras a Mathematician or Cosmologist?“. Посетено на 22. 3. 2009. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ Лучић 2009.
- ↑ Митровић 1988.
- ↑ Због недостатка извора тешко је одредити када се то тачно десило. Према књизи у питању је период између 100. п. н. е. и 100. године н. е.
- ↑ Дугошија 1999.
- ↑ Оваа еднаквост се добива како специјален случај на косинусната теорема за сферен триаголник. Доколку косинусната функција се развие со помош на Маклореновиот ред, можно е да се покаже дека наведениот облик на Питагоровата теорема ќе се приближува на својот евклидски еквивалент кога полупречникот на сферата тежи кон бескончност.
- ↑ Stahl, Saul (1993). „Theorem 8.3“. The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. ISBN 978-0-86720-298-4.
За доказ погледати „Sines and cosines in the Poincar´e disk model of the hyperbolic plane“ (PDF). стр. 122. Посетено на 24. 2. 2009. Проверете ги датумските вредности во:|accessdate=(help) - ↑ За особине погледати Д. Аднађевић, З. Каделбург,Математичка анализа , pp. 268
- ↑ 20,0 20,1 Каделбург 1991
- ↑ 21,0 21,1 21,2 21,3 21,4 21,5 Maor, The Pythagorean Theorem - A 4000 Year History
- ↑ Еуклид, Елементи, књига, тврђење , Приступљено 23. 4. 2013.
- ↑ 23,0 23,1 Еуклид, Елементи, књига, тврђење , Приступљено 23. 4. 2013.
- ↑ Евклид, Елементи, книга, тврдење , Пристапено 23. 4. 2013.
- ↑ Евклид, Елементи, книга, тврдење , Пристапено 23. 4. 2013.
- ↑ Ради једноставнијег праћења доказа погледати следећи визуелни доказ, трансформацију приказану помоћу јава-аплета, и анимацију.
- ↑ Еуклид, Елементи, књига, тврђење , Приступљено 23. 4. 2013.
- ↑ Петковић 2006.
- ↑ Ради једноставнијег праћења доказа погледати следећу анимацију и архивиранутрансформацију коју је могуће интерактивно направити уз подршку јава-аплета.
- ↑ „Још један врло једноставан доказ“. Посетено на 22. 11. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ Дугошија, Ивановић & Милин 1999.
- ↑ „Милорад Бељић, Косинусна теорема за тетраедар“ (PDF). Посетено на 23. 10. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ „de Gua's Theorem“. Посетено на 23. 10. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ Видети 7289 и 322
- ↑ „Eleanor Robson, Words and Pictures: New Light on Plimpton 322“ (PDF). Посетено на 16. 11. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ Стројк, Кратак преглед историје математике, pp. 53
- ↑ Heath, A History Of Greek Mathematics, volume I, pp. 154.
- ↑ Finch 2003.
- ↑ Кечкић 1994.
- ↑ Синг 1999.
- ↑ Нушић 1963, стр. 125,127.
- ↑ Погледати оригинални текст на немачком, и превод на енглески Брајана Кола: „Adalbert von Chamisso, Vom Pythagoreischen Lehrsatz“. Архивирано од изворникот на 26. 3. 2012. Посетено на 22. 11. 2008. Проверете ги датумските вредности во:
|accessdate=, |archive-date=(help) - ↑ „Laurent de La Hyre (1601—1666), Allegory of Geometry“. Архивирано од изворникот на 07. 03. 2016. Посетено на 16. 11. 2008. Проверете ги датумските вредности во:
|accessdate=, |archive-date=(help) - ↑ „Wizard of Oz, Scarecrow's Mathematical Error“. Посетено на 5. 8. 2017. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ „Реплике Страшила из филма „Чаробњак из Оза"“. Посетено на 15. 11. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ „Реплике Симпсонових из епизоде „$прингфилд"“. Посетено на 15. 11. 2008. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ Miller, Jeff. „Images of Mathematicians on Postage Stamps“. Посетено на 20. 4. 2014. Проверете ги датумските вредности во:
|accessdate=(help)
Погледати поштанске марке издате у Грчкој, Јапану, Сан Марину, Македонији и Суринаму. - ↑ „Le Saviez-vous?“. Архивирано од изворникот на 21. 9. 2009. Посетено на 7. 10. 2008. Проверете ги датумските вредности во:
|accessdate=, |archive-date=(help) - ↑ „Christopher Polhem (1661-1751).Swedish engineer, knighted in 1716“. Посетено на 24. 2. 2009. Проверете ги датумските вредности во:
|accessdate=(help) - ↑ „Squareonthehypothenus“. Архивирано од изворникот на 20. 11. 2010. Посетено на 20. 2. 2011. Проверете ги датумските вредности во:
|accessdate=, |archive-date=(help)



































![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)








