Тетраедар
| Правилен тетраедар | |
|---|---|
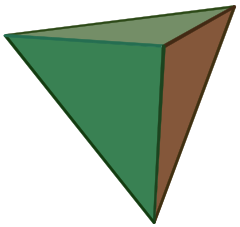 (вртечки модел) | |
| Тип | правилен полиедар |
| Елементи | F = 4, E = 6 V = 4 (χ = 2) |
| Страни | 4{3} |
| Шлефлиев симбол | {3,3} и s{2,2} |
| Витхофов симбол | 3 | 2 3 | 2 2 2 |
| Коксетер–Динкин | |
| Симетрија | Td, A3, [3,3], (*332) |
| Вртежна група | T, [3,3]+, (332) |
| Наводи | U01, C15, W1 |
| Својства | правилен испакнат |
| Диедарски агол | 70,528779° = arccos(1/3) |
 3.3.3 (темена фигура) |
 самодуално (дуален полиедар) |
 мрежа | |
Тетраедарот е полиедар составен од четири триаголни страни, од кои три се среќаваат во секое теме. Има шест рабови и четири темиња. Тетраедарот е единствениот испакнат (конексен) полиедар што има четири страни.[1] Ова тело претставува тридимензионален случај на поопштиот концепт на симплексот.
Тетраедарот е вид на пирамида, која е полиедар со рамна многуаголна основа и триаголни страни што ја поврзуваат во заедничка точка. Кај тетраедарот, основата е триаголна (било која од четирите страни), па затоа се нарекува и „триаголна пирамида“.[2] Како и сите испакнати полиедри, тетраедарот може да се превитка од еден лист хартија. Има две мрежи.[1]
За секој тетраедар постои сфера на чија површина лежат неговите темиња (опишана сфера).
Посебни случаи[уреди | уреди извор]
Правилен тетраедар е оној каде сите четири страни се рамнострани триаголници, и претставува едно од Платонските тела (правилни полиедри). Рамнокрак тетраедар (дисфеноид) е тетраедар каде сите четири страни се триаголници што се сечат во една точка. Кај триправоаголниот тетраедар, трите страни во темето имаат прави агли. Ако сите три пара на спротивни рабови се правоаголни, тогаш ова ќе биде ортоцентарски тетраедар. Кога истото важи само за еден пар, тоа се нарекува полуортоцентричен тетраедар.
Формули за правилен тетраедар[уреди | уреди извор]
Следниве Декартови координати ги дефинираат четирите темиња на тетраедарот со раб со должина 2, и а сосредоточен во координатниот почеток:
- (±1, 0, -1/√2)
- (0, ±1, 1/√2)
За правилен тетраедар со раб a:
| Плоштина на основата | |
| Плоштина[3] | |
| Висина[4] | |
| Волумен[3] | |
| Агол помеѓу раб и страна | (прибл. 54,7356°) |
| Агол помеѓу две страни[3] | (прибл. 70,5288°) |
| Агол помеѓу отсечките што ги поврзуваат центарот и темињата,[5] наречен и „тетраедарски агол“ | (прибл. 109,4712°) |
| Просторен агол на темето опфатено од страна | (прибл. 0,55129 стерадијани) |
| Полупречник на опишана сефера[3] | |
| Полупречник на впишана сфера тангентна на страните[3] | |
| Полупречник на полувпишана сфера тангентна на рабовите[3] | |
| Полупречник на опишаните сфери | |
| Растојание до центарот на опишаната сфера од темето |
Треба да се напомене дека, во однос на основната рамнина, коефициентот на правата (косината) на страната () е двапати поголема од онаа на работ (), што одговара на фактот дека хоризонталното растојание од основата до темето долж работ е двојно поголемо од она долж медијаната на страната. Со други зборови, ако C е тежиштето на основата, растојанието од C до темето на основата е двапати поголемо од растојанието од C до средишната точка на раб на основата. Ова се должи на тоа дека медијаните на еден триаголник се сечат во неговото тежиште, и дека оваа точка ги дели на две отсечки, од кои едната е двапати подолга од другата.
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ 1,0 1,1 „Тетраедар“ од Ерик В. Вајсштајн — MathWorld (англиски)
- ↑ „тетраедар“ — Лексикон на македонскиот јазик
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ↑ Köller, Jürgen, "Tetrahedron", Mathematische Basteleien, 2001
- ↑ Агол помеѓу два крака на тетраедарот Архивирано на 3 октомври 2018 г. - Maze5.net (англиски)
Надворешни врски[уреди | уреди извор]
| „Тетраедар“ на Ризницата ? |
- „Ојлерови точки“ од Ерик В. Вајсштајн — MathWorld (англиски)
- Richard Klitzing, 3D convex uniform polyhedra, x3o3o - tet
- Правилни полиедри (англиски)















