Кориолисова сила

Кориолисова сила (или Кориолисов ефект) — закривување на предметите во движење кога тие се разгледуваат во вртежен појдовен систем. Во појдовен систем со вртење во насока на стрелките на часовникот, закривеноста е на лево од движењето на предметот, додека пак вртењето во насоката спротивна на насоката на стрелките на часовникот, закривеноста ќе биде кон десно. Иако препознаена од останатите, математичкиот израз за Кориолисовата сила се појавува првпат во научна статија во 1835 година напишана од францускиот научник Гаспар-Гистав Кориолис, како дел од теоријата за воденичарски тркала. Во почетоците на XX век, поимот Кориолисова сила почнал да се употребува во поврзаност со метеорологијата.
Њутновите закони за движењето го опишуваат движењето на предметите во (незабрзувачки) инерцијални системи. Кога Њутновите закони се пренесени во истовремен вртежен појдовен систем, се појавуваат Кориолисовата и центрифугалната сила. Двете сили се пропорционални во однос на масата на предметот. Кориолисовата сила е пропорционална на стапката на вртење, а центрифугалната сила е пропорционална на квадратот на тоа движење. Кориолисовата сила дејствува во насока нормална на оската на вртење и брзината на телото во вртежен систем и е пропорционална на брзината на предметот во вртежен систем. Центрифугалната сила дејствува нанадвор во радијална насока и е пропорционална на растојанието на телото од оската на вртежниот систем. Овие дополнителни сили се наречени инерцијални сили, замислени сили или „псевдосили“.[1] Нив ги дозволуваат Њутновите закони за вртежни системи. Тие се чинителите на исправка кои не постојат при незабрзувачки или инерцијални појдовни системи.
Секако, најчесто наведуван вртежен појдовен систем е Земјата. Кориолисовиот ефект е предизвикан од вртењето на Земјата и инерцијата на масата која е под дејството на ефектот. Бидејќи Земјата завршува едно свртување на ден, Кориолисовата силе е многу мала, и ефектите се општо забележливи за движењата кои се случуваат на поголеми растојанија и при долгорочни временски периоди, како што се движењата на воздухот во атмосферата и водата во океаните. Овие движења се попречени од површината на Земјата, па затоа само се користи хоризонталната компонента на Кориолисовата сила. Оваа сила предизвикува предметите кои се движат на површината на Земјата да се движат по закривени во насока на движењето на стрелките на часовникот (во однос на насоката на движењето) во северната полутопка и во насока спротивна на часовникот во јужната полутопка. Наместо да се движат ветриштата и струењата линиски од области со висок притисок кон области со низок притисок, како што би бил случајот во невртежен систем, ветриштата и струењата се движат кон десно на северната страна од екваторот и на лево од јужната страна на екваторот. Овој ефект е одговорен за вртењето на големите циклони (видете Кориолисовиот ефект во метеорологијата).
Историја[уреди | уреди извор]
Италијанските научници Џовани Батиста Ричоли и неговиот помошник Франческо Марија Грималди го опишале ефектот во поврзаност со артилеријата 1651 година Almagestum Novum, пишувајќи дека вртењето на Земјата би требало да предизвика ѓулето испукано од север да закриви со насоката кон исток.[2] Истиот ефект бил опишан и во плимните равенки од страна на Пјер-Симон Лаплас во 1778 година.
Гаспар-Гистав Кориолис го објавил својот труд во 1835 година за енергетскиот придонес на машините со вртежни делови, како што се воденичарските тркала.[3] Во овој труд се разгледуваа дополнителните сили кои се присутни во вртежен појдовен систем. Кориолис ги поделил овие дополнителни сили во две категории. Втората категорија содржела сила која потекнува од накрсниот производ на аголната брзина на координатниот систем и проекцијата на брзината на предметот во рамнина нормална на оската на вртење. Кориолис ја означил оваа сила како „компактна центрифугална сила“ поради сличноста со центрифугалната сила која веќе била присутна во првата категорија.[4][5] Ефектот бил познат на почетокот на XX век како „забрзување на Кориолис“,[6] а од 1920 како „Кориолисова сила“.[7]
Во 1856 година, Вилјам Ферел го предложил постоењето на циркулациона ќелија во средните височини на атмосферата каде воздухот под дејство на Кориолисовата сила создава преовладувачки западни ветришта.[8]
Познавањето на кинематиката како точно вртењето на Земјата влијае на протокот на воздухот било делумно разбран.[9] Подоцна при крајот на XIX век, било согледано огромното ниво на кое заемодејствуваат градиентот на силата на притисокот и силата на закривување која предизвикува воздушните маси да се движат 'по' изобари.
Равенка[уреди | уреди извор]
Користејќи векторски поими: при одредено вртење на набљудувачот, големината на Кориолисовото забрзување на предметот е пропорционално на брзината на предметот и со синусот од аголот помеѓу насоката на движење на предметот и оската на вртење.
Векторската формула за големината и насоката на Кориолисовото забрзување [10] е :
каде (горе и подолу) е забрзувањето на честичката во вртежниот систем, е брзината на честичката во вртежниот систем и Ω е аголната брзина, вектор кој има големина еднаква на чекорот на вртење ω и е насочен долж оската на вртење на вртежниот појдовен систем и × го претставува операторот накрсен производ.
Равенката може да се помножи со масата на предметот и да се добие Кориолисовата сила:
- .
Погледај замислена сила за тоа како се изведува равенката.
Кориолисовиот ефект е појавата која се должи на Кориолисовото забрзување. Равенката тврди дека Кориолисовото забрзување е нормално и на насоката на брзината на масата која се движи и на оската на вртење на системот. Па важат следниве тврдења:
- Ако брзината е паралелна на вртежната оска, Кориолисовото забрзување е нула.
- Ако брзината е насочена право навнатре кон оската, забрзувањето е во насоката на правецот на вртење.
- Ако брзината е насочена право нанадвор кон оската, забрзувањето е спротивно на насоката на вртењето.
- Ако брзината е насочена кон насоката на вртењето, забрзувањето е насочено нанадвор од оската.
- Ако брзината е спротивна на насоката на вртењето, забрзувањето е насочено навнатре кон оската.
Векторскиот накрсен производ може да се пресмета како детерминанта на матрица:
каде векторите i, j, k се единечни вектори во насоките x, y и z.
Причини[уреди | уреди извор]
Кориолисовиот ефект се случува само кога се користи вртежен појдовен систем. Во вртежниот систем ефектот се однесува како вистинска сила (може да се каже, предизвикува забрзување и предизвикува вистински последици). Но, Кориолисовата сила е последица на инерцијата, и не е карактеристична за кое и да било тело, како што е случајот со електромагнетните и јадрените сили. Од аналитичка гледна точка, за да се искористи Њутновиот втор закон во вртежен систем, потребно е математички да се воведе и Кориолисовата сила, но истата отсуствува во незабрзувачки инерцијални појдовни системи. На пример, замислете си две деца на спротивните страни на рингишпил, кои си додаваат топка едно на друго. Од гледна точка на децата, патот на топката е закривен под дејство на Кориолисовиот ефект. Да си замислиме дека рингишпилот се врти во спротивна на часовникот гледано одгоре. Од гледна точка на фрлачот патеката е закривена кон десно.[11] Од гледната точка на оној кој ја чека топката, истата закривува кон лево. За математичкиот запис погледај математичко изведување на замислени сили.
Набљудувач во вртежен систем, како на пример астронаут во вртежна вселенска станица, мошне полесно ќе го согледа однесувањето на Кориолисовата сила низ секојдневниот живот отколку да се занимава со математичко размислување од гледна точка на појдовни системи. На пример, гадењето е предизвикано од движењата кои полесно би се објасниле со Кориолисовата сила отколку со законот за инерција.[12][13] Погледај исто така за Кориолисов ефект (восприемање). Во метеорологијата, вртежниот систем (Земјата) во заедништво со Кориолисовата сила претставува поприроден систем за објаснување на движењето на воздухот чие придвижување не би можело да се објасни со невртежен со отсуство на Кориолисови сили појдовен систем.[14] При прецизната далекустрелна артилерија, исправките на нишанењето поради Земјиното вртење се поради Кориолисовата сила.[15] Примерите за овие тврдења се опишани подолу во статијата.
Забрзувањето кое е дел од Кориолисовата сила потекнува од два извори на промена на брзината како резултат од вртењето: првиот е промената на брзината на предметот со текот на времето. Истата брзина (во инерцијален појдовен систем каде што важат нормалните закони на физиката) во кружниот појдовен систем ќе има различни брзини во различни временски периоди. Забрзувањето е пропорционално со аголната брзина на појдовниот систем (стапката со која координатните оски ја менуваат насоката), и компонентата на брзината на предметот во рамнина нормална на оската на вртење. Одовде се добива израз . Минусниот знак потекнува од традиционалната дефиниција на накрсниот производ (правило на десна рака) и од правилата за записи на векторите на аголната брзина.
Вториот е промената на брзината во просторот. Различни положби во вртежниот појдовен систем имаат различни брзини (како што може да се види и од инерцијалниот појдовен систем). За да еден предмет се движи по права линија мора истиот да се забрзува од точка во точка со иста брзина како и брзината на појдовниот систем. Ефектот е пропорционален на аголната брзина (која пак ја одредува релативната брзина на две различни точки во вртежниот појдовен систем), и со компонентата на брзината на предметот во рамнината нормална на оската на вртење (која одредува колку брзо се движи меѓу тие две точки). и одовде се добива изразот .
Должински величини и Росбиев број[уреди | уреди извор]
Временската, просторната и брзинската големина се од важност за определување на Кориолисовиот ефект. Дали вртењето е од важност за еден систем може да се утврди од Росбиевиот број, кој е односот од брзината, U, на системот и производот од Кориолисовиот параметар,, и од должинската големина, L, на движењето:
Росбиевиот број е односот на внатрешните Кориолисови сили. Мала вредност на Росбиевиот број означува систем кој е под силно дејство на Кориолисовите сили, Росбиев број со голема вредност означува систем каде преовладуваат инерцијалните сили. На пример, во торнадата,Росбиевиот број се одликува со голема вредност, додека во системите со низок притисок е со мала вредност, а пак во океанските системи вредноста му е 1. Како резултат на ова, Кориолисовите сили кај торнадата се занемарливи, и рамнотежата е меѓу притисокот и центрифугалните сили. Кај системите со низок притисок, центрифугалните сили се занемарливи а рамнотежата е меѓу Кориолисовите сили и притисокот. Кај океаните сите овие сили се подеднакво застапени.[16]
На атмосферски систем кој се движи со брзина U = 10 м/с и зафаќа просторно растојание од L = 1000 км, вредноста на Росбиевиот број му е 0,1. Фрлач на бејзбол топче може да ја фрли топката со брзина U = 45 м/с на растојание од L = 18,3 м. Вредноста на Росбиевиот број во овој случај ќе биде 32.000. Потребно е да се каже дека не треба да се грижиме на која полутопка сме кога играме бејзбол. Но, наведувана ракета се покорува на истите законитости како и бејзболот, но може да отпатува доволно далеку за да се појави ефектот на Кориолисовата сила. Далекустрелните гранати во северната полутопка паѓаат близу но на десно од метата сè до оној момент додека не се забележи влијанието на Кориолисовата сила. (Истреланите гранати на јужната полутопка паѓаа налево од метата.) Всушност, ова е ефектот кој и првично го поттикнал интересот за силата кај Кориолис.[17][18][19]
Примена на Земјата[уреди | уреди извор]
Важен случај за постоење на Кориолисовата сила е вртењето на Земјата. Доколку не е поинаку кажано, насоките и движењата се однесуваат на северната полутопка.
Интуитивно објаснување[уреди | уреди извор]
Како што Земјата се врти околу својата оска, се што е на нејзината површина се врти со самата Земја (незабележливо за нашите сетила). Предмет кој се движи без притоа да биде влечен под дејство на вртењето ќе се движи во права линија преку површината на Земјата која се врти. Од нашето гледиште на планетата, правецот на движењето на предметот ќе се менува како што истиот ќе се движи, накривувајќи се во спротивната насока од насоката на движењето. Кога би се гледал предметот од статична точка одозгора, сите релјефни одлики на северната полутопка ќе се движат во насока спротивна на насоката на движење на стрелките на часовникот, и сè додека го држиме нашиот поглед на таа местоположба, секоја останата местоположба на таа полутопка ќе се врти околу истата на истиот начин. Исцртаниот поминат пат на слободното подвижно тело кое патува од една до друга точка ќе се закривува во спротивата насока од насоката на движењето на стрелките на часовникот, насока која традиционално е наречена „десна“ (англиски: right, каде ќе биде ако насоката на движење се смета за „нанапред“ и „надолу“ исто така е дефинирана.
Топка во вртење[уреди | уреди извор]
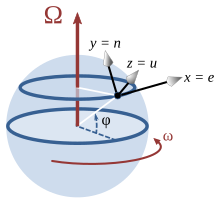
Ако се разгледува местоположба со ширина φ на топка која се врти околу северно-јужната оска.[20] Се поставува координатен систем со x оската хоризонтално кон исток, y оската хоризонтално кон север и z оската вертикално нагоре. Векторот на вртење, брзината на движењето t и Кориолисовото забрзување се изразени во овој координатен систем (наведувајќи ги компонентите по редоследот исток (e), север (n) и нагоре (u)) се:
Кога се разгледува атмосферска или динамика на океани, вертикалната компонента е мала а со тоа и вертикалната компонента на Кориолисовото забрзување е мала во споредба со гравитацијата. За ваквите случаи, од важност се само хоризонталните (источна и северна) компоненти. Ограничувањето од погоре спомнатото на хоризонталната рамнина е (случајот кога vu = 0):
каде е наречен Кориолисов параметар.
Случајот кога vn = 0, може веднаш да се забележи дека (за позитивни φ и ω) движењето кон исток ќе предизвика забрзување кон југ. Слично, случајот кога ve = 0, се набљудува дека придвижувањето кон север ќе предизвика забрзување кон исток. Општо, набљудувањата хоризонтално, гледајќи долж насоката на движењето предизвикува забрзување, забрзувањето секогаш скршнува за 90° кон десно со иста големина без разлика на поставеноста на хоризонталата.
Во поинаков случај, да се разгледува случај на екваторско движење φ = 0°. Во овој случај, Ω е паралелно со север или n-оската, и:
Соодветно, движење кон исток (поточно, во иста насока како и насоката на вртењето на топката) обезбедува нагорно забрзување познато како Етвешов ефект, и нагорното движење предизвикува забрзување насочено кон запад.
- За подетални примери во оваа статија погледај Топ на маса што се врти и Фрлена топка. Во други статии, погледај топки во вртење, очигледно движење на статични објекти, и рингишпил.
Далечни ѕвезди[уреди | уреди извор]
Очигледното движење на далечните ѕвезди гледано од Земјата е под влијание на Кориолисовите и центрифугалните сили. Замислете си таква ѕвезда (со маса м) со местоположба r, со деклинација δ, по Ω • r = |r| Ω sin(δ), каде Ω е вртежниот вектор на Земјата. За ѕвездата се знае дека се врти околу Земјината оска со период од еден сидерички ден во спротивна насока од таа на Земјиното вртење, со што нејзината брзина изнесува v = –Ω × r. замислената сила, која се состои од Кориолисови и центрифугални сили е:
каде uΩ = Ω−1Ω е единичен вектор во насока на Ω. Оваа замислена сила Ff е всушност вектор со големина m Ω2|r| cos(δ), нормален на Ω, и насочен кон центарот на ѕвезденото вртење на Земјината оска, сила позната како центрипетална сила која ќе ја задржува ѕвездата во кружно движење околу таа оска.
Метеорологија[уреди | уреди извор]



Можеби најважното влијание на Кориолисовиот ефект е делувањето на големите подвижни системи како што се океаните и атмосферата. Во метеорологијата и океанографијата, погодно е да се претпостави вртежен појдовен систем каде Земјата е статична. За да се исполни тој услов се воведуваат центрифугалната и Кориолисовта сила. Нивното релативно значење е определено од вредноста на Росбиевите броеви. Торнадата имаат висока вредност на Росбиевиот број, па, оттука центрифугалните сили поврзани со торнадата се силно изразени, додека пак Кориолисовите сили се занемарливи.[21]
Бидејќи струите настануваат под дејство на движењето на ветриштата над површината на океаните, Кориолисовиот ефект исто така влијае и на движењето на океанските струи а оттука и на ураганите. Многу од поголемите океански струи циркулираат во топлите области со висок воздушен притисок кои се наречени кружни форми (жиро). Иако циркулирањето не е од големо значење како кај воздухот, закривеноста непредизвикано од Кориолисовиот ефект е силата која ги создава спиралните движења во овие кружни форми. Спиралните движења на ветрот помагаат во создавањето на обликот на ураганите. Колку што е посилна силата на Кориолисовиот ефект, толку побрзо ќе се вртат и ветриштата и ќе собираат дополнителна енергија, со што се зголемува силата на ураганот.[22]
Воздухот во системите со висок притисок се врти во таква насока што Кориолисовата сила ќе биде насочена радијално навнатре, и скоро близу во рамнотежа со надворешно насочениот градиент на притисокот. Како резултат на ова, воздухот се движи во насока на часовникот околу областите со висок притисок во северната полутопка и во обратна од часовникот на јужната полутопка. Воздухот во областите со низок притисок се врти во спротивна насока, на тој начин што Кориолисовата сила е насочена радијално нанадвор и е скоро во рамнотежа со навнатре радијално насочен градиент на притисокот.
Ток и области со низок притисок[уреди | уреди извор]
Ако во атмосферата се создаде област со низок притисок, воздухот ќе почне да дотекува кон таа област, но ќе биде закривуван нормално на сопствената брзина под дејство на Кориолисовата сила. Во тој момент може да се создаде рамнотежен систем на кружно движење, или циклонски ток. Бидејќи Росбиевиот број има ниска вредност, рамнотежата на силите е меѓу силата на градиентот на притисокот која дејствува кон областа со низок притисок и Кориолисовата сола која дејствува нанадвор од центарот на областа со низок притисок.
Наместо да го следи градиентот по должина надолу, движењата на огромните површини како атмосферата и океаните се случуваат нормално на градиентот на притисокот. Ова е познато како геострофен ток.[23] На планета која не се врти, течностите би течеле по најправата можна линија, со што би се отстраниле градиентите на притисокот. Се забележува дека геострофната рамнотежа е многу поразлична од случајот кога имаме „инерцијални движења“ (погледај подолу) која објаснува зашто циклоните на средна ширина се поголеми по која било величина отколку тековите на инерцијалните кругови.
Оваа шема на закривување, и насоката на движење, е наречена Бејсбалотов закон. Во атмосферата, шемата на токот се нарекува циклон. На северната полутопка насоката на движењето околу областа со низок притисок е во насока спротивна на часовникот. На јужната полутопка, насоката на движење е спротивна на часовникот, бидејќи динамиката на вртењето е како огледална слика на северната полутопка. На големи височини, воздухот кој се шири врти во спротивна насока.[24] Циклоните ретко се формираат по должината на екваторот поради слабиот Кориолисов ефект присутен во овој регион.
Инерцијални кругови[уреди | уреди извор]
Воздушна или водена маса која се движи со брзина и е под дејство на Кориолисовата сила која се движи по кружна патека наречена 'инерцијален круг'. Бидејќи силата е насочена под прав агол на движењето на честичката, ќе се движи со постојана брзина околу круг чиј полупречник е даден со:
каде е Кориолисовиот параметар , воведен одозгора (каде е ширината). Времето потребно за масата да заврти цел круг е изразено со . Кориолисовиот параметар вообичаено има средноширинска вредност од околу 10−4 s−1, па оттука вообичаената атмосферска брзина е 10 м/с, а полупречникот е 100 км, со период од околу 17 часа. За океанска струја со вообичаена брзина од 10 см/с, полупречникот на инерцијалниот круг е 1 км. Овие инерцијални кругови се движат во насока часовникот на северната полутопка и во спротивна насока од часовникот на јужната полутопка.
Ако вртежниот систем е параболичен, тогаш е постојана и патеките се прави кругови. На планета која се врти, се менува со ширината и патеките на честичките не опишуваат правилни кругови. Бидејќи параметарот се менува како синус од ширината, полупречникот на осцилациите поврзани со дадена брзина се најмали на половите (ширина = ±90°), и се зголемуваат кон екваторот.[25]
Останати земјени ефекти[уреди | уреди извор]
Кориолисовиот ефект дејствува силно на големите океански и атмосферски циркулации, што води кон создавање на гломазни структури како што се високите струења и западните гранични струи. Овие појави се во геострофна рамнотежа, што означува дека Кориолисовата сила и силата на градиентот на притисокот се во рамнотежа. Кориолисовото забрзување е исто така одговорно за движењето на многу видови на бранови во океаните и во атмосферата, вклучувајќи ги тука Росбиевите бранови и Келвиновите бранови. Исто така од важност е и кај т.н. Екманова динамика на океанот, и во воспоставувањето на големиот океански ток наречен Свердрупова рамнотежа.
Етвешов ефект[уреди | уреди извор]
Практичното влијание на „Кориолисовиот ефект“ (англиски: Coriolis effect) е предизвикано од хоризонталното забрзување добиено како компонента на хоризонталното движење.
Постојат и други компоненти на Кориолисовиот ефект. Предметите кои се движат кон исток ќе бидат поместени нагоре (како да се полесни), додека предметите кои се движат кон запад ќе бидат поместени надолу (како да се потешки). Ова е познато како Етвешов ефект. Овој ефект е дел од Кориолисовиот ефект и е најизразен во близина на екваторот. Силата добиена од овој ефект е слична на хоризонталната компоненета, но поголемата вертикална сила поради гравитацијата и притисокот прави овој динамички ефект да не е неинтересен.
Во продолжение, предметите кои се движат нагоре или надолу ќе бидат поместени западно или источно соодветно на движењето. Овој ефект е исто така најизразен на екваторот. Бидејќи вертикалното движење е обично ограничено по големина и времетраење, големината на ефектот е помалку изразена и потребни се прецизни инструменти за да се забележи. Но, при големи промени на импулсот, како на пример кога се лансира вселенско возило во орбитата, ефектот станува значаен па најбрзиот и најекономичниот пат за лансирање во орбитата е оној кој е најблизу до екваторот со што патеката се закривува право кон исток.
Одводите кај кадите и талетите[уреди | уреди извор]
Наспроти општоприсутната заблуда, вртењето на водата во домашните бањи при нормални услови не е поврзана со Кориолисовиот ефект или пак вртењето на Земјата, и не постои споредлива разлика меѓу насоката на вртење во тоалетите на северната и јужната полутопка. Создавањето на вител над одводниот отвор може да се објасни со зачувувањето на аголниот момент: Полупречникот на вртењето се намалува како што водата се приближува до одводниот отвор, па стапката на вртење се зголемува, од истата причина поради која и лизгач на мраз ја зголемува својата брзина кога ги собира рацете кон телото. Секое вртење околу одводниот отвор кое е присутно на почетокот ќе станува поизразено како што водата се движи навнатре.
Само ако водата е многу мирна и ефектот на Земјиното вртење е побрз од ефектот на водата во однос на садот, и ако надворешните моменти на сила (како оние кои се предизвикани од текот на дното на нерамната површина) се доволно мали, Кориолисовиот ефект ќе ја одреди насоката на вртење на вителот. Без ваква внимателна подготовка, Кориолисовиот ефект можно е да биде потиснат од други движења во насоката на одведување[26] како и вртењето која е останата во водата [27] и од обликот на садот во кој е водата.[28] Покрај ова, идејата дека тоалетите и кадите се одводнуваат поинаку на северната и јужната полутопка е општоприсутно во неколку телевизиски програми и филмови како што се План за бегство, Непоканети гости, Симпсонови во епизодата „Барт против Австралија“, и Досиеја Х во епизодата „Рака која казнува“.[29] Неколку научни програми и написи, како и еден учебник за физика ги наведуваат овие примери.[30][31]
Во 1908 година, австрискиот физичар Отокар Тумрлирц опишал внимателни и делотворни опити кои го покажале ефектот на вртењето на Земјата на одведувањето на водата низ централен отвор.[32] Темата подоцна била спомената во познат напис во списанието природа, стастија во која се опишувал опит во кој сите останати сили на системот се отстранети со полнење на 1,8 м висок резервоар со 1100 л вода и истат се остава да отстои 24 часа (за да се дозволи движењето кое настанало поради полнењето на резервоарот да замре), во соба во која температурата е стабилизирана. Затката полека се отстранува, и ситни дрвца се користат за да се набљудува вртењето. За време на првите 12 до 15 минути, не се забележува никакво вртење. Подоцна, се појавува вител кој постојано започна да врти спроти часовникот (опитот бил изведен во Бостон, Масачусетс, на северната полутопка). Ова било повторено а резултатите биле усреднети за да се осигура вистинитоста на резултатите. Извештајот содржел податоци дека вителот се вртел со брзина, „околу 30.000 пати побрза од делотворното вртење на Земјата на 42° северна ширина (местоположбата на опитот)“. Ова покажува дека малото почетно завртување поради вртењето на Земјата е засилено од гравитациското одведување и зачувувањето на аголниот момент со што се создава брз вител кој може да се набљудува во грижливо контролирани лабораториски услови.[33][34]
Далекустрелни ракети и сателити[уреди | уреди извор]
Далекустрелните ракети и сателити опишуваат закривени патеки кога се цртаат на обичните светски карти најчесто бидејќи Земјата е сферична и најкусото растојание помеѓу две точки на површината на Земјата (наречен голем круг) најчесто не е права линија на овие карти. Секоја дводимензионална (рамна) карта не ја прикажува Земјината закривена (тридимензионална) површина. Вообичаено (а и во секојдневната употреба на пример е Меркаторовото проектирање), ова нарушување се зголемува со близината до половите. На северната полутопка на пример, далекустрелните ракети истрелани кон далечни мети и користејќи ја најкусaта можна патека (големиот круг) на овие карти ќе опишува патека северно по права линија до целта, за подоцна да заврти повторно назад кон екваторот. Ова се случува бидејќи ширините, кој се проектирани како прави хоризонтални линии на повеќето светски карти, се всушност кругови на површината на топката, кои стануваат помали како што се доближуваат до половите. Бидејќи се последица на сферичноста на Земјата, ова ќе биде вистина и доколку Земјата не би се вртела. Секако присутен е и Кориолисовиот ефект, но неговото дејство на патеката е многу помало.
Кориолисовите ефекти станаа важни во надворешна балистика за пресметување на патеките на артилериските гранати со многу долги патеки. Најпознат историски пример е парискиот топ, користен од Германците за време на Првата светска војна за бомбардирање на Париз на растојание од 120 км.
Специјални случаи[уреди | уреди извор]
Топ на маса што се врти[уреди | уреди извор]




Анимацијата на почетокот на оваа статија е класична илустрација на Кориолисовата сила. Друга визуелизација на Кориолисовата сила и центрифугалната сила е анимираниот видео запис.
Со познат полупречник R на масата која се врти во тоа видео, со чекорот на аголно вртење ω и брзината на ѓулето да е постојана v, може да се пресмета погодниот агол за нишанење θ за да се погоди метата на работ од масата која се врти.
Инерцијалниот појдовен систем дава само еден начин на кој би можел да се одговори ова прашање: да се пресмета времето до пресретнувањето, кое е tf = R / v . Потоа, масата се завртува за агол ω tf во ова време. Ако топот е насочен за агол θ = ω tf = ω R / v, тогаш ѓулето пристигнува на надворешноста во местоположбата 3 во исто врем како и метата.
Не постои решение со Кориолисовата сила кое ќе дојде толку едноставно до решението како во погорниот пример, па причината да се разгледува овој проблем е за да се претстави Кориолисовиот формализам во една лесно воочлива ситуација.
Патеката во инерцијалниот систем (означена со A) е права линија со радијален пат под агол θ. Оваа местоположба на ѓулето во (x, y) координатите во време t е:
Во системот на масата која се врти (означен со B), x- y оските се вртат со аголен чекор ω, па патеката станува:
и три примери од овој резултат се нацртани на оваа слика.
За да се одредат компонентите на забрзувањето, се користи општ израз од статијата за замислена сила:
во кое поимот Ω × vB е Кориолисовото забрзување и поимот во Ω × ( Ω × rB) е центрифугалното забрзување. Па резултатите се (нека α = θ − ωt):
се добива центрифугалното забрзување:
Исто:
Се добива Кориолисовото забрзување:
Овие забрзувања се прикажани во дијаграмите за одредени примери.
Се гледа дека Кориолисовото забрзување не само што го поништува центрифугалното забрзување, туку заедно тие обезбедуваат вкупно „центрипетално“ забрзување, радијална компонента на забрзувањето насочена кон центарот на вртењето:[35]
и уште една дополнителна компонента на забрзувањето, нормална на rB (t):
„Центрипеталната“ компонента на забрзувањето наликува на силата за кружно движење со полупречник rB, додека пак нормалната компонента е зависна од брзината, зголемувајќи се со радијалната брзина v и насочена кон десно од брзината. Состојбата може да се опише како кружно движење во заедништво со „очигледното Кориолисово забрзување“ од 2ωv. Но ова е грубо означување: точното обележување на вистинската центрипетална сила се однесува на локални појдовни системи кои ги користат насоките нормални и тангенцијални на патеката, а не координатите кои се однесуваат на оската на вртење.
Овие резултати исто така можат да се добијат директно со двостепен извод на изразот rB (t). Очигледно е дека и двата приоди покажуваат дека може да се започне од општиот израз за замислено забрзување од погоре и да се добијат патеките кои се прикажани овде. Но, почнувајќи од забрзувањето па одејќи до патеката е посложен начин отколку обратната процедура која беше користена во примерот, којашто, секако, е можна доколку се знае резултатот однапред.
Како резултат на оваа анализа се добива важен заклучок: сите замислени забрзувања мора да бидат вклучени во пресметките за да се одредат вистинските патеки. Всушност, покрај Кориолисовото забрзување, значајна улога има и центрифугалната сила. Лесно се добива впечатокот од разговорите за проблемот со топот, кои се однесуваат на Кориолисовиот ефект, дека Кориолисовата сила е единствениот факт којшто треба да биде разгледуван,[36] но тоа не е случајот.[37] Маса која се врти и за која Кориолисовата сила е единствениот чинител е параболичната маса што се врти. Нешто посложена ситуација е идеализираниот пример за летови на долги растојанија, каде центрифугалната сила на патеката и аеронаутичкиот потисок се во спротивставеност со гравитациското привлекување.[38][39]
Фрлено топче на рингишпил[уреди | уреди извор]
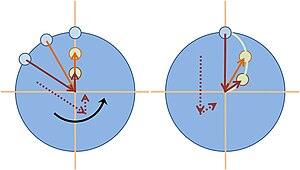
Сликата прикажува топка фрлена од метоположбата означена со 12:00 часот кон центарот на рингишпил кој врти спроти часовникот. На лево, топката е набљудувана од статичен набљудувач над рингишпилот, и топката се движи во права линија до центарот, додека пак фрлачот се врти спроти часовникот заедно со рингишпилот. На десно топката е набљудувана од набљудувачот кој се врти со рингишпилот, па изгледа како набљудувачот да стои на местоположбата во 12:00 часот. Сликата ја прикажува патеката на топката од гледната точка на набљудувачот кој се врти.
На лево, две стрелки ја покажуваат топката во однос на фрлачот. Една од овие стрелки е насочена од фрлачот кон центарот на рингишпилот, а другата е насочена од центарот на рингишпилот кон топката. променетите насоки на ситуациите се забележани со испрекинати линии.
На десно се прикажува истиот испрекинат пар на стрелки, но сега парот се врти со стрелките кои се соодветни на со линијата на гледање на фрлачот кон центарот на рингишпилот кој е подреден со 12:00 часот. Другата стрелка од парот ја покажува насоката на топката во однос на центарот на рингишпилот, со што се одредува местоположбата на топката гледана од фрлачот. Следејќи ја постапката за неколку местоположби, претставена е патеката во вртежниот појдовен систем како што е прикажано со закривена патека на десниот приказ на сликата.
Топката патува низ воздухот, и нема вкупна сила која влијае на неа. За статичниот набљудувач топката следи патека по права линија, па не постои проблем да се квадрира оваа патека со збирна сила еднаква на нула. Но, набљудувачот кој се врти гледа закривена патека. Во кинематиката мора да има сила која ќе го предизвика ова закривување, па вртежен набљудувач мора да се повика на збир од центрифугални и Кориолисови сили за да обезбеди збирна сила потребна за да се предизвика закривеноста на патеката.
Одбиена топка[уреди | уреди извор]

Сликата опишува посложена ситуација каде фрлената топка на маса која се врти се одбива од работ на рингишпилот и се враќа назад до фрлачот, кој ја фаќа топката. Ефектот на Кориолисовата сила на сопствената патека е прикажан повторно од двајца набљудувачи: набљудувач (кој се означува како „камера“) која се врти со рингишпилот, и статичен набљудувач. Сликата прикажува поглед од птичја перспектива која се заснова на истата брзина на топката при фрлањето и одбивањето на истата. Во секој од овие кругови, нацртаните точки ги покажуваат истите временски точки. На левиот приказ, од гледната точка на камерата во центарот на рингишпилот, фрлачот (насмеано лице) и оградата се на истите статични местоположби, и топката прави доста голем лак на нејзиниот пат до оградата, додека пак патеката на враќање е доста поедноставна. Од гледната точка на фрлачот, топката како да се враќа со поголема брзина од онаа со која била фрлена (бидејќи фрлачот се врти кон топката на нејзината патека назад).
На рингишпилот, наместо да се фрли топката право на оградата и да се одбие, фрлачот мора да ја фрли топката надесно од метата и топката тогаш на камерата и изгледа како да се движи постојано кон лево од нејзината насока на движење да ја удри оградата (лево бидејќи рингишпилот се врти во насока на часовникот). Топката изгледа како да се движи лево од насоката на патување на и при фрлањето и одбивањето. Закривената патека му покажува на набљудувачот дека постои вкупна сила која ја движи топката кон лево. (Оваа сила е „замислена“ бидејќи истата исчезнува за статичниот набљудувач, за што ќе се напомене подоцна.) За некои агли на лансирање, патеката има делови каде патеката е приближно радијална, и Кориолисовата сила е одговорна за привидното закривување на патеката на топката (центрифугалната сила е радијална од центарот на вртење, и предизвикува мало закривување во овие делови). Кога патеката закривува радијално, тогаш центрифугалната сила е одговорна за закривеноста.
Патеката на топката низ воздухот е права линија кога е гледана од набљудувачите кој стојат на земјата (десен приказ). На десниот приказ (статичниот набљудувач), фрлачот на топката (насмеаното лице) е на местоположбата во 12 часот и оградата од која топката се одбива е во местоположбата еден (1). Од гледната точка на статичниот набљудувач, местоположбите еден (1), два (2), три (3) се подредени по редослед. Во местоположбата 2 топката се судира со оградата, и во местоположбата 3 топката се враќа кон набљудувачот. Патеките се бидејќи топката е во слободен лет, па затоа за овој набљудувач не е потребно да се прави збир на сили.
Куршуми со големи брзини низ атмосферата[уреди | уреди извор]
Поради вртењето на Земјата, куршумите не се движат праволиниски од цевката до метата. Кориолисовиот ефект минимално ја менува патеката на куршумот, закривувајќи ја патеката на проектилот во патека којашто наликува на лак. Овој ефект ја опфаќа прецизноста на големи растојанија и тогаш е потребна д биде земена предвид од прецизните снајперисти и останатите тренирани професионалци.[15]
Визуелизација на Кориолисовиот ефект[уреди | уреди извор]

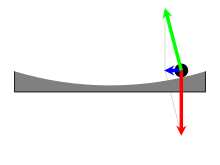
Црвена:гравитацијата
Зелена:нормална сила
Сина: резултантната центрипетална сила.

Лево: Поглед од статична точка.
Десно: од точка на заемно вртење.
за да се прикаже Кориолисовиот ефект, може да се искористи параболично вртежна маса. На рамна вртежна маса, инерцијата на предметот кој се врти со масата ќе биде исфрлен од работ. Но ако масата што се врти има параболоидна (параболичен сад) облик (погледај на сликата) и сè се врти со соодветен чекор, компонентите на силата прикажани на сликата се такви што компонентата на гравитација е тангенцијално на површината на садот точно ќе биде еднаква на центрипеталната сила потребна да се зачува предметот кој се врти со иста брзина и истиот полупречник на закривување (претпоставувајќи дека нема сила на триење). (погледај накосена кривина.) Оваа внимателно контурирана површина овозможува Кориолисовата сила да се прикажува во изолација.[40]
Дискови исечени од цилиндри сув мраз можат да се искористат како плочки за хокеј, движејќи се наоколу скоро без никакво триење на површината на параболичната маса што се врти, овозможувајќи да се набљудуваат динамичките појави на Кориолисовиот ефект. За да се има поглед на работите како што се гледа од вртежниот појдовен систем со масата во вртење, видеокамера е прикачена на масата во вртење за да биде во заемно вртење со истата, при што се добиваат резултатите прикажани на сликата. На левиот приказ од сликата, што всушност е гледиште на статичен набљудувач, гравитациската сила во инерцијалниот систем го влече предметот кон центарот (долу) на садот и е пропорционална со растојанието на предметот од центарот. Центрипетална сила со овој облик го предизвикува елиптичното движење. На десниот приказ, каде е прикажано гледиштето од системот кој се врти, внатрешно насочената гравитациска сила во системот на вртење (истата сила како и во инерцијалниот систем) е во рамнотежа со надворешно насочената центрифугална сила (присутна само во вртежни системи). Со овие две сили во рамнотежа, единствената сила која не е во рамнотежа е Кориолисовата сила (исто така присутна само во вртежен систем), а движењето е инерцијален круг. Анализа и набљудување на кружно движење во вртежен систем е поедноставување споредбено со елиптичното движење во инерцијалниот систем.
Бидејќи овој појдовен систем има неколку вртежи во минута, наместо еднаш дневно како Земјата, Кориолисовото забрзување кое се добива е многупати поголемо и полесно за набљудување во покуси временски периоди и просторни величини отколку кога Кориолисовото забрзување е предизвикано од вртењето на Земјата.
На некој начин, Земјата е слична на масата што се врти.[41] Вртењето предизвикало планетата да добие сферичен облик додека се ладела, на тој начин што нормалната сила, гравитациската сила и центрифугалната сила се во целосна рамнотежа едни со други на „хоризонтална“ површина. (Погледај екваторска испакнатост.)
Кориолисовиот ефект предизвикан од вртењето на Земјата може индиректно да се види преку движењето на Фукоовото нишало.
Кориолисови ефекти во други области[уреди | уреди извор]
Кориолисов протокомер[уреди | уреди извор]
Практична примена на Кориолисовиот ефект е зафатнинскиот протокомер, инструмент кој ја мери стапката на зафатнински проток и густината на течноста низ цевка. Начинот на работа вклучува предизвикување на вибрација во цевката низ која минува течноста. Вибрацијата иако не е целосно кружна, го обезбедува вртежниот појдовен систем кој го создава Кориолисовиот ефект. Иако има различни методи во зависност од дизајнот на протокомерот, отчитувачи ги следат и анализираат промените во честотата, фазата, и амплитудата на токот кој вибрира додека се движи низ цевката. Промените кои се набљудуваат го претставуваат зафатнинскиот проток и густината на течноста.[42]
Молекуларна физика[уреди | уреди извор]
Кај повеќе атомските молекули, движењето на молекулите може да се опише со вртењето на апсолутно тврдо тело и внатрешната вибрација на атомите околу сопствената местоположба на рамнотежа. Како резултат на вибрациите на атомите, атомите се во движење релативно на вртежниот координатен систем на молекулата. Поради овие причини ќе има појава на Кориолисовиот ефект кој ќе предизвика молекулите да се движат во насока нормална на оригиналните осцилации. Ова води кон мешање на молекуларните спектри меѓу раотациони и вибрациони нивоа од кои можат да се утврдат Кориолисовите парни постојани.[43]
Лет на инсекти[уреди | уреди извор]
Мувите (двокрилци) и молците (пеперуги) го користат Кориолисовиот ефект кога летаат: нивните трепкачи, или антените во случајот кај молците, осцилираат брзо и се користат како вибрациони жироскопи.[44] Погледај Кориолисовиот ефект од важност за стабилноста на инсектите.[45] Во сето изнесеното погоре, Кориолисовиот ефект нема ништо заедничко со вртењето на Земјата.
Поврзано[уреди | уреди извор]
- Аналитичка механика
- Применета механика
- Центрифугална сила
- Центрипетална сила
- Класична механика
- Динамика (физика)
- Земјино вртење
- Екваторски Росбиев бран
- Жироскоп
- Кинетика
- Статика
Наводи[уреди | уреди извор]
- ↑ Bhatia, V.B. (1997). Classical Mechanics: With introduction to Nonlinear Oscillations and Chaos. Narosa Publishing House. стр. 201. ISBN 81-7319-105-0.
- ↑ Graney, Christopher M. (2011). „Coriolis effect, two centuries before Coriolis“. Physics Today. 64: 8. Bibcode:2011PhT....64h...8G. doi:10.1063/PT.3.1195.
- ↑ G-G Coriolis (1835). „Sur les équations du mouvement relatif des systèmes de corps“. J. de l'Ecole royale polytechnique. 15: 144–154.
- ↑ Dugas, René and J. R. Maddox (1988). A History of Mechanics. Courier Dover Publications: p. 374. ISBN 0-486-65632-2
- ↑ Bartholomew Price (1862). A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems. Oxford : University Press. стр. 418–420.
- ↑ Arthur Gordon Webster (1912). The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies. B. G. Teubner. стр. 320. ISBN 1-113-14861-6.
- ↑ Edwin b. Wilson (1920). James McKeen Cattell (уред.). „Space, Time, and Gravitation“. The Scientific Monthly. American Association for the Advancement of Science. 10: 226.
- ↑ William Ferrel (November 1856). „An Essay on the Winds and the Currents of the Ocean“ (PDF). Nashville Journal of Medicine and Surgery. xi (4): 7–19. Архивирано од изворникот (PDF) на 2013-10-11. Посетено на 2014-07-09. Посетено на 1 January 2009.
- ↑ Anders O. Persson. „The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885“ (PDF). Архивирано од изворникот (PDF) на 2013-10-15. Посетено на 2014-07-09. Наводот journal бара
|journal=(help) - ↑ Hestenes, David (1990). New Foundations for Classical Mechanics. The Netherlands: Kluwer Academic Publishers. стр. 312. ISBN 90-277-2526-8.
- ↑ John M. Wallace and Peter V. Hobbs (1977). Atmospheric Science: An Introductory Survey. Academic Press, Inc. стр. 368–371. ISBN 0-12-732950-1.
- ↑ Sheldon M. Ebenholtz (2001). Oculomotor Systems and Perception. Cambridge University Press. ISBN 0-521-80459-0.
- ↑ George Mather (2006). Foundations of perception. Taylor & Francis. ISBN 0-86377-835-6.
- ↑ Roger Graham Barry, Richard J. Chorley (2003). Atmosphere, Weather and Climate. Routledge. стр. 113. ISBN 0-415-27171-1.
- ↑ 15,0 15,1 The claim is made that in the Falklands in WW I, the British failed to correct their sights for the southern hemisphere, and so missed their targets. John Edensor Littlewood (1953). A Mathematician's Miscellany. Methuen And Company Limited. стр. 51. John Robert Taylor (2005). Classical Mechanics. University Science Books. стр. 364; Problem 9.28. ISBN 1-891389-22-X. For set up of the calculations, seeDonald E. Carlucci, Sidney S. Jacobson (2007). Ballistics. CRC Press. стр. 225. ISBN 1-4200-6618-8.
- ↑ Lakshmi H. Kantha & Carol Anne Clayson (2000). Numerical Models of Oceans and Oceanic Processes. Academic Press. стр. 103. ISBN 0-12-434068-7.
- ↑ Stephen D. Butz (2002). Science of Earth Systems. Thomson Delmar Learning. стр. 305. ISBN 0-7668-3391-7.
- ↑ James R. Holton (2004). An Introduction to Dynamic Meteorology. Academic Press. стр. 18. ISBN 0-12-354015-1.
- ↑ Donald E. Carlucci & Sidney S. Jacobson (2007). Ballistics: Theory and Design of Guns and Ammunition. CRC Press. стр. 224–226. ISBN 1-4200-6618-8.
- ↑ William Menke & Dallas Abbott (1990). Geophysical Theory. Columbia University Press. стр. 124–126. ISBN 0-231-06792-5.
- ↑ James R. Holton (2004). An Introduction to Dynamic Meteorology. Burlington, MA: Elsevier Academic Press. стр. 64. ISBN 0-12-354015-1.
- ↑ Brinney, Amanda. „Coriolis Effect - An Overview of the Coriolis Effect“. About.com.
- ↑ Roger Graham Barry & Richard J. Chorley (2003). Atmosphere, Weather and Climate. Routledge. стр. 115. ISBN 0-415-27171-1.
- ↑ Cloud Spirals and Outflow in Tropical Storm Katrina Архивирано на 30 септември 2006 г. from Earth Observatory (NASA)
- ↑ John Marshall & R. Alan Plumb (2007). p. 98. Amsterdam: Elsevier Academic Press. ISBN 0-12-558691-4.
- ↑ Y. A. Stepanyants and G. H. Yeoh (2008). Physics: A World View. 604. Cengage Learning. стр. 77–98. ISBN 978-0-discharge Проверете ја вредноста
|isbn=: invalid character (help). Посетено на 1 April 2011. - ↑ „Stationary bathtub vortices and a critical regime of liquid fromPage=online&aid=1878300“. Journal of Fluid Mechanics. Bibcode:2008JFM...604...77S. doi:10.1017/S0022112008001080.
- ↑ Creative Media Applications (2004). A Student's Guide to Earth Science: Words and terms. Greenwood Publishing Group. стр. 22. ISBN 978-0-313-32902-9.
- ↑ Emery, C. Eugene, Jr. (May 1, 1995). "X-Files coriolis error leaves viewers wondering". Skeptical Inquirer
- ↑ Fraser, Alistair. „Bad Coriolis“. Bad Meteorology. Pennsylvania State College of Earth and Mineral Science. Посетено на 17 January 2011.
- ↑ Tipler, Paul (1998). Physics for Engineers and Scientists (4. изд.). W.H.Freeman, Worth Publishers. стр. 128. ISBN 978-1-57259-616-0.
...on a smaller scale, the coriolis effect causes water draining out a bathtub to rotate counter clockwise in the northern hemisphere...
- ↑ Tumlirz, Ottokar (1908). „Ein neuer physikalischer Beweis für die Achsendrehung der Erde“. Sitzungsberichte der math.-nat. Klasse der kaiserlichen Akademie der Wissenschaften IIa. 117: 819–841.
- ↑ Shapiro, Ascher H. (1962). „Bath-Tub Vortex“. Nature. 196 (4859): 1080. Bibcode:1962Natur.196.1080S. doi:10.1038/1961080b0.
- ↑ (Vorticity, Part 1). Web.mit.edu. Посетено на 8 November 2011.
- ↑ Тука описот „радијално навнатре“ означува „кон оската на вртење“. Оваа насока не е кон центарот на кривата на патеката, но е насоката на вистинската центрипетална сила. Па оттука и наводниците кај „центрипетална“.
- ↑ George E. Owen (2003). Fundamentals of Scientific Mathematics (original edition published by Harper & Row, New York, 1964. изд.). Courier Dover Publications. стр. 23. ISBN 0-486-42808-7.
- ↑ Morton Tavel (2002). Contemporary Physics and the Limits of Knowledge. Rutgers University Press. стр. 88. ISBN 0-8135-3077-6.
- ↑ James R Ogden & M Fogiel (1995). High School Earth Science Tutor. Research & Education Assoc. стр. 167. ISBN 0-87891-975-9.
- ↑ James Greig McCully (2006). Beyond the moon: A Conversational, Common Sense Guide to Understanding the Tides. World Scientific. стр. 74–76. ISBN 981-256-643-0.
- ↑ Кога сад со течност се врти на маса во вртење, површината на течноста природно ја зазема правилната параболичен облик. Овој факт може да се искористи за да се изработи параболична маса во вртење користејќи течност која се стврднува по неколку часови, како на пример вештачка смола. За видео на кое е прикажан Кориолисовиот ефект на ваква површина, погледај Лабраториски приказ на динамика на геофизичка течност Архивирано на 20 ноември 2005 г. John Marshall, Massachusetts Institute of Technology.
- ↑ John Marshall & R. Alan Plumb (2007). Atmosphere, Ocean, and Climate Dynamics: An Introductory Text. Academic Press. стр. 101. ISBN 0-12-558691-4.
- ↑ Omega Engineering. „Mass Flowmeters“. Наводот journal бара
|journal=(help) - ↑ califano, S (1976). Vibrational states. Wiley. стр. 226–227. ISBN 0471129968.
- ↑ "Antennae as Gyroscopes", Science, Vol. 315, 9 February 2007, p. 771
- ↑ Wu, W.C.; Wood, R.J.; Fearing, R.S. (2002). „Halteres for the micromechanical flying insect“. IEEE International Conference on Robotics and Automation, 2002. Proceedings. ICRA '02. 1: 60–65. doi:10.1109/ROBOT.2002.1013339. ISBN 0-7803-7272-7.CS1-одржување: повеќе имиња: список на автори (link)
| ||||||||||||||||||||||||||||
|
| Статијата „Кориолисова сила“ е избрана статија. Ве повикуваме и Вас да напишете и предложите избрана статија (останати избрани статии). |
















![{\displaystyle {\begin{aligned}{\boldsymbol {F_{f}}}&=-2\,m\,{\boldsymbol {\Omega \times v}}-m\,{\boldsymbol {\Omega \times {(\Omega \times r)}}}\\[8pt]&=+2\,m\,{\boldsymbol {\Omega \times (\Omega \times r)}}-m\,{\boldsymbol {\Omega \times {(\Omega \times r)}}}\\[8pt]&=m\,{\boldsymbol {\Omega \times (\Omega \times r)}}\\[8pt]&=m\,{\boldsymbol {(\Omega (\Omega \cdot r)}}-{\boldsymbol {r(\Omega \cdot \Omega ))}}\\[8pt]&=-m\,\Omega ^{2}\,{\boldsymbol {(r}}-\mid {\boldsymbol {r}}\mid \sin(\delta ){\boldsymbol {u_{\Omega })}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a996ffb4ecb3b8b5955d7af65d211f6eb1a5af1c)


























![{\displaystyle \left.{\color {white}...}\ \omega v\left(\cos \alpha +\omega t\sin \alpha \right)\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d7f3affe25ead305085872d1dcf7f0ce6ca059c)






