Плимна сила

Плимна сила или приливна сила[1] — споредна последица од силата на тежата која ги причинува плимата и осеката. Се јавува поради тоа што силата на тежата со која едно тело дејствува врз друго не е ремномерно иста насекаде по телото — поблискиот дел од телото се привлекува посилно отколку подалечните делови. Оттука се гледа дека плимната сила е диференцијална. Да го земеме гравитациското привлекување на морињата најблиску до Месечината, копното и морињата најдалеку од неа. Постои заемно привлекување помеѓу Месечината и копнениот дел од Земјата кое дејствува на нејзиното тежиште. Меѓутоа, Месечината ги привлекува посилно поблиските мориња бидејќи се течни, па така тие во мала мера се приближуваат кон неа, предизвикувајќи плима. Подалечните мориња се привлекуваат помалку. Би се очекувало привлекувањето на подалечните да предизвика осека, но бидејќи привлекувањето (забрзувањето) на копнениот дел е посилно, добиваме релативно забрзување на тие води нанадвор. Гледајќи ја Земјата во целина, забележуваме дека сета нејзина маса заемно се првлекува со онаа на Месечината, но поблиските мориња се привлечени повеќе од подалечните, што води до одвојвуање.
Во поопшта смисла во контекст на небесната механика, поимот „плимна сила“ може да се однесува на ситуација каде телото или материјалот (на пр. водата) е претежно под гравитациското влијание на друго тело (на пр. Земјата), но е подложено на растројување гравитациските ефекти на трето тело (на пр. Месечината). Во овие случаи, вознемирувачката сила се нарекува и плимна сила[2] (на пример, пореметувачката сила на Месечината): ова е разликата помеѓу силата со која третото тело дејствува врз второто и силата со кое третото тело дејствува врз првото.[3]
Објаснување[уреди | уреди извор]

Кога на телото 1 се дејствува со гравитациска сила од друго тело 2, полето може значително да се разликува меѓу страната која е насочена кон телото 2 од страната која не е насочена кон тоа тело. Сликата 2 ја прикажува диференцијалната сила на гравитацијата на сферно тело со која дејсвува другото тело. Овие т.н. плимни сили предизвикуваат напрегања кај двете тела и можно е да ги промени облиците на двете тела, а во крајни случаи, и едно од телата целосно да се распадне.[4] Рошовата граница е растојанието од планетата на кое плимните сили ќе предизвикаат објектот да се распадне поради диференцијалната сила на гравитацијата од планетата која го надминува привлекуњето на поединечните делови на тоа тело.[5] Овие напрегања нема да се случат доколку гравитациските полиња се униформни, бидејќи униформното поле предизвикува целото тело да забрзуа заедно во иста насока со ист чекор.
Ефекти на плимната сила[уреди | уреди извор]

Во случајот на бесконечно мали еластични сфери, ефектот на плимните сили е промената на обликот на телото без да им промена на зафатнината на телото. Сферата постанува елипсоид со две испакнатини, насочени кон и од другото тело. Поголемите тела наликуваат на овоид, и се благо сплескани, односно истото што им се случува на Земјините океани под дејство на Месечината. Земјата и Месечината се вртат околу заедничкиот центар на маса или барицентар, и нивното гравитациско привлекување ја обезбедува центрипеталната сила потребна за да се задржи ваквото движење. На набљудувач на Земјата, блиску до овој барицентар, ситуацијата е следна: Земјата како тело 1 дејствува гравитациски на Месечината како тело 2. Сите делови на Земјата се изложени на гравитациските сили на Месечината, со што се предизвикува водата во океаните да се прераспредели, при што се создаваат испакнатости во близина на Месечината и на страната спротивна на Месечината.[7]
Кога едно тело се врти под дејство на плимни сили, внатрешното триење ќе доведе до постепено оддавање на вртежната кинетичка енергија како топлина. Ако телото е доволно близу до главното тело, ова може да доведе до вртење во орбитата кое е плимно сврзано, како што е случајот со Земјината месечина. Плимното загревање ги создава драматичните вулкански ефекти на Јупитеровата месечина Ија. Стресовите предизвикани од плимните сили исто така предизвикуваат постојани месечни месечинотреси на Земјината месечина.
Плимните сили придонесуваат за океанските струења, кои пак ги одредуваат светските температури преку преносот на топлината до половите. Се претпоставува дека содополнителните фактори, промената на хармонискиот ритам на плимните сили може да доведе до промена на климата. Сепак, до денес не е докажана оваа поврзаност.[8]
Плимните ефекти се особено истаканти во близина на мали тела со големи маси, како што се неутронските ѕвезди или црните дупки, каде се причина за „шпагетификацијата“ на упадната материја. Плимните сили ги создаваат океанските плими и осеки, wкаде телата одговорни за појавата се Месечината и во помала мера, Сонцето. Плимните сили се исто така причина за плимното сврзување, плимното забрзување и плимното загревање.
Математичка разработка[уреди | уреди извор]

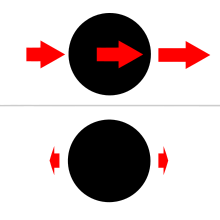
За едно (надворешно) гравитациско поле, плимното забрзување во точка во однос на телото се добива како векторска разлика од гравитациското забрзување во центарот на телото (поради надворешно создаденото поле) и гравитациското забрзување (поради истото поле) во одредена точка. Соодветно, поимот плимна сила се користи за да се опише плимното забрзување. Треба да се има предвид дека гравитациското поле кое се разгледува е само надворешното гравитациско поле, гравитациското поле на телото (како што е прикажано на графикот) не се од важност. (Со други зборови, споредбата е со услови во определена точка, како што би биле доколку нема надворешно создадено поле кое дејствува нерамномерно во определена точка во центарот на референтното тело. Надворешно создаденото поле вообичаено она создадено од движењето на трето тело, најчесто Сонцето или Месечината се најчесто употребуваните примери за точки на и над Земјината површина во геоцентричен појдовен систем.)
Плимното забрзување нем побарува постоење на вртење или тела во орбити, на пример, телото може да биде во слободен пад во права линија под влијание на гравитациското поле додека сè уште било под влијание на (променливо) плимно забрзување.
Според Њутновиот закон за сеопфатна гравитација и законите за движењето, тело со маса m на растојание R од центарот на сферта со маса M чувствува сила од ,
еднакво на забрзувањето ,
каде е единичен вектор насочен од телото M кон телото m (во овој случај забрзувањето од m кон M има негативен знак).
Да се разгледа сега забрзувањето од сефрата со маса M почувствувано од честичка до телото со маса m. при што R е растојанието од центарот на телото M до центарот на телото со маса, нека ∆r е (релативно мало) растојание на честичката од центарот на телото со маса m. Поедноставно, растојанијата првично се разгледуваат само во насока кон и од сферата со маса M. Ако телото со маса m iе сфера со полупречник ∆r, тогаш новата честичка може да се смета дека е сместена на површината, на растојание (R ± ∆r) од центарот на сферата со маса M, и за ∆r може да се земе позитивна вредност кога честичката од телото M е на растојание поголемо од R. Занемарувајќи го гравитациското забрзување кое може да биде од честичкатакон телото со маса m, може да се добие забрзувањето на честичката поради гравитациската сила кон M како:
Извлекувајќи го R2 пред заградите се добива:
Маклареновиот ред е па ќе се добие проширување:
Првиот запис е гравитациското забрзување поради масата M при центарот на референтното тело ,т.е., во точката каде е нула. Овој запис не ги опфаќа набљудуваните забрзувања на честичките на површината на m бидејќи во однос на M, m ( се што е на површината) е во слободен пад. Кога силата на подалечната честичка е одземена од силата на поблиската честичка, првиот запис се поништува, како и сите друи записи од ист ред. Останатите (остаточни) записи ја претставуваат разликата споменета погоре и се записите за плимната сила (забрзување). Кога ∆r е мало во споредба со R, записот по првиот остаточен запис е многу мал и може да се занемари, со што се добива приближното плимно забрзување (осно) при разгледувањето на растојанија како ∆r, по должина на оската која ги поврзува центрите на m и M:
- (осно)
Кога ќе се пресмета на овој начин при случајот каде ∆r е растојанието по должина на оската која ги поврзува центрите на m и M, е насочено наандвор од центарот на m (каде ∆r е нула). Плимното забрзување може да се пресмета од оската која ги поврзува телата m и M, при што е потребна векторска пресметка. Во рамнината на таа оска, плимното забрзување е насочен навнатре (кон центарот каде ∆r е нула), а големината е (осно) при линиска претоставка како на слика 2. Плимните забрзувања на површината на планетите во Сончевиот Систем воопшто се многу мали. На пример, плимното забрзување на Месечината на површината на Земјата по должина на оската Месечина-Земја е околу 1,1 × 10−7 g, додека пак сончевото плимно забрзување на површината на Земјата по должина на оската Земја-Сонце е околу 0,52 × 10−7 g, каде g е гравитациското забрзување на површината на Земјата. Па оттука нараснувачката плимна сила (забрзување) причинето од Сонцето е околу 45% од она на Месечината.[10] Сончевото плимно забрзување на површината на Земјата првпат е пресметано од страна на Њутн во неговото дело Принципи.[11]
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ Урумов, Виктор (2016). „Приливни сили“. Лексикон по физика. Скопје: Арс Ламина. стр. 122. ISBN 978-608-247-386-4.
- ↑ "On the tidal force", I N Avsiuk, in "Soviet Astronomy Letters", vol.3 (1977), pp. 96–99
- ↑ See p.509 in "Astronomy: a physical perspective", M L Kutner (2003).
- ↑ R. Penrose (1999). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. стр. 264. ISBN 0-19-286198-0.
- ↑ Thérèse Encrenaz; J -P Bibring; M Blanc (2003). The Solar System. Springer. стр. 16. ISBN 3-540-00241-3.
- ↑ R. S. MacKay; J. D. Meiss (1987). Hamiltonian Dynamical Systems: A Reprint Selection. CRC Press. стр. 36. ISBN 0-85274-205-3.
- ↑ Rollin A Harris (1920). The Encyclopedia Americana: A Library of Universal Knowledge. 26. Encyclopedia Americana Corp. стр. 611–617.
- ↑ „Millennial Climate Variability: Is There a Tidal Connection?“.
- ↑ „Inseparable galactic twins“. ESA/Hubble Picture of the Week. Посетено на 12 July 2013.
- ↑ The Admiralty (1987). Admiralty manual of navigation. 1. The Stationery Office. стр. 277. ISBN 0-11-772880-2., Chapter 11, p. 277
- ↑ Newton, Isaac (1729). The mathematical principles of natural philosophy. 2. стр. 307. ISBN 0-11-772880-2., Book 3, Proposition 36, Page 307 Newton put the force to depress the sea at places 90 degrees distant from the Sun at "1 to 38604600" (in terms of g), and wrote that the force to raise the sea along the Sun-Earth axis is "twice as great", i.e. 2 to 38604600, which comes to about 0.52 × 10−7 g as expressed in the text.
Надворешни врски[уреди | уреди извор]
- Гравитациски плими и осеки од Џ.К. Михос (англиски)
- Греј, Меган; Мерифилд, Мајкл. „Плимни сили“. Sixty Symbols. Бренди Харан за Нотингемскиот универзитет. (англиски)
- „Пау Амаро Сеоане, „Плимно пореметување на ѕвезда од масивна црна дупка"“. Архивирано од изворникот на 2017-03-13. Посетено на 2013-05-30. (англиски)
| ||||||||||||||||||||||||||||


















