Квантна механика
| Современа физика |
|---|
| Историја на современата физика |

Квантна механика — една од помладите гранки на физиката и истата се занимава со проучување на механиката во рамките на микродимензии (т.е. движење на атомски и субатомски честички), интеракции и размена на енергија помеѓу нив.
Класичната физика е неточна теорија, меѓутоа дава сосема соодветни и употребливи резултати ако се користи вон рамките на макросветот и за брзини неспоредливо помали од брзината на светлината. Ако се излезе вон рамките на класичната физика (физиката развиена од страна на Галилео Галилеј, Исак Њутн и други научници), таа дава неточни резултати и практично е бескорисна. Затоа, наместо неа се користи квантната механика (во микросветот) и релативитистичката физика (за брзини од ред на светлосната).
Важни концепти во квантната механика се:
- Дискретизација на енергијата
- Браново-честична природа на материјата
- Тунелски ефект
- Хајзенбергово начело на неопределеност
- Шредингерова равенка
- Бранова функција и нејзина интерпретација
- Приближно решавање на Шредингеровата равенка
- WBK метод
- Теорија на растројувањата
- Спин
Историја[уреди | уреди извор]
Историјата на квантната механика започнува во 1838 година со откривањето на катодните зраци од страна на Мајкл Фарадеј. По ова следувало поставувањето на проблемот на зрачење од црно тело на Густав Кирхоф, па сугестијата на Лудвиг Болцман од 1877 која вели дека енергетските состојби на физичкиот систем би можеле да се дискретни, а во 1900, Макс Планк ја објавува својата квантна хипотеза. Планковата хипотеза дека енергијата зрачи и се апсорбира во дискретни „кванти“ (или „енергетски елементи“) совршено се совпаѓала со набљудуваните закономерности на зрачењето од црно тело. Според Планк, секој енергетски елемент Е е пропорционален со неговата честота ν:
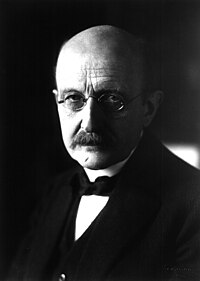
каде h e Планковата константа. Планк (внимателно) инсистирал дека ова е аспект на процесите на апсорпција и емисија на зрачењето и дека нема ништо заедничко со самата физичка реалност. Меѓутоа, во 1905 година, Алберт Ајнштајн реалистично ја протолкувал Планковата квантна хипотеза и ја искористил за да го објасни фотоелектричниот ефект, при кој светлината што зрачи на одредени материјали може да исфрли електрони од материјалот.

Основите на квантната механика биле поставени за време на првата половина од 20-от век од Макс Планк, Нилс Бор, Вернер Хајзенберг, Луј де Број, Артур Комптон, Алберт Ајнштајн, Ервин Шредингер, Макс Борн, Џон фон Нојман, Пол Дирак, Волфганг Паули, Давид Хилберт, Вилхелм Вин, Шатјендранат Бозе, Арнолд Зомерфелд и други. Во средината на 1920-тите, развојот во квантната механика довел до тоа таа да стане стандардна формулација за атомската физика. Во летото 1925, Бор и Хајзенберг објавиле резултати кои и ставиле крај на „старата квантна теорија“. И покрај партиулатното однесување во одредени процеси и мерења, светлинските кванти започнале да се нарекуваат фотони. Од ајнштајновиот едноставен постулат произлегла бура од дебати, теоретизации и тестирања. Така се појавила квантната физика, што довело до нејзино пошироко прифаќање на Петтата Солвејска конференција во 1927.
Проучувањето на електромагнетните бранови (како што е видливата светлина) исто така ја поттикнало појавата на квантната механика. Кога во 1900 Макс Планк забележа дека енергијата на брановите може да се опише како мали пакети од „кванти“, Алберт Ајнштајн ја разработи оваа идеја и покажа дека електромагнетен бран каков што е светлината може да се опише како честица (подоцна наречена фотон) со дискретен квантум на енергија која е зависна од нејзината честота. Ова доведе до теорија на единство меѓу субатомските честички и електромагнетните бранови наречена корпускуларно-бранов дуализам, според кој честичките и брановите не се ниту едното, ниту другото, туку поседуваат одредени својства на двете.
Иако квантната механика традиционално го опишувала светот на многу малото, таа исто така требала да објасни одредени скоро проучени макроскопски системи, како суперспроводниците и суперфлуидите.
Зборот квантум доаѓа од латински јазик и значи „колку големо“ или „колку многу“. Во квантната механика, тој се однесува на дискретна единица која квантната теорија ја припишува на одредени физички количества, како енергијата на атомот во невозбудена (мирна) состојба. Откритието дека честичките се дискретни пакети од енергија со брановидни својства доведе до создавање на гранката на физиката која се занимава со атомските и субатомските системи, денес наречена квантна механика. Таа е основната математичка рамка на многу полиња од физиката и хемијата, меѓу кои физика на кондензирана материја, физика на цврсто тело, атомска физика, молекуларна физика, пресметковна физика, пресметковна хемија, квантна хемија, физика на честички, јадрена хемија и јадрена физика. Некои фундаментални аспекти од оваа теорија сè уште активно се проучуваат.
Квантната механика е неопходна за разбирање на однесувањето на системите на ниво на атоми, како и на помало ниво. На пример, ако класичната механика навистина ја владеела работата на атомот, електроните брзо би се движеле кон јадрото и би се судриле со него, со што стабилните атоми би биле невозможно да постојат. Меѓутоа, во природата електроните остануваат во неодреден, недетерминистички, „разлеан“, пробабилистички орбитален пат околу (или низ) јадрото, пренебрегнувајќи го класичниот електромагнетизам.
Првобитно квантната механика била создадена да овозможи подобро објаснување на атомот, особено на разликите во спектарот на светлината емитирана од различни изотопи на еден ист елемент. Квантната теорија за атомот се развила како објаснување за останувањето на електронот во неговата орбита, што не може да се објасни со Њутновите закони за движење и Максвеловите равенки на класичниот електромагнетизам.
Во поширока смисла, квантната механика во себе вклучува четири класи на феномени кои не се предмет на проучување во класичната физика:
- Квантизација на одредени физички својства
- Корпускуларно-бранов дуализам
- Принцип на неодреденост
- Квантна разделеност.
Првата квантна теорија: Макс Планк и зрачењето од црно тело[уреди | уреди извор]

Топлинското зрачење е електромагнетно зрачење емитирано од површината на даден објект што настанува како резултат на температурата која ја поседува објектот. Ако објектот доволно се загрее, тој започнува да емитува светлина во црвениот дел на спектарот. Натамошното загревање предизвикува промена на бојата - од црвена во жолта, сина, бела - сето тоа поради емитување на светлина со сè помала бранова должина (а поголема честота). Се покажува дека совршениот емитер е и совршен апсорбер. Кога е ладно, таквиот објект изгледа совршено црн, бидејќи ја апсорбира сета светлина која паѓа на него, а не ја емитува истата. Како последица од ова, идеалниот топлински емитер е познат како црно тело, а зрачењето кое го емитува е наречено зрачење од црно тело.
Во доцниот 19 век, топлинското зрачење било релативно добро експериментално проучено. Како брановата должина на која зрачењето е најсилно се менува со температурата е дадено со Законот за Виново поместување, а целокупната моќ емитувана на единица површина е дадена со Штефан-Болцмановиот закон. Меѓутоа, класичната физика не била во можност да ја објасни врската меѓу температурата и најзастапените честоти на зрачењето. Всушност, класичната физика предвидувала дека на кратки бранови должини, енергијата бесконечно ќе се емитува од жешко тело. Овој резултат, кој е јасно дека е погрешен, е познат како ултравиолетова катастрофа. Физичарите биле во потрага по една теорија која би објаснувала зошто тие добивале вакви експериментални резултати.
Првиот модел кој можел да го објасни целосниот спектар на топлинско зрачење бил поставен од страна на Макс Планк во 1900. Тој го моделирал топлинското зрачење како да се наоѓа во рамнотежа, користејќи низа на хармониски осцилатори. За да повторно ги изведе експерименталните резултати, тој морал да претпостави дека секој осцилатор давал цел број на единици од енергија во неговата единечна карактеристична честота, а не произволно количество енергија. Со други зборови, енергијата на секој осцилатор била „квантирана“. Квантумот енергија за секој осцилатор, според Планк, бил пропорционален со честотата на осцилаторот; константата на пропорционалност денес е позната како Планкова константа. Таа обично се означува со h и има вредност 6,63⋅10-34 J s, па така енергијата E на осцилатор со честота f е дадена со
Планковиот закон бил првата квантна теорија во физиката, за што Планк ја добил Нобеловата награда во 1918 година „како признание за заслугите за напредокот на физиката со откривање на енергетските кванти“. Како и да е, во тоа време Планк сметал дека квантирањето било само математички трик, а не (како што денес е познато) фундаментална промена во нашето поимање за светот.
Фотони: квантизација на светлината[уреди | уреди извор]
Во 1905, Алберт Ајнштајн се придвижил еден чекор понапред. Тој сугерирал дека квантирањето не било само математички трик: енергијата во еден сноп светлина постои во поединечни пакети, кои сега се наречени фотони. Енергијата на еден фотон е дадена со неговата честота помножена со Планковата константа:
Со векови научниците воделе расправа за две можни теории за светлината: дали таа е бран или дали таа се состои од поток на ситни честички? Во 19 век, оваа дилема се сметала за решена во полза на брановата теорија, бидејќи можеле да се објаснат набљудуваните ефекти како рефракција, дифракција и поларизација. Џејмс Клерк Максвел покажал дека електричеството, магнетизмот и светлината се манифестации на ист феномен: електромагнетно поле. Максвеловите равенки, кои ја сочинуваат севкупната низа на закони на класичниот електромагнетизам, ја опишуваат светлината како бранови: комбинација на осцилирачки електрични и магнетни полиња. Поради предноста која ја имале доказите во полза на брановата теорија, идеите на Ајнштајн најпрво биле прифатени со голем скептицизам. Но, подоцна фотонскиот модел предничел; еден од најзначајните докази во негова полза била можноста тој да објасни неколку загадочни својства на фотоелектричниот ефект, кој е опишан во следниот пасус. Како и да е, брановата аналогија останала незаменлива при сфаќањето на другите одлики на светлината, како дифракцијата.
Фотоелектричен ефект[уреди | уреди извор]
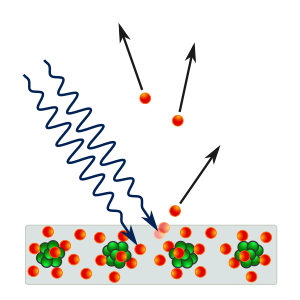
Во 1887, Хајнрих Херц забележал дека светлината може да исфрли електрони од метал. Во 1902, Филип Ленард открил дека максималната можна енергија на исфрлен електрон е поврзана со честотата на светлината, а не со нејзината јачина; ако честотата е многу мала, не се исфрлаат електрони, без разлика на јачината. Најмалата честота на светлината која предизвикува исфрлање на електроните (поттикнувачка честота) е различна за секој метал. Ова гледиште се коси со класичниот електромагнетизам, кој предвидува дека енергијата на електронот би требало да е пропорционална со јачината на зрачењето.
Ајнштајн го објаснил овој ефект постулирајќи дека сноп светлина е поток на честички (фотони), и дека ако снопот е со честота f, тогаш секој фотон има енергија еднаква на hf. Еден електрон е најверојатно да биде удрен само од еден фотон кој доделува енергија hf на електронот. Затоа, јачината на снопот нема ефект; само неговата честота ја одредува максималната енергија која може да му се додели на електронот.
За да го објасни поттикнувачкиот ефект на светлината врз исфрлањето електрони, Ајнштајн велел дека е потребна одредена количина на енергија (наречена работна функција или φ) за да се отстрани електрон од металот. Ова количество енергија е различно за секој метал. Ако енергијата на фотонот е помала од работната функција, тогаш тој не носи доволно енергија за да го отстрани (исфрли) електронот од металот. Поттикнувачката честота (f0) е честотата на фотон чија енергија е еднаква на работната функција:
Ако f е поголемо од f0, енергијата hf е доволна за да отстрани електрон. Исфрлениот електрон има кинетичка енергија EK која е (барем во повеќето случаи) еднаква на енергијата на фотонот минус енергијата потребна да се откине електронот од металот:
Описот на Ајнштајн на светлината како поток од честички ја продлабочил Планковата мисла за квантирана енергија: еден фотон со дадена честота f дава непроменлива количина енергија hf. Со други зборови, поединечните фотони можат да донесат повеќе или помалку енергија, но само во зависност од нивните честоти. Но, иако фотонот е честица, тој сè уште се опишувал како да има брановидно својство на честотата. Уште еднаш, корпускуларната природа на светлината била оспорена.
Врската меѓу честотата на електромагнетното зрачење и енергијата на секој поединечен фотон е причина зошто ултравиолетовата светлина може да предизвика изгореници на кожата, а видливата или инфрацрвената не можат. Фотон од UV светлината ќе донесе голема количина на енергија - доволна да предизвика оштетување на клетките, што е случај кај изгорениците. Фотон од инфрацрвена светлина ќе донесе помала количина на енергија - доволна само да ја загрее кожата. Така, инфрацрвена ламба може да загрее голема површина, можеби доволно голема за да им е комфорно на луѓето во ладна соба, но не може да предизвика изгореници.
Ако секој поединечен фотон би имал идентична енергија, не би било коректно да се зборува за фотон со „висока енергија“. Светлината со висока честота би можела да носи повеќе енергија само поради преплавувањето на дадена површина со повеќе фотони кои пристигнуваат за една секунда. Светлината со ниска честота би можела да носи повеќе енергија само поради истата причина. Ако беше точно дека сите фотони носат иста енергија, тогаш ако го удвоиме напливот од фотони, ние ќе го удвоиме бројот на енергетски единици кои пристигнуваат секоја секунда. Сите фотони со иста честота поседуваат иста енергија, а сите фотони со различни честоти имаат пропорционално различни енергии.
Во природата, единечните фотони ретко се среќаваат. Сонцето емитува фотони континуирано на сите електромагнетни честоти, така што изгледа дека тие се шират како непрекинат бран, а не како одделни единици. Изворите на емисија достапни на Херц и Ленард во 19 век ја имале оваа одлика. Сонце кое зрачи црвена светлина, или, пак, парче железо во леарница кое сјае со црвена боја, може да се каже дека содржат многу енергија. Би можело да се претпостави дека континуираното додавање на енергија на некое тело кое зрачи ќе направи тоа да зрачи црвена светлина, портокалова светлина, жолта светлина, зелена светлина, сина светлина, виолетова светлина итн. по редослед. Но тоа не е сосема така за големите Сонца, а поголемите парчиња железо во леарницата ќе сјаат во бои повеќе наклонети накај виолетовиот крај на спектарот. За да се промени бојата на такво тело кое зрачи, потребно е да се промени температурата, а зголемувањето на температурата ги менува квантите на енергија кои се достапни за да ги возбуди поединечните атоми до поголеми нивоа и да им овозможи да емитуваат фотони со поголеми честоти. Вкупната енергија емитувана во единица време од Сонцето или од парче железо во леарница зависи како од бројот на фотони емитувани во единица време, така и од количината енергија која ја носи секој фотон. Со други зборови, карактеристичната честота на тело кое зрачи е зависна од неговата температура. Кога физичарите гледале во снопови светлина кои содржеле голем број на поединечни и виртуелно неразлични фотони, тешко било да се разбере важноста на енергетските нивоа на поединечните фотони. Па така кога физичарите конструирале направи што го демонстрирале фотоелектричниот ефект (ефектот кој ја овозможува работата на светлинометрите на современите камери), тие најпрво очекувале дека поголема јачина светлина ќе даде поголем напон од фотоелектричната направа. Тие откриле дека јаки снопови светлина кон црвениот крај на спектарот не би произвеле електричен потанцијал, и дека слабите снопови кон виолетовиот крај на спектарот ќе дадат повисоки и повисоки волтажи. Ајнштајновата идеја дека поединечните единици светлина можат да содржат различно количество енергија во зависност од нивната честота ги објаснила експерименталните резултати кои дотогаш изгледале многу контраинтуитивни.
Квантизација на материјата: Боров модел на атомот[уреди | уреди извор]
Во раниот 20 век било познато дека атомите се состојат од дифузен облак на негативно наелектризирани електрони кои обиколуваат мало, густо и позитивно наелектризирано јадро. Ова сфаќање предложило модел во кој електроните кружат околу јадрото како планетите околу Сонцето. Меѓутоа, било исто така познато дека атомот во овој модел би бил нестабилен: според класичната теорија, електроните кои орбитираат подлежат на центростремително забрзување и притоа би требале да оддаваат електромагнетно зрачење, а загубата на енергија би причинила тие да спирализираат кон јадрото, судрувајќи се со него во дел од секундата.
Друга загатка поврзана со оваа проблематика била емисиониот спектар на атомите. Кога еден гас се загрева, тој оддава светлина само на дискретни честоти. На пример, видливата светлина оддадена од водородот се состои од четири различни бои, што е прикажано на долната слика. За споредба, белата светлина се состои од континуирана емисија долж целиот опфат на видливите честоти.

Во 1885, швајцарскиот математичар Јохан Балмер открил дека секоја бранова должина λ (ламбда) во видливиот спектар на водородот е поврзана со некој цел број n преку равенката
каде B е константа која Балмер пресметал дека е еднаква на 364.56 nm. Така, Балмеровата константа била основа за систем на дискретни, т.е. квантизирани цели броеви.
Во 1888, Јоханес Ридберг ја воопштил и ја зголемил користа на Балмеровата формула. Тој предвидел дека λ е поврзана со два цели броја n и m во она што денес е познато како Ридбергова формула:[3]
каде R е Ридбергова константа, еднаква на 0.0110 nm−1, и притоа n треба да биде поголемо од m.
Ридберговата формула се однесува на четирите видливи бранови должини на водородот со доделување вредности за m = 2 и n = 3, 4, 5, 6. Таа исто така предвидува дополнителни бранови должини во емисиониот спектар: за m = 1 и за n > 1, емисиониот спектар би требало да содржи одредени ултравиолетови бранови должини, а за m = 3 и n > 3, тој исто така би требало да содржи одредени инфрацрвени бранови должини. Експерименталното набљудување на овие бранови должини се остварило две десетлетија подоцна: во 1908 Луис Пашен открил некои од предвидените инфрацрвени бранови должини, а во 1914 Теодор Лајман открил некои од предвидените ултравиолетови бранови должини.[3]
Боров модел[уреди | уреди извор]

Во 1913, Нилс Бор предложил нов модел на атомот кој во себе ги содржел квантизираните електронски орбити.[4] Во Боровиот модел, електроните би можеле да населат само одредени орбити околу атомското јадро. Кога атомот емитувал (или апсорбирал) енергија, електронот не би се движел по континуирана траекторија од една орбита околу јадрото до друга, како што се прифаќа во класичното објаснување, туку тој инстантно би скокнал од една орбита до друга, оддавајќи ја емитуваната светлина во облик на фотон.[5] Можните енергии на фотоните оддадени од секој елемент биле одредени од разликите во енергиите меѓу орбитите, па така емисиониот спектар за секој елемент би содржел одреден број на линии.
Бор теоретизирал дека моментот на импулсот или L на даден електрон е квантизиран:
каде n е цел број, а h е Планковата константа. Поаѓајќи од оваа претпоставка, Кулоновиот закон и равенките за кружно движење покажуваат дека електрон со n единици на момент на импулс ќе кружат околу протон на растојание r дадено со
- ,
каде ke е Кулонова константа, m е масата на електронот, а e е полнежот на електронот. Поради поедноставување, ова се запишува како
каде a0, означен како Боров полупречник, е еднаков на 0.0529 nm. Боровиот полупречник е полупречникот на најмалата дозволена орбита.
Енергијата на електронот[заб. 1] може исто така да се пресмета и е дадена со
- .
Според ова, претпоставката на Бор дека моментот на импулсот е квантизиран значи дека електронот може да насели само одредени орбити околу јадрото и дека може да има само одредени енергии. Последица од овие ограничувања е дека електронот нема да се судри со јадрото: тој не може континуирано да емитува енергија, и не може да дојде поблиску до јадрото од a0 (Боровиот полупречник).
Електронот губи енергија со инстантно скокање од орбитата во која се наоѓал до пониска орбита; дополнителната енерија се емитува во облик на фотон. Спротивно, електрон кој апсорбира фотон се здобива со енергија, па затоа скока во орбита која се наоѓа подалеку од јадрото.
Секој фотон од возбудениот атомски водород потекнува од електрон што се движи од повисока орбита со полупречник rn до пониска орбита rm. Енергијата Eγ на овој фотон е разликата во енергиите En и Em на електронот:
Бидејќи Планковата равенка покажува дека енергијата на фотонот е поврзана со неговата бранова должина со изразот Eγ = hc/λ, брановите должини на светлината кои можат да се емитуваат се дадени со
Оваа равенка има ист облик како и Ридберговата формула и предвидува дека константата R би требало да биде определена со
Затоа Боровиот модел на атомот може да го предвиди емисиониот спектар на водородот во облик на фундаментални константи.[заб. 2] Меѓутоа, тој не можел да даде точни предвидувања за атомите со повеќе електрони или да објасни зошто некои спектрални линии се посветли од останатите.
Белешки[уреди | уреди извор]
- ↑ Во овој случај, енергијата на електронот е сума од неговата кинетичка и потенцијална енергија. Електронот поседува кинетичка енергија колку неговото суштинско движење околу јадрото, а потенцијална енергија поради неговото електромагнетно заемодејство со јадрото.
- ↑ Моделот лесно може да се измени за да се однесува на емисиониот спектар на секој систем што се состои од јадро и еден електрон (односно, јоните, како He+ или O7+ кои содржат само по еден електрон).
Наводи[уреди | уреди извор]
- ↑ Born, M. (1926). „Zur Quantenmechanik der Stoßvorgänge“ [On the Quantum Mechanics of Collision Processes]. Zeitschrift für Physik. 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. doi:10.1007/BF01397477. S2CID 119896026.
- ↑ Francis Weston Sears (1958). Mechanics, Wave Motion, and Heat. Addison-Wesley. стр. 537.
- ↑ 3,0 3,1 Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. стр. 147–8. ISBN 0-13-589789-0.
- ↑ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. стр. 70–89, especially p. 89. ISBN 1-84046-577-8.
- ↑ World Book Encyclopedia, page 6, 2007.
Надворешни врски[уреди | уреди извор]
- Изучување на квантната механика Архивирано на 2 септември 2013 г. на Институтот за физика при ПМФ Скопје
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|















