Корпускуларно-бранов дуализам
| Квантна механика |
|---|
Корпускуларно-бранов дуализам — својство на секоја елементарна честичка или квантен субјект да покажува својства не само на честичките, туку и на брановите. Тоа се однесува на неможноста на класичниот концепт на "честичките" или "брановите" целосно да го опише однесувањето на квантни-размери на објектите.Како што вели Ајнштајн: "Се чини дека понекогаш ние мораме да користиме една теорија, а понекогаш друга, додека пак некогаш можеме во исто време и двете да ги користиме. Се соочуваме си нов вид на тешкотии. Имаме две контрадикторни слики на реалноста; оделно ниту една од нив не го објаснува целосно феноменот на светлината, но заедно тоа го прават".[1]
Преку работата на Макс Планк, Алберт Ајнштајн, Луј де Број, Артур Комптон, Нилс Бор и многу други, моменталната научна теорија вели дека сите честички исто така имаат бранова природа (и обратно).[2] Овој феномен е потврден не само за елементарните честички, туку и за соединети честички како што се атоми или молекули. За макроскопски честички, поради нивните екстремно мали бранови должини, брановите својства неможат да бидат откриени.[3]
Иако употребата на корпускуларниот-бранов дуализам работи добро во физиката, значењето или интерпретацијата не се задоволително решени; погледни интерпретација на квантна механика.
Нилс Бор го смета "дуалниот парадокс" како основен или метафизички факт на природата. Со оглед на видот на квантните објекти ќе се покаже понегогаш бран, понекогаш честичка, карактер, во зависност на физичките опции. Тој гледа двојност како аспект на концептот на комплементарност.[4] Бор сметал дека одрекувањето од причинкиот ефект, или комплементарно од време-просторната слика од важност за квантно механичките согледувања.[5]
Вернер Хајзенберг го разгледал понатаму прашањето. Тој гледа дуалност како присуство на сите квантни субјекти, но не во вообичаената квантна механика на Бор. Тој го гледа тоа во она што се нарекува втора квантизација, која создава нов концепт на области кои постојат во обичниот простор-време. Класичните вредности на полиња ( како на пример електричното и магнетното поле предности на Максвел) се заменети со нов вид вледност на поле, како што се смета во квантна теорија за полето. Се смени мислењето дека обичната квантна механика може да биде изведена како специјализирана последица на квантната теорија за полето.[6][7]
Кратка историја за бранот и честичките[уреди | уреди извор]
Аристотел беше еден од првите што јавно дал хипотеза за природата на светлината, предлагајќи дека светлината е нарушување во елементот етер. Од друга страна Демокрит - оригиналниот атомист—тврди дека сите нешта во универзумот, вклучувајќи ја и светлината, се составени од неделиви под-компоненти.[8] На почетокот на 11 век, арапскиот научник Алхазен напишал прва сеопфатна расправа за оптика; опишувајќи рефракција, рефлексија како и работата на точкаста леќа преку светлинските зраци од точката на емисија до окото. Тој тврди дека овие зраци биле составени од светлински честички. Во 1630, Рене Декарт го популаризирал и акредитирал спротивниот опис за бранот во неговата расправа за светлината, покажувајќи дека однесувањето на светлината може да пресоздава преку моделирање на бран. Почетокот на 1670 и напредокот во текот на трите децении, Исак Њутн развива и се залагал за неговата корпускуларна хипотеза, тврдејќи дека совршените прави линии од одбивањето демонстрираат честички на светлината; само честичките можат да патуваат во такви прави линии. Тој ја објасни рефракцијата преку ставот дека честичките на светлината забрзува странично влегувајќи во погуст средина. Во исто време современиците на Њутн Роберт Хук и Кристијан Хајгенс—и подоцна Огистен-Жан Френел—математички го објаснуваат бранот, покажувајќи дека ако светлината патува со различни брзини во различни средини (како на пример вода и воздух), рефракцијата може да виде полесно објаснета како зависна од средината на ширење на бранот Хајгенс-Френелов принцип подоцна беше поддржан од Томас Јанг.[9][10] Погледите за бранот не ги менувале веднаш и погледите на зраците и честичките, но почнале да доминираат научните мисли за светлината во средината на 19 век.[11]

Џејмс Кларк Максвел открил дека може да ги комбинира четирите едноставни равенки, кои биле претходно откриени заедно со мала модификација за да го опише брановите наосцилирачките електрични и магнетни полиња. Кога била песметана брзината на ширење на електромагнетните бранови, брзина на светлината опаднала. Брзо стана јасно дека видливата светлина, ултравиолетовата светлина и инфрацрвената светлина биле електромагнетни бранови на различна честота. Теоријата на бранот преовладуваше-или барем така се чинеше.
Додека 19 век видел успех на брановата теорија во опишување на светлината, тоа исто така беше сведол на растот на атомска теорија во опишување на материјата. Антоан Лавоазје го извел законот за зачувување на масата и категоризирал многу нови хемиски елементи и соединенија; и Јозеф Луис Пруст ја унапредил хемијата со атоми покажувајќи дека елементите се комбинирани во постојани односи на маса. Ова доведе Џон Далтон да предложи дека елементите биле невидливи под-компоненти; Амедео Авогадро открил двоатомски гасови и ја довршил основната атомска теорија, дозволувајќи точните молекулски формули од најпознатите соединенија-како и точната тежина на атомот-да бидат изведени и категоризирани на доследен начин.Димитри Менделеев видел ред во периодични хемиски својства, и создал систем презентирајќи ги елементите во досега невиден ред и симетрија.
Крајот на 20 век и парадигма[уреди | уреди извор]
Честички на електрична струја[уреди | уреди извор]
На крајот од 19 век, радукционизмот на атомската теорија започнува да напредува во самиот атом; утврдувајќи ја, преку физиката, природата на атомите и хемиските реакции. Електричната струја, првин се мислело дека е течност, беше утврдено дека се состои од честички наречени електрони. Ова првпат беше демонстрирано од Џозеф Џон Томсон во 1897 година кога, користејќи катодни цевки, открил дека електричното полнж ќе патува низ вакуум. Бидејќи вакуумот не нуди средина за електичната течност да патува, ова откритие објаснува дека со помош на честичка се носи негативен полнеж и тој се движи низ вакуум. Овој електрон успешно ја третира електричната енергија како течност за многу години (што доведува до пронаоѓањето на батерии, електромотори, динамо и електролучна светлина. Уште поважно, врската меѓу електричниот полнеж и електромагнетизмот бил добро документиран следејќи ги откритијата на Мајкл Фарадеј и Џејмс Кларк Максвел. Бидејќи електромагнетизмот бил познат да биде бран генериран од страна на менување на електрични или магнетни полиња, атомскиот опис на електичната енергија и полнежот беше non sequitur. Исто така, класичната електродинамика не беше само класична теорија изречена нецелосна.
Зрачење и квантизација[уреди | уреди извор]
Во 1901 година, Макс Планк објавил анализа која успеа во повторното создавање спектар на свелина емитирана од блескав објект. За да се постигне ова, Планк требал да направи математичка претпоставка на квантизирана енергија од осцилатори (атоми од црно тело) кои емитуваат зрачење. Тоа беше Ајнштајн кој подоцна предложи дека тоа е електромагнетно зрачење кое е квантизирано.
Црнотелесно зрачење, зрачењето од електромагнетната енергија поради топлоната на објектот не може да биде објаснета само преку класичните аргументи. Теорема на рамнораспределеност од класичната механика, основа на сите класични термодинамички теореми, изјави дека енергијата на објектот е подолуна подеднакво помеѓу вибрациите на објектот мод. Но применувајќи исти причини на електромагнетното зрачење на таков топлински објект не беше толку успешно. Долго беше знаено дека терминланите објекти зрачат светлина. Бидејќи светлината беше позната да биде бранови од електромагнетизмот, физичарите се надевале да го опишат ова зрачење преку класичните закони. Ова стана познато како проблеми на црно тело. Бидејќи теоремата на рамнораспределеност работи многу добро во опишување на вибрациските модови на терминални објекти, тоа беше нормално да се претпостави дека тоа ќе се изврши подеднакво добро во опишување на радијативно зрачење на таквите објекти. Но проблемот брзо стана: ако секој мод добие еднаква поделба на енергијата, кратките модови на брановите должини ја користат енергија. Ова стана јасно кога Рејли-Џинсов закон, кога додека предвидувајчи го интензитетот на зрачења на долгите бранови должини, предиде бесконечна вкупна енергија,како што интензитетот одвојува до бесконечност за кратките бранови должини. Ова стана познато како ултравиолетова катастрофа.
Во 1900 година кога Макс Планк претпостави дека честотата на светлинското зрачење од страна на црно тело зависи од честотата на осцилатор кој зрачи и енергијата на овие осцилатори зголемува линеарно со честотата ( според неговата константа h, каде E = hν). Ова не беше несугурен предлог со оглед дека микроскопски осцилатори работат на сличен начин; кога ќе се движат пет едноставни хармонски осцилатори со еднакви амплитуди но различна честота, осцилаторите со најголема честота поседува најголема енергија. Светлика со висока честота мора да биде зрачена од осцилатор со еднаква честота и понатаму се бара дека овој осцилатор окупира повосика енергија од една помала честота, Планк избегнува какви било катастрофи, давајќи поделби на осциатори со восока честота да создаваат успешно помалку осцилатори и помало зрачење светлина.
Фотоелектричен ефект[уреди | уреди извор]
Додека Планк ја решил ултравиолетовата катастрофа со користење на атоми и квантизирани електромагнетни полиња, најсовремените физичари се согласија дека Планковиот "светлосен квант" претставува само недостатоци во неговиот модел. Во 1905 година Алберт Ајнштајн го земал Планковиот модел на црно тело за да прозиведе негово решение на друг нерешен проблен на ден; фотоелектричен ефект, каде што електроните се зрањени од атомите кога тие апсорбираат енергија од светлината.
Во 1902 година, Филип Ленард открил дека енергијата на овие исфрлени електрони не зависи од интензитетот на влезната светлина, туку од нејзината честота. Така ако еден сјае мала нискочестотна светлина врз метал, неколку ниско енергиски електрони ќе се исфрлат. Ако сега еден сјае со голем интензитет зрак на нискаочестотна светлина врз ист метал, целото мноштво од електрони ќе бидат исфрнели; тие поседуваат иста ниска енергија. Колку повеќе светлина има, повеќе електрони ќе бидат исфрлени. Каде што со цел да се добие високи енергиски електрон, еден мора да осветли метал со високочестотна светлина. Како зрачењето на црното тело, ова беше во спротивност со теоријата повикувајќи континуиран пренос на енергија помеѓу зрачењето и материјата. Ова може сè уште да биде објаснето користејќи целосно класично опишување на светлината, додека материјата е квантно механичка во природата.[12]
Ако користиме Планкова квантна енергија и побараме дека електромагнетното зрачење во дадена честота може само да пренесе енергија на материјата во цел број множители на квантната енергија hν. потоа фотоелектричниот ефект може да биде објаснет многу едноставно. Светлината на ниска честота исфрла ниски-енергиски електрони затоа што секој електрон е возбуден од апсорпцијата на еден фотон. Зголемувањето на интензитетот на светлината на нискочестотна само го сголемува бројот на возбудени електрони, не нивната енергија, затоа што енергијата на секој фотон останува ниска. Само со зголемување на честотата на светлината а со тоа и зголемување на енергијата на фотоните може еден да исфрли електрони со повисока енергија. Така, користејќи ја Планковата константа h за да се утврди енергијата на фотоните врз основа на нивната честота, енергијата на исфрлените електрони треба исто така се зголемува линеарно со честотата. Овие резултати не беа потврдени до 1915 година кога Роберт Миликан, кој претходни го има утврдено полнежот на електроните, произведе експериментални резултати во совршена согласност со предвидувањата на Ајнштајн. Додека енергијата на исфрлените електрони ја одразуваат Планковата константа, постоењето на фотоните не било експлицитно докажано до откривањето на куп на фотони ефектот, од кои современиот експеримент може да се врши во лаборатории на додипломско-ниво.[13] Овој феномен може само да биде објаснет преку фотони а не преку полукласичната теорија. Кога Ајнштајн добил своја Нобелова награда во 1921, тоа не беше за неговата тешка и математички макотрпна специјална теорија и општа релативност, туку за едноставно и тотално револуционерен предлог на квантизирана светлина.Ајнштајновите "светлински кванти" нема да бидат наречена фотони до 1925, но дури во 1905 година тие го претставиле типичниот пример за корпускуларен-бранов дуализам. Електромагнетното зрачење пропагира линеарни бранови равенки, но може да бидат испуштени или апсорбираат како дискретни елементи, па само на тој начин дејствува како бран и честичка истовремено.
Објаснувањето на Ајнштајн за фотоелектричниот ефект[уреди | уреди извор]

Во 1905 година Алберт Ајнштајн обезбедил објансување на фотоелектричниот ефект, дотогаш вознемирувачки експеримент дека брановата теорија на светлината изгледа неспособен за објаснување. Тој го стори тоа преку опишување на постоењето на фотони , кванти на светлинската енергија со квалитетни честички.
Во фотоелектричниот ефект беше забележано дека сјаејќи светлина на одредени метали ќе доведе до електрична енергија во колото. Веројатно, светлината исфрла електрони надвор од металот, со тоа што струјата тече. Како и да е, користејќи случај на калциум како пример, тоа беше исто така забележано дека додека придушеното сино светло беше доволно за да предизвика струја, дури и најсилната, светлата црвена светлина располага со технологија на време предизвикува да нема струја во целост. Според класичната теорија на светлината и материјата, силата или амплитудата на брановата светлина беше во сооднос со неговата осветленост: осветлена светлина би требало лесно да создаде голема струја. Сепак, чудно тоа не е така.
Ајнштајн го објаснува овој проблем преку аксиома дека електроните можат да добиваат енегрија од електромагнетното поле само во дискретни делови (кванти кои беа наречени фотони: износ од енергија E' која е поврзана со честотата f на светлината
каде h е Планковата константа 6.626 × 10−34 J секунди). Само фотони со доволно висока честота може да исфрли електрон слободно. На пример, фотоните на сина светлина имаат доволно енергија за да ослободат електрон од метал, но фотоните на црвена светлина неможат. Повеќе интензивната светлина над прагот на честотата може да ослободи повеќе електрони но и износот на светлина под прагот на честотата може да ослободи електрони. Да "прекрши" овој закон ќе бара екстремно ласери со висок интензитет кои сè уште не се измислени. Интензитетот-зависни феномени сега се изучуваат во детали со такви ласери.[14]
Ајнштајн бил награден за Нобеловата награда за физика во 1921 за неговото откритие на законот за фотоелектричен ефект.
Брановата должина на де Број[уреди | уреди извор]

Во 1924 година, Луј де Број формирал хипотеза на Број, тврдејќи дека сите материи [15][16] не само светлината, имаат бран-како природа;тој се однесува бранова должина (означена како λ), и импулс (означен како p):
Ова погоре е Ајнштајнова равенка, будејќи импулсот на фотонот е даден преку p = и брановатадолжина (во вакуум) преку λ = , каде c е брзина на светлината во вакуум.
Формулата на де Број беше потврдена 3 години подоцна за електрони со набљудување на дифракција на електрон во два независни експерименти. Во Универзитетот во Абердин, Џорџ Паџет Томсон донел зрак на електрон низ тенон метален филм и забележува предвидени интерференциски шеми. Во Бел Лабс Клинтон Дејвисон и Лестер Халберт Гермер упатиле нивен зрак низ кристална решетка.
Де Број беше награден со Нобеловата награда за физика во 1929 година за неговата хипотеза. Томсон и Дејвисон поделиле Нобелова награда за физика во 1937 година за нивната експериментална работа.
Принцип на неопределеност на Хајзенберг[уреди | уреди извор]
Во неговата работа на формулирање на квантна механика, Вернер Хајзенберг го постулирал неговиот принцип на неопределеност кој гласи:
каде
- тука означува стандардно отстапување,мерка на ширење или неопределеност
- x and p означуваат местоположбата на честичките и линеарниот импулс.
- претставува скратена Планкова константа (Планковата константа се дели со 2)
Хајзенберг оригинално го објаснил ова како последица од процесот на мерење: Мерењето на позицијата прецизно ќе го наруши импулсот и обратно,како на пример (гама-зрачен микроскоп) кој зависел од хипотезата на Луј де Број.За сега се мисли дека ова само делумно го објаснува феноменот,но и дека неопределноста постои и во самите честички пред некакво мерење да биде направено.
Всушност, современото објаснување на принципот на неопределеност,вклучувајќи ја и интерпрентацијата на Копенхаген првпат поставена од страна на Бор и Хајзенберг,зависи главно од природата на брановите од една честичка:Како што е безмислено да се дискутира за точната локација на бран во една низа,честичките немораат да имаат совршено точна позиција;како што е безмислено да се дискутира брановата должина на еден "пулсен" бран кој патува низ една низа,честичките немаат прецизно точен импулс ( кој одговара на инверзноста на брановата должина).Кога позицијата е релативно добро дефинирана,бранот е пулсовиден и има лошо одредена бранова должина.Кога импулсот ( така и брановата должина) се релативно добро дефинирани,бранот изгледа долг и синусоиден и тогаш има лошо дефинирана позиција.
Теоријата на Луј де Број[уреди | уреди извор]

Самиот Луј де Број предложил пилотов бран,тоа е конструкт кој го објаснува набљудуваниот Корпускуларен-бранов дуализам.Во овој поглед,секоја честичка има добро дефинирана позиција и импулс,но е водена преку брановата функција која доаѓа од Шредингеровата равенка.Пилотно-брановата теорија оригинално била одбиена бидејќи генерирала нелокални ефекти кога ќе се постават на системи кој вклучуваат повеќе од една честичка.Нелокалноста подоцна била поставена како важен дел од квантната теорија и Дејвид Бом го продолжил моделот на Број со што директно го приклучил.
Во настанатата репрезентација, која исто така се вика Де Број-Бомова теорија[18] , го објасува однесувањето на бранот како расејување со бран, затоа што движењето на честичката е предмет на водечката равенка или квантен потенцијал.[19]
Најдобра илустрација на моделот на пилотов бран е даден од експериментот "движечки капки" на Коудер во 2010 година[20] , покажувајќи го однесувањето на пилотовиот бран во макроскопски механички аналог.[17]
Брановен однос на големи објекти[уреди | уреди извор]
Уште од прикажувањата на бранововидните својства во фотоните и електроните,слични експерименти биле направено со неутрони и протони.Едни од најпознатите експерименти се експериментите на Естерман и Ото Штерн кој биле изведени во 1929.[21] Автори со слични сегашни експерименти со атоми и молекули, опишани подолу, тврдат дека овие големи честички можат да се однесуваат и како бранови.Бран наједноствано објаснето е група на честички кој се движат во одредена форма и ако го прекинеме тоа движење со некој објект ќе се претвори во зраци.
Драматични серии на експерименти кој се фокусираат на дејството на гравитацијата во однос со Корпускуларниот-бранов дуализам бил направен во 70-тите користејќи неутронов интерферометар.[22] Неутроните,како едни од главните компоненти на атомското јадро,претставуваат главна маза на јадро па така и на обичните материи.Во неутронскиот интерферометар,тие се однесуваат како квантно-механички бранови кој се под дејство на гравитација.Додека добиените резултатите не биле неочекувани бидејќи гравитацијата веќе се знаело дека се употребува секаде,вклучувајќи ја и светлината,само-интерферентноста на квантно-механичките бранови е само огромен фермион кој се наоѓа во гравитациско поле, но кое никогаш претходно не било потврдено преку експерименти.
Во 1999,дифракцијата на C60 фулерен била пријавена од страна на научниците од универзитет во Виена.[23] Фулерените се големи и масовни објекти и имаат атомска маса околу 720.Брановата должина на де Број е 2.5 пм, додека пречникот на молекулата е околу 1 нм односно 400 пати поголема. Во 2012,овие дифракциони експерименти можеле да бидат продолжени со фталоцианин молекули и негови потешки деривати,кој се составени од 58 и 114 атоми.Во овие експерименти изградбата на ваква интерференција би можела да биде снимана во вистинско време.[24][25]
Во 2003,една група од Виена ја покажа брановата природа на тетрафенилпорфирин.[26] За ова прикажување тие користеле близината на полето и Талбот Лау интерферометар.[27][28] Во самиот тој интерферометар исто така е најдена интерференција за C60F48., флуоризирана бакминстерфулерна молекула со маса од околу 1600 u,составено од 108 атоми.Големи молекули се веќе доста комплексни и даваат експериментален влез за неколку апексти на квантнен-класичен интерфејс т.е,до некое ниво и декохерентни механизми.[29][30] Во 2011,интерференција на молекулите тешка 6910 u може да биде прикана во Капица-Дирак-Талбот-Лау интерферометар.[31] Во 2013 година, била прикажана интерференцијата над 10.000 u.[32]
Дали објектите се потешки од Планковата маса и имаат де Броева бранова должина теоретски уште не се знае а и експериментално е уште недостигнато;над Планковата маса,Комптоновата бранова должина на честичката ќе биде помала од Планковата должина и ќе има свој Шварцшилдов полупречник ,големина која денешните теории од физиката ќе пробаат да ја потврдат.[33]
Неодамна Коудер, Форт покажал[34] дека ние можеме да користиме макроскопски маслени капки на вибрирачка површина како модел на корпускуларен-бранов дуализам—локализиранитр капки создаваат периодични бранови и интеракцијата со нив доведува квант-како феномен,[35] непредвидливи тунелирања[36] ,орбита квантизацијата[37] и Земанов ефект[38]
Третман во современата квантна механика[уреди | уреди извор]
Корпускуларниот-бранов дуализам е длабоко вовлечен во фондацијата на квантната механика. Во теоријата за формализам, сите информации за честичките се наоѓаат во "брановни функции",една комплексна функција која може да се гледа како аналогија на амплитудата на бран во секоја точка во вселената. Оваа функција еволвира според диференцијалната равенка (обично наречена Шредингерова равенка). За честичките со ваква маса,равенката има различни решенија кои следат различни форми на равенки за бранови.Ширењето на вакви бранови обично води до брано-виден феномен како интерференцијата и дифракцијата.Честичките без маса,како фотоните,немаат решение за Шредингеровата равенка затоа имаат уште еден бран.
Честичкото однесување е најприметливо поради феноменот кој е поврзан со мерењето во квантна механика. По завршувањето на мерењето на локацијата на честичката таа ќе биде присилена во полокализирана состојба дадена од страна на неодредениот принцип. Кога ќе биде гледано преку формализмот, ова мерење на брановата функција по случаен избор ќе се "распадне" и "одлепи". Честичките кој имаат маса шансата за наоѓање на честичката во каква било локација е еднаков на квадратна амплитуда на брановата функција. Важно е да се каже дека мерењето е само специфичен вид на интеракција кога податоците се снимаат и измерениот квантитет е присилен во одредена квантна состојба.
Следејќи го развитокот на квантната теорија за полето, недозначноста ја снемува. Полето дозволува решенија кои ја следат брановата равенка,кои обично се наречени како бранови функции.Терминот честичка е обично користен за именување на ненамаливата репрезентација на Лоренцовата група која е дозволена во полето. Интеракцијата како на пример Фејмановиот дијаграм е прифатена како добро пресметано и приближно точно каде надворешните нозе се познати како симплицирање на пропаганцијата и внатрешните линии кој се во ист ред како на зголемувањето на интеракцијата на полињата.Кога полето е нелокално и квантизирано,феномените кои претходно бил гледани како парадокси се објаснети. Во границата на корпуксуларениот-бранов дуализам, квантната теорија за полето ги дава истите резултати.
Визуализација[уреди | уреди извор]
Има повеќе начини за да се визуализира корпускуларното-браново однесување според стандардниот модел и според моделот на Број и Бом каде нема дуализам.
Подолу има илустрација на корпускуларниот-бранов дуализам кој се приближува до Де Броглиевата хипотеза и Хајзенберговиот принцип на несигурност, во однос на позицијата и импулсот на просторот, брановата функција за една честичка со маса има една димензија. Овие бранови функции се Фориеви трансформации.
Исто така колку повеќе е локализиран моментум-вселенска бранова функција,толку е повеќе шансата за честичка да биде најдена која ѓи има истите вредности на момнетум компонентите во тој регион како и помалку локализираните позициони-вселенски бранови функции со што координатите на честичката можат да биде поопширни.
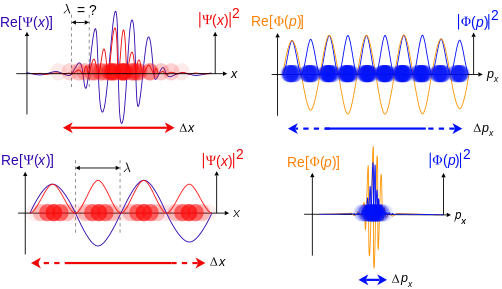
Алтернативни погледи[уреди | уреди извор]
Корпускуларниот-бранов дуализам е загатка која уште трае во мдоерната физика.Повеќето физичари ја прифаќаат теоријата како најдобро објаснување на набљудуваните феномени,но и таа не е без контроверзија.Алтернативните погледи сега ќе ги прикажеме.Овие погледи обично не се прифатени од страна на популарните физичари,но служат како основа за вредна дискусија во заедницата.
Честичниот и брановен поглед[уреди | уреди извор]
Пилотно брановиот модел, оригинално направен од Луј де Број и продолжен од страна на Дејвид Бом во теоријата за скриената варијабилност,прашува дали всушност има дуализам,дали е тоа само систем кој ги прикажува елементите на честичките и брановите истовремено и кога честичките се водени детерминизам од страна на пилитниот бран кој ќе ги насочи кон просторите со конструктивна интерференција во однос на деструктивната интерференција.Оваа идеја ја држи малцинство во заедницата на физичарите.[39]
Било кажано дека Афшаровиот експеримент[40] има можност за истовремено набљудување на брановните и честичкните елементи на фотоните.Сепак ова тврдење е одбиено од страна на други научници.
Брановен поглед[уреди | уреди извор]
Само еден научник има предложено дека дуализмот ќе може да биде заменет со само брановен поглед.Во неговата книга Collective Electrodynamics: Quantum Foundations of Electromagnetism (2000), Карвер Мид бара да се анализира однесвуањето на електроните и фотовните само во услов на електрон-брановни функции и додава на идејата на честично однесување кон квантизационите ефекти.[41]
Алберт Ајнштајн, кој во неговата потрага за теоријата за унифицираното поле, не го прифаќал корпускуларниот-брановен дуализам[42] ,верувал дека двојната природа на зрачењето била интепрентирана од страна на квантната-механика како генијално и успешна мода.
Многу светски толкувања (MWI) понекогаш се претставени само како бранова теорија, вклучувајќи го и неговиот основоположник, Хју Еверет кој наведува MWI како браново толкување.[43]
Три бранови хипотези од Р.Хородецки поврзува честичка до бран.[44][45] Хипотезата значи дека големите честички се просторни и повремено продолжени бранови фемонени од нелинеарен закон.
Честичен поглед[уреди | уреди извор]
Уште во деновите на старата квантна теорија, пред квантно-механичката верзија на корпускуларниот-брановен дуализам бил пиониран од страна на физичарот Вилијам Дуан[46] и продолжен од други вклучувајќи го Алфред Ланде[47] . Дуан ја објаснил дифракцијата на рендгенски зраци со кристал само поради нивниот честичен аспект. Девијацијата од траекторијата од различни фотони била поради квантниот моментум трансфер.[48] Фориер анализата открива дека корпускуларниот-брановен дуализам е само математички еквивалентна,постојано е тука и универзална за сите кванти. Ова сфаќање исто така може да се користи за дифракцијата на електроните од кристал.
Ниту брановен и честичен поглед[уреди | уреди извор]
Се верувало дека никогаш нема да има исти честички или бранови,само некаков компромис меѓу нив.Поради оваа причина 1928 Артур Еддингтон[49] го дефинирал поимот за ентитет кој има одлики на бранови и честички кој бил користен за опишување на предмети но не е регуларно користен денес.Едно размислување е дека 0-димензионалните математички точки неможат да бидат набљудувани. Уште едно такво размислување е формалната презентација на тие точки, Дирак-делта функцијата е нефизичка бидејќи не може да биде нормализирана.Исти аргументи можат да се употребат во чисто-бранови состојби. Роџер Пенрос вели[50] дека позиционите состојби се идејализирани брановни функции кој се спротивни во смисла на состојбите на моментумот.Додека состојбите на моментумот се бескрајно раширени,позиционите состојби се бесконечно концетрирани ни едно не може да биде нормализирано.
Релационен поглед кон корпусклуарен-бранов дуализам[уреди | уреди извор]
Односните квантни механики кој се развиваат како врска меѓу квантното поле и детекторот. Недозначноста која обично се додава кон Хајзенберговиот принцип на неопределеност и со тоа и корпускуларниот-брановен дуализам обично се избегнуваат.[51]
Апликации[уреди | уреди извор]
Иако е тешко да се нацрта одвоен корпускуларен-бранов дуализам, сепак е возможно да се набројат апликации од овие основни идеи.
- Корпускуларен-бранов дуализам се експлоатира во електронски микроскоп, каде најмалата бранова должина поврзана со електроните може да се користи за да се видат објектите многу помали отколку што се гледа користејќи видлива светлина.
- Слично на тоа неутронското расејување користи неутрони со бранова должина со околу 0.1 nm, типично растојание на цврсти атоми за да се утврди стуктурата на цврстите материи.
Наводи[уреди | уреди извор]
- ↑ Harrison, David (2002). „Complementarity and the Copenhagen Interpretation of Quantum Mechanics“. UPSCALE. Dept. of Physics, U. of Toronto. Посетено на 2008-06-21.
- ↑ Walter Greiner (2001). Quantum Mechanics: An Introduction. Springer. ISBN 3-540-67458-6.
- ↑ R. Eisberg and R. Resnick (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2. изд.). John Wiley & Sons. стр. 59–60. ISBN 047187373X.
- ↑ Kumar, Manjit (2011). Quantum: Einstein, Bohr, and the Great Debate about the Nature of Reality (Reprint. изд.). W. W. Norton & Company. стр. 242, 375–376. ISBN 978-0393339888.
- ↑ Bohr, N. (1927/1928). The quantum postulate and the recent development of atomic theory, Nature Supplement April 14 1928, 121: 580–590.
- ↑ Camilleri, K. (2009). Heisenberg and the Interpretation of Quantum Mechanics: the Physicist as Philosopher, Cambridge University Press, Cambridge UK, ISBN 978-0-521-88484-6.
- ↑ Preparata, G. (2002). An Introduction to a Realistic Quantum Physics, World Scientific, River Edge NJ, ISBN 978-981-238-176-7.
- ↑ Nathaniel Page Stites, M.A./M.S. "Light I: Particle or Wave?," Visionlearning Vol. PHY-1 (3), 2005. http://www.visionlearning.com/library/module_viewer.php?mid=132
- ↑ Young, Thomas (1804). „Bakerian Lecture: Experiments and calculations relative to physical optics“. Philosophical Transactions of the Royal Society. 94: 1–16. Bibcode:1804RSPT...94....1Y. doi:10.1098/rstl.1804.0001.
- ↑ Thomas Young: The Double Slit Experiment
- ↑ Buchwald, Jed (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. Chicago: University of Chicago Press. ISBN 0-226-07886-8. OCLC 18069573 59210058 Проверете ја вредноста
|oclc=(help). - ↑ Lamb, Willis E.; Scully, Marlan O. (1968). „The photoelectric effect without photons“ (PDF).
- ↑ „Observing the quantum behavior of light in an undergraduate laboratory“. American Journal of Physics. 72: 1210. Bibcode:2004AmJPh..72.1210T. doi:10.1119/1.1737397.
- ↑ Zhang, Q (1996). „Intensity dependence of the photoelectric effect induced by a circularly polarized laser beam“. Physics Letters A. 216 (1–5): 125–128. Bibcode:1996PhLA..216..125Z. doi:10.1016/0375-9601(96)00259-9.
- ↑ Donald H Menzel, "Fundamental formulas of Physics", volume 1, page 153; Gives the de Broglie wavelengths for composite particles such as protons and neutrons.
- ↑ Brian Greene, The Elegant Universe, page 104 "all matter has a wave-like character"
- ↑ 17,0 17,1 See this Science Channel production (Season II, Episode VI "How Does The Universe Work?"), presented by Morgan Freeman, https://www.youtube.com/watch?v=W9yWv5dqSKk
- ↑ Bohmian Mechanics, Stanford Encyclopedia of Philosophy.
- ↑ Bell, J. S., "Speakable and Unspeakable in Quantum Mechanics", Cambridge: Cambridge University Press, 1987.
- ↑ Y. Couder, A. Boudaoud, S. Protière, Julien Moukhtar, E. Fort: Walking droplets: a form of wave-particle duality at macroscopic level? , doi:10.1051/epn/2010101, (PDF)
- ↑ Estermann, I.; Stern O. (1930). „Beugung von Molekularstrahlen“. Zeitschrift für Physik. 61 (1–2): 95–125. Bibcode:1930ZPhy...61...95E. doi:10.1007/BF01340293.
- ↑ R. Colella, A. W. Overhauser and S. A. Werner, Observation of Gravitationally Induced Quantum Interference, Phys. Rev. Lett. 34, 1472–1474 (1975).
- ↑ Arndt, Markus; O. Nairz; J. Voss-Andreae, C. Keller, G. van der Zouw, A. Zeilinger (14 October 1999). „Wave–particle duality of C60“. Nature. 401 (6754): 680–682. Bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170.CS1-одржување: повеќе имиња: список на автори (link)
- ↑ Juffmann, Thomas; и др. (25 March 2012). „Real-time single-molecule imaging of quantum interference“. Nature Nanotechnology. Посетено на 27 March 2012. Наводот journal бара
|journal=(help) - ↑ Quantumnanovienna. „Single molecules in a quantum interference movie“. Посетено на 2012-04-21.
- ↑ Hackermüller, Lucia; Stefan Uttenthaler; Klaus Hornberger; Elisabeth Reiger; Björn Brezger; Anton Zeilinger; Markus Arndt (2003). „The wave nature of biomolecules and fluorofullerenes“. Phys. Rev. Lett. 91 (9): 090408. arXiv:quant-ph/0309016. Bibcode:2003PhRvL..91i0408H. doi:10.1103/PhysRevLett.91.090408. PMID 14525169.
- ↑ Clauser, John F.; S. Li (1994). „Talbot von Lau interefometry with cold slow potassium atoms“. Phys. Rev. A. 49 (4): R2213–17. Bibcode:1994PhRvA..49.2213C. doi:10.1103/PhysRevA.49.R2213. PMID 9910609. Архивирано од изворникот на 2008-08-28. Посетено на 2016-03-24.
- ↑ Brezger, Björn; Lucia Hackermüller; Stefan Uttenthaler; Julia Petschinka; Markus Arndt; Anton Zeilinger (2002). „Matter-wave interferometer for large molecules“. Phys. Rev. Lett. 88 (10): 100404. arXiv:quant-ph/0202158. Bibcode:2002PhRvL..88j0404B. doi:10.1103/PhysRevLett.88.100404. PMID 11909334. Архивирано од изворникот на 2016-05-21. Посетено на 2016-03-24.
- ↑ Hornberger, Klaus; Stefan Uttenthaler; Björn Brezger; Lucia Hackermüller; Markus Arndt; Anton Zeilinger (2003). „Observation of Collisional Decoherence in Interferometry“. Phys. Rev. Lett. 90 (16): 160401. arXiv:quant-ph/0303093. Bibcode:2003PhRvL..90p0401H. doi:10.1103/PhysRevLett.90.160401. PMID 12731960. Архивирано од изворникот на 2016-05-21. Посетено на 2016-03-24.
- ↑ Hackermüller, Lucia; Klaus Hornberger; Björn Brezger; Anton Zeilinger; Markus Arndt (2004). „Decoherence of matter waves by thermal emission of radiation“. Nature. 427 (6976): 711–714. arXiv:quant-ph/0402146. Bibcode:2004Natur.427..711H. doi:10.1038/nature02276. PMID 14973478.
- ↑ Gerlich, Stefan; и др. (2011). „Quantum interference of large organic molecules“. Nature Communications. 2 (263). Bibcode:2011NatCo...2E.263G. doi:10.1038/ncomms1263. PMC 3104521. PMID 21468015.
- ↑ Eibenberger, S.; Gerlich, S.; Arndt, M.; Mayor, M.; Tüxen, J. (2013). „Matter–wave interference of particles selected from a molecular library with masses exceeding 10 000 amu“. Physical Chemistry Chemical Physics. 15 (35): 14696–14700. doi:10.1039/c3cp51500a. PMID 23900710.
- ↑ Peter Gabriel Bergmann, The Riddle of Gravitation, Courier Dover Publications, 1993 ISBN 0-486-27378-4 online
- ↑ http://www.youtube.com/watch?v=W9yWv5dqSKk - You Tube video - Yves Couder Explains Wave/Particle Duality via Silicon Droplets
- ↑ Y. Couder, E. Fort, Single-Particle Diffraction and Interference at a Macroscopic Scale, PRL 97, 154101 (2006) online Архивирано на 21 јули 2011 г.
- ↑ A. Eddi, E. Fort, F. Moisy, Y. Couder, Unpredictable Tunneling of a Classical Wave–Particle Association, PRL 102, 240401 (2009)
- ↑ Fort, E.; Eddi, A.; Boudaoud, A.; Moukhtar, J.; Couder, Y. (2010). „Path-memory induced quantization of classical orbits“. PNAS. 107 (41): 17515–17520. doi:10.1073/pnas.1007386107.
- ↑ http://prl.aps.org/abstract/PRL/v108/i26/e264503 - Level Splitting at Macroscopic Scale
- ↑ (Buchanan pp. 29–31)
- ↑ Afshar S.S. et al: Paradox in Wave Particle Duality. Found. Phys. 37, 295 (2007) http://arxiv.org/abs/quant-ph/0702188 arXiv:quant-ph/0702188
- ↑ David Haddon. „Recovering Rational Science“. Touchstone. Посетено на 2007-09-12.
- ↑ Paul Arthur Schilpp, ed, Albert Einstein: Philosopher-Scientist, Open Court (1949), ISBN 0-87548-133-7, p 51.
- ↑ See section VI(e) of Everett's thesis: The Theory of the Universal Wave Function, in Bryce Seligman DeWitt, R. Neill Graham, eds, The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press (1973), ISBN 0-691-08131-X, pp 3–140.
- ↑ Horodecki, R. (1981). „De broglie wave and its dual wave“. Phys. Lett. A. 87 (3): 95–97. Bibcode:1981PhLA...87...95H. doi:10.1016/0375-9601(81)90571-5.
- ↑ Horodecki, R. (1983). „Superluminal singular dual wave“. Lett. Novo Cimento. 38: 509–511.
- ↑ Duane, W. (1923). The transfer in quanta of radiation momentum to matter, Proc. Natl. Acad. Sci. 9(5): 158–164.
- ↑ Landé, A. (1951). Quantum Mechanics, Sir Isaac Pitman and Sons, London, pp. 19–22.
- ↑ Heisenberg, W. (1930). The Physical Principles of the Quantum Theory, translated by C. Eckart and F.C. Hoyt, University of Chicago Press, Chicago, pp. 77–78.
- ↑ Eddington, Arthur Stanley (1928). The Nature of the Physical World. Cambridge, UK.: MacMillan. стр. 201.
- ↑ Penrose, Roger (2007). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage. стр. 521, §21.10. ISBN 978-0-679-77631-4.
- ↑ http://www.quantum-relativity.org/Quantum-Relativity.pdf Архивирано на 17 декември 2008 г.. See Q. Zheng and T. Kobayashi, Quantum Optics as a Relativistic Theory of Light; Physics Essays 9 (1996) 447. Annual Report, Department of Physics, School of Science, University of Tokyo (1992) 240.












