Бран: Разлика помеѓу преработките
| [проверена преработка] | [проверена преработка] |
поправка на правопис |
поправка на правопис |
||
| Ред 69: | Ред 69: | ||
===Замав и модулација=== |
===Замав и модулација=== |
||
[[Податотека:Wave packet.svg|мини|десно|Приказ на ''опколникот'' ( |
[[Податотека:Wave packet.svg|мини|десно|Приказ на ''опколникот'' (бавно променливата црвена крива) на замавно-модулиран бран. Брзо променливата сина крива е ''носечкиот'' бран, кој е под дејство на модулацијата.]] |
||
{{Главна статија|Модулација на замавот}} |
{{Главна статија|Модулација на замавот}} |
||
{{Поврзано|Модулација на фреквенцијата|Модулација на фазата}} |
{{Поврзано|Модулација на фреквенцијата|Модулација на фазата}} |
||
| ⚫ | Замавот на бранот може да биде постојан (и во тој случај станува збор за ''п.б.'' или ''[[постојан бран]]''), или може да биде ''модулиран'' така што ќе се менува со времето и/или местоположбата. Границата на промената на замавот се нарекува ''опколник'' на бранот. Математички, [[модулација на замавот|модулираниот бран]] може да се запише во обликот:<ref name=Jirauschek> |
||
| ⚫ | Замавот на бранот може да биде постојан (и во тој случај станува збор за ''п.б.'' или ''[[постојан бран]]''), или може да биде ''модулиран'' така што ќе се менува со времето и/или местоположбата. Границата на промената на замавот се нарекува ''опколник'' |
||
{{cite book |url = http://books.google.com/?id=6kOoT_AX2CwC&pg=PA9 |page = 9 |title = FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection |author = Christian Jirauschek |isbn = 3-86537-419-0 |year = 2005 |publisher = Cuvillier Verlag }} |
{{cite book |url = http://books.google.com/?id=6kOoT_AX2CwC&pg=PA9 |page = 9 |title = FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection |author = Christian Jirauschek |isbn = 3-86537-419-0 |year = 2005 |publisher = Cuvillier Verlag }} |
||
| Ред 99: | Ред 98: | ||
:<math>u(x,t) = A(x - v_g \ t)\sin (kx - \omega t + \phi) \ , </math> |
:<math>u(x,t) = A(x - v_g \ t)\sin (kx - \omega t + \phi) \ , </math> |
||
со што се покажува дека опколникот се движи со групната брзина и го задржува сопствениот облик. Во спротивно, во случаите каде групната брзина се менува со брановата должина, обликот на пулсот се менува на начин често опишан со |
со што се покажува дека опколникот се движи со групната брзина и го задржува сопствениот облик. Во спротивно, во случаите каде групната брзина се менува со брановата должина, обликот на пулсот се менува на начин често опишан со употреба на ''опколната равенка''.<ref name=Chen/><ref name=Recami> |
||
{{cite book |title = Localized Waves |chapter = Localization and Wannier wave packets in photonic crystals |author = Stefano Longhi, Davide Janner |editor = Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami |url = http://books.google.com/?id=xxbXgL967PwC&pg=PA329 |page = 329 |isbn = 0-470-10885-1 |year = 2008 |publisher = Wiley-Interscience }} |
{{cite book |title = Localized Waves |chapter = Localization and Wannier wave packets in photonic crystals |author = Stefano Longhi, Davide Janner |editor = Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami |url = http://books.google.com/?id=xxbXgL967PwC&pg=PA329 |page = 329 |isbn = 0-470-10885-1 |year = 2008 |publisher = Wiley-Interscience }} |
||
| Ред 111: | Ред 110: | ||
{{Главна статија|Фазна брзина|Групна брзина}} |
{{Главна статија|Фазна брзина|Групна брзина}} |
||
Постојат две брзини кои се поврзани со брановите, тоа се: [[фазна брзина|фазната брзина]] и [[групна брзина|групната брзина]]. За да се објаснат истите, потребно е да се разгледаат различни видови на бранови облици. За |
Постојат две брзини кои се поврзани со брановите, тоа се: [[фазна брзина|фазната брзина]] и [[групна брзина|групната брзина]]. За да се објаснат истите, потребно е да се разгледаат различни видови на бранови облици. За поедноставување, испитувањето се одвива во една димензија. |
||
[[Image:Wave opposite-group-phase-velocity.gif|thumb|frame|right|Прикажан е бран со групна брзина и фазна брзина кои се со спротивна насока.]] |
[[Image:Wave opposite-group-phase-velocity.gif|thumb|frame|right|Прикажан е бран со групна брзина и фазна брзина кои се со спротивна насока.]] |
||
| Ред 125: | Ред 124: | ||
</ref> |
</ref> |
||
Другиот вид на бран може да се искористи е статична структура опишана со [[утврдувач на облик|обиколник]], кој може математички |
Другиот вид на бран може да се искористи е статична структура опишана со [[утврдувач на облик|обиколник]], кој може математички да се опише на следниов начин: |
||
:<math> \psi (x,t) = \int_{-\infty} ^{\infty}\ dk_1 \ A(k_1)\ e^{i\left(k_1x - \omega t \right)} \ , </math> |
:<math> \psi (x,t) = \int_{-\infty} ^{\infty}\ dk_1 \ A(k_1)\ e^{i\left(k_1x - \omega t \right)} \ , </math> |
||
каде сега ''A(k''<sub>1</sub>'')'' (интегралот е обратната |
каде сега ''A(k''<sub>1</sub>'')'' (интегралот е обратната Фурјеова трансформација на A(k1)) и е функција која покажува остри врвови во областа на брановите вектори Δ''k'' околу точката ''k''<sub>1</sub> = ''k''. Во експоненцијалната форма гласи: |
||
:<math> A = A_o (k_1) e^ {i \alpha (k_1)} \ , </math> |
:<math> A = A_o (k_1) e^ {i \alpha (k_1)} \ , </math> |
||
| Ред 161: | Ред 160: | ||
:<math> v_g = \frac {\hbar k}{m} \ , </math> |
:<math> v_g = \frac {\hbar k}{m} \ , </math> |
||
со што брзината на определената честичка во квантната механика е и групната брзина.<ref name=Messiah/> Бидејќи групната брзина се менува преку ''k'', обликот на брановиот пакет се проширува со текот на времето, и честичката станува помалку |
со што брзината на определената честичка во квантната механика е и групната брзина.<ref name=Messiah/> Бидејќи групната брзина се менува преку ''k'', обликот на брановиот пакет се проширува со текот на времето, и честичката станува помалку просторно определена.<ref name=Fitt> |
||
{{cite book |title = Principles of quantum mechanics: as applied to chemistry and chemical physics |author = Donald D. Fitts |url = http://books.google.com/?id=8t4DiXKIvRgC&pg=PA15 |pages = 15 ''ff'' |isbn = 0-521-65841-1 |year = 1999 |publisher = Cambridge University Press }} |
{{cite book |title = Principles of quantum mechanics: as applied to chemistry and chemical physics |author = Donald D. Fitts |url = http://books.google.com/?id=8t4DiXKIvRgC&pg=PA15 |pages = 15 ''ff'' |isbn = 0-521-65841-1 |year = 1999 |publisher = Cambridge University Press }} |
||
</ref> Со други зборови, брзината на составните бранови од брановиот пакет патуваат |
</ref> Со други зборови, брзината на составните бранови од брановиот пакет патуваат со чекор кој се менува во зависност од брановата должина, па така некои се движат побрзо од останатите, и не можат да ја одржат истата [интерференција (браново движење)|интерференциска шема]] како што бранот се движи. |
||
==Синусоидални бранови== |
==Синусоидални бранови== |
||
| Ред 171: | Ред 170: | ||
[[Податотека:Simple harmonic motion animation.gif|мини|десно|Синусоидалните бранови се слични на [[едноставно хармониско движење]].]] |
[[Податотека:Simple harmonic motion animation.gif|мини|десно|Синусоидалните бранови се слични на [[едноставно хармониско движење]].]] |
||
Математички, наједноставниот бран е (просторниот) |
Математички, наједноставниот бран е (просторниот) еднодимензионален [[синусен бран]] (или ''хармониски бран'' или ''синусоида'') со замав <math>u</math> опишан од равенката: |
||
:<math>u(x,t)= A \sin (kx- \omega t + \phi) \ , </math> |
:<math>u(x,t)= A \sin (kx- \omega t + \phi) \ , </math> |
||
| Ред 215: | Ред 214: | ||
каде <math>v</math> се нарекува фазна брзина (големина на [[фазна брзина|фазната брзина]]) на бранот и <math>f</math> е фреквенцијата на бранот. |
каде <math>v</math> се нарекува фазна брзина (големина на [[фазна брзина|фазната брзина]]) на бранот и <math>f</math> е фреквенцијата на бранот. |
||
Брановата должина може да биде корисен начин дури и кога бранот не е [[периодична функција|периодичен]] во просторот. На пример, океаните |
Брановата должина може да биде корисен начин дури и кога бранот не е [[периодична функција|периодичен]] во просторот. На пример, океаните бранот кој се приближува кон брегот, бранот кој надоаѓа се движи со променлива ''локална'' бранова должина која делумно зависи од длабочината на морското дно во споредба со висината на бранот. Анализата на бранот може да се заснова на споредба на локалната бранова должина со длабочината на водата во таа положба.<ref name=Pinet2> |
||
{{cite book |title = op. cit. |author = Paul R Pinet |url = http://books.google.com/?id=6TCm8Xy-sLUC&pg=PA242 |page = 242 |isbn = 0-7637-5993-7 |year = 2009 }} |
{{cite book |title = op. cit. |author = Paul R Pinet |url = http://books.google.com/?id=6TCm8Xy-sLUC&pg=PA242 |page = 242 |isbn = 0-7637-5993-7 |year = 2009 }} |
||
| Ред 221: | Ред 220: | ||
</ref> |
</ref> |
||
Иако произволните облици ќе се движат непроменети во помалку или повеќе во линиско временски инваријантни системи, во присуство на |
Иако произволните облици ќе се движат непроменети во помалку или повеќе во линиско временски инваријантни системи, во присуство на распрскување на [[синусен бран|синусниот бран]] е единствениот облик кој ќе се придвижува непроменет за фазата и замавот, со што се олеснува анализата.<ref> |
||
{{cite book |title = Communication Systems and Techniques |author = Mischa Schwartz, William R. Bennett, and Seymour Stein |publisher = John Wiley and Sons |year = 1995 |isbn = 978-0-7803-4715-1 |page = 208 |url = http://books.google.com/?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant }} |
{{cite book |title = Communication Systems and Techniques |author = Mischa Schwartz, William R. Bennett, and Seymour Stein |publisher = John Wiley and Sons |year = 1995 |isbn = 978-0-7803-4715-1 |page = 208 |url = http://books.google.com/?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant }} |
||
| Ред 239: | Ред 238: | ||
</ref> |
</ref> |
||
Синусоидата е дефинирана за сите временски периоди и растојанија, додека при физички ситуации се среќаваме со бранови кои постојат во ограничени временски периоди и |
Синусоидата е дефинирана за сите временски периоди и растојанија, додека при физички ситуации се среќаваме со бранови кои постојат во ограничени временски периоди и ограничен простор. Може да се искористи привиден бранов облик распределен на бесконечен збир од синусоидални бранови со употреба на [[Фурјеова анализа]]. Како резултат, едноставниот случај на единствен синусоидален бран може да е применет во повеќе општи случаи.<ref name=Stein2> |
||
{{cite book |title = ''op. cit.'' |author = Seth Stein, Michael E. Wysession |page = 32 |url = http://books.google.com/?id=Kf8fyvRd280C&pg=PA32 |isbn = 0-86542-078-5 |year = 2003 }} |
{{cite book |title = ''op. cit.'' |author = Seth Stein, Michael E. Wysession |page = 32 |url = http://books.google.com/?id=Kf8fyvRd280C&pg=PA32 |isbn = 0-86542-078-5 |year = 2003 }} |
||
| Ред 263: | Ред 262: | ||
Стоен бран, исто така познат и под името ''статичен бран'', е бран кој останува во постојана позиција. Оваа појава се случува бидејќи средината се поместува во спротивна насока од бранот, или може да настане во статична средина како резултат на [[интерференција (браново движење)|интерференција]] меѓу два бранови кои патуваат во спротивни насоки. |
Стоен бран, исто така познат и под името ''статичен бран'', е бран кој останува во постојана позиција. Оваа појава се случува бидејќи средината се поместува во спротивна насока од бранот, или може да настане во статична средина како резултат на [[интерференција (браново движење)|интерференција]] меѓу два бранови кои патуваат во спротивни насоки. |
||
''Збирот'' на два спротивно насочени бранови (со ист замав и фреквенција) се создава ''стоен бран''. Стојните бранови обично настануваат кога одредена граница го попречува движењето на бранот, со што се предизвикува браново одбивање, а со тоа се воведува и спротивно насочен движечки бран. На пример кога [[виолина|виолинска]] жица е напрегната, трансверзалните бранови се движат од местото каде жицата е притисната на [[кобилица (инструмент)|кобилицата]] и затегнатоста на [[чивија (жичен инструмент)|чивија]], од каде брановите се враќаат наназад. Меѓу кобилицата и чивијата, двата |
''Збирот'' на два спротивно насочени бранови (со ист замав и фреквенција) се создава ''стоен бран''. Стојните бранови обично настануваат кога одредена граница го попречува движењето на бранот, со што се предизвикува браново одбивање, а со тоа се воведува и спротивно насочен движечки бран. На пример кога [[виолина|виолинска]] жица е напрегната, трансверзалните бранови се движат од местото каде жицата е притисната на [[кобилица (инструмент)|кобилицата]] и затегнатоста на [[чивија (жичен инструмент)|чивија]], од каде брановите се враќаат наназад. Меѓу кобилицата и чивијата, двата спротивставени бранови се во [[антифаза]] и се поништуваат, со што се добива [[јазол (физика)|јазол]]. На средината меѓу двата јазли постои [[антијазол]], каде двата спротивно насочени бранови меѓусебно максимално се ''зајакнуваат''. Не постои збирно движење на енергијата со текот на времето. |
||
<gallery> |
<gallery> |
||
Image:Standing waves on a string.gif| |
Image:Standing waves on a string.gif|Еднодимензионални стојни бранови, [[основна фрквенција|основен]] тон и првите 5 [[обертон|обертонови]]. |
||
Image:Drum vibration mode01.gif|Дводимензионален [[вибрации на кружен тапан|стоен бран на диск]], ова е основниот тон. |
Image:Drum vibration mode01.gif|Дводимензионален [[вибрации на кружен тапан|стоен бран на диск]], ова е основниот тон. |
||
Image:Drum vibration mode21.gif|[[вибрации на кружен тапан|Стоен бран на диск]] со две |
Image:Drum vibration mode21.gif|[[вибрации на кружен тапан|Стоен бран на диск]] со две јазлови линии кои минуваат низ центарот, станува збор за обертон. |
||
</gallery> |
</gallery> |
||
| Ред 280: | Ред 279: | ||
{{Главна статија|Коефициент на пропустливост|Преносна средина}} |
{{Главна статија|Коефициент на пропустливост|Преносна средина}} |
||
Брановите вообичаено се движат по прави линии низ ''[[преносна средина]]''. Ваквите средини можат да |
Брановите вообичаено се движат по прави линии низ ''[[преносна средина]]''. Ваквите средини можат да се сведат на следниве категории: |
||
* ''гранична средина'' ако се протега до одредена големина, во спротивност ''неограничена средина'' |
* ''гранична средина'' ако се протега до одредена големина, во спротивност ''неограничена средина'' |
||
| Ред 301: | Ред 300: | ||
{{Главна статија|Интерференција (браново движење)}} |
{{Главна статија|Интерференција (браново движење)}} |
||
Брановите кои се пресретнуваат и се сложуваат преку [[принцип на суперпозиција|суперпозиција]] за да создадат нов бран наречен [[интерференција (браново движење)| |
Брановите кои се пресретнуваат и се сложуваат преку [[принцип на суперпозиција|суперпозиција]] за да создадат нов бран наречен [[интерференција (браново движење)|интерференциска шема]]. Најважните интерференциски шеми се добиваат кога брановите се во [[фаза (бранови)|фаза]]. |
||
===Прекршување=== |
===Прекршување=== |
||
{{Главна статија|прекршување (физика)}} |
{{Главна статија|прекршување (физика)}} |
||
[[Податотека:Wave refraction.gif|мини|десно|Синусоидален бран кој се движи низ средина со мала бранова брзина под агол, со што се опишува намалувањето на брановата должина и |
[[Податотека:Wave refraction.gif|мини|десно|Синусоидален бран кој се движи низ средина со мала бранова брзина под агол, со што се опишува намалувањето на брановата должина и последичната промена на насоката (прекршување).]] |
||
Прекршувањето е појавата кога бранот ја менува |
Прекршувањето е појавата кога бранот ја менува сопствената брзина. Математички, со ова се означува големината на промената на [[фазна брзина|фазната брзина]]. Најчесто, прекршувањето се случува кога бранот минува од една [[преносна средина|средина]] во друга. Големината на прекршувањето на бранот низ материјалот е определена со [[показателот на прекршување|показателот на прекршувањето]] на материјалот. Насоките на упадниот и прекршениот зрак се поврзани со показателите на прекршувањето на материјалите преку [[Снелов закон|Снеловиот закон]]. |
||
===Дифракција=== |
===Дифракција=== |
||
{{главна статија|Дифракција}} |
{{главна статија|Дифракција}} |
||
Бранот пројавува дифракција кога наидува на пречка која го закривува бранот или кога истиот сè шири по преминот низ отвор. Дифракционите особености се поизразени кога |
Бранот пројавува дифракција кога наидува на пречка која го закривува бранот или кога истиот сè шири по преминот низ отвор. Дифракционите особености се поизразени кога големината на пречката или отворот се споредливи со брановата должина на бранот. |
||
===Поларизација=== |
===Поларизација=== |
||
| Ред 320: | Ред 319: | ||
[[Податотека:Circular.Polarization.Circularly.Polarized.Light Circular.Polarizer Creating.Left.Handed.Helix.View mk.svg|мини|лево]] |
[[Податотека:Circular.Polarization.Circularly.Polarized.Light Circular.Polarizer Creating.Left.Handed.Helix.View mk.svg|мини|лево]] |
||
Еден бран е поларизиран ако трепери во една насока на рамнината. Бранот може да се поларизира со употреба на |
Еден бран е поларизиран ако трепери во една насока на рамнината. Бранот може да се поларизира со употреба на поларизациски филтри. поларизацијата на трансверзалните бранови ја опишува насоката на треперењето на рамнината нормална на насоката на движењето. |
||
Лонгитудиналните бранови како што се звучните не се подложни на поларизација. За овие бранови насоката на треперењето е по должината на насоката на движењето. |
Лонгитудиналните бранови, како што се звучните, не се подложни на поларизација. За овие бранови насоката на треперењето е по должината на насоката на движењето. |
||
===Расејување=== |
===Расејување=== |
||
| Ред 330: | Ред 329: | ||
{{Main|Расејување (оптика)|Распрснување (водени бранови)}} |
{{Main|Расејување (оптика)|Распрснување (водени бранови)}} |
||
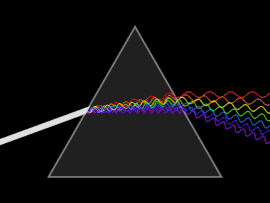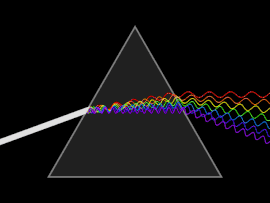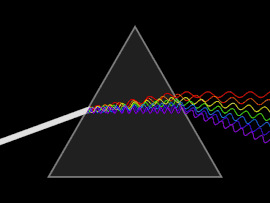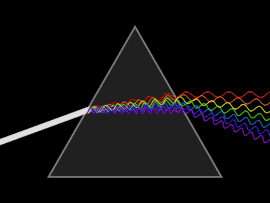
Бранот е подложен на расејување кога [[фазна брзина|фазната брзина]] или пак [[групна брзина|групната брзина]] зависи од фреквенцијата на бранот. |
|||
Расејувањето најлесно се забележува кога обична светлина се пушта да мине низ [[призма (оптика)|призма]], по што следува добивање на спектар од бои како оние на виножитото. [[Исак Њутн]] извел опити со призми и светлина и своите наоди ги запишал во ''[[Оптика]]'' од (1704 г.) и забележал дека белата светлина се состои од неколку бои и дека овие бои не можат понатамошно да се разложат.<ref name=Newton> |
Расејувањето најлесно се забележува кога обична светлина се пушта да мине низ [[призма (оптика)|призма]], по што следува добивање на спектар од бои како оние на виножитото. [[Исак Њутн]] извел опити со призми и светлина и своите наоди ги запишал во ''[[Оптика]]'' од (1704 г.) и забележал дека белата светлина се состои од неколку бои и дека овие бои не можат понатамошно да се разложат.<ref name=Newton> |
||
| Ред 366: | Ред 365: | ||
* [[браноподражавач|брановите]] на површината на барата се всушност збир од трансверзални и лонгитудинални бранови, затоа, точките на површината следат орбитална патека. |
* [[браноподражавач|брановите]] на површината на барата се всушност збир од трансверзални и лонгитудинални бранови, затоа, точките на површината следат орбитална патека. |
||
* [[Звук]]— механички бран кој се движи низ гасови, течности, |
* [[Звук]]— механички бран кој се движи низ гасови, течности, цврсти тела и плазма, |
||
* [[Инерцијални бранови]], кои се пројавуваат кај течности во кружно движење и се создадени под дејство на [[Кориолисова сила|Кориолисовата сила]]; |
* [[Инерцијални бранови]], кои се пројавуваат кај течности во кружно движење и се создадени под дејство на [[Кориолисова сила|Кориолисовата сила]]; |
||
* [[Океански површински бран|Океански површински бранови]], се движења кои се движат низ водата. |
* [[Океански површински бран|Океански површински бранови]], се движења кои се движат низ водата. |
||
| Ред 397: | Ред 396: | ||
(радио, микро, инфрацрвено, видливо и ултравиолетово) |
(радио, микро, инфрацрвено, видливо и ултравиолетово) |
||
Електромагнетниот бран се состои од два брана кои треперат во [[електрично поле|електрично]] и [[магнетно поле|магнетно]] поле. Електромагнетниот бран патува во насока |
Електромагнетниот бран се состои од два брана кои треперат во [[електрично поле|електрично]] и [[магнетно поле|магнетно]] поле. Електромагнетниот бран патува во насока која е под агол од 90 степени во однос на треперењето на двете полиња. Во {{римски|19}} век, [[Џејмс Кларк Максвел]] покажа дека, во [[вакуум]], електричното и магнетното поле се покоруваат на [[бранова равенка|брановата равенка]] со брзини еднакви на [[брзина на светлината|брзината на светлината]]. Одовде произлезе идејата дека [[видлива светлина|светлината]] е електромагнетен бран. Електромагнетните бранови можат да имаат различни фреквенции (а со тоа и бранови должини), со што се добиваат различни видови на зрачења како што се: [[радио бранови]], [[микробранови]], [[инфрацрвено зрачење|инфрацрвени]],видлива светлина, [[ултравиолетова светлина|ултравиолетови]] и [[рендгенски зраци]]. |
||
==Квантно механички бранови== |
==Квантно механички бранови== |
||
| Ред 429: | Ред 428: | ||
:<math> \mathbf{p} = \hbar \mathbf{k} \ . </math> |
:<math> \mathbf{p} = \hbar \mathbf{k} \ . </math> |
||
Но, бран како овој со определена бранова должина не е точно определена во просторот, и не може да се претстави како честичка која е определена во просторот. За да се определи точно во просторот |
Но, бран како овој со определена бранова должина не е точно определена во просторот, и не може да се претстави како честичка која е определена во просторот. За да се определи честичката точно во просторот, Деброј предложи да се постават во суперпозиција од различни бранови должини кои се со големини слични на централните бранови должини на [[бранов пакет|брановиот пакет]],<ref name=Marton> |
||
{{cite book |title = Advances in Electronics and Electron Physics |page = 271 |url = http://books.google.com/?id=g5q6tZRwUu4C&pg=PA271 |isbn = 0-12-014653-3 |year = 1980 |publisher = Academic Press |volume = 53 |editor = L. Marton & Claire Marton |author = Ming Chiang Li |chapter = Electron Interference }} |
{{cite book |title = Advances in Electronics and Electron Physics |page = 271 |url = http://books.google.com/?id=g5q6tZRwUu4C&pg=PA271 |isbn = 0-12-014653-3 |year = 1980 |publisher = Academic Press |volume = 53 |editor = L. Marton & Claire Marton |author = Ming Chiang Li |chapter = Electron Interference }} |
||
| Ред 453: | Ред 452: | ||
:<math> \psi(x,\ t=0) = A\ \exp \left( -\frac{x^2}{2\sigma^2} + i k_0 x \right) \ , </math> |
:<math> \psi(x,\ t=0) = A\ \exp \left( -\frac{x^2}{2\sigma^2} + i k_0 x \right) \ , </math> |
||
при почетно време ''t'' = 0, каде централната бранова должина е поврзана со централниот бранов вектор ''k''<sub>0</sub> и λ<sub>0</sub> = 2π / ''k''<sub>0</sub>. Сè добро познати во теоријата на [[ |
при почетно време ''t'' = 0, каде централната бранова должина е поврзана со централниот бранов вектор ''k''<sub>0</sub> и λ<sub>0</sub> = 2π / ''k''<sub>0</sub>. Сè добро познати во теоријата на [[Фурјеова анализа|Фурјеовата анализа]],<ref name=Brandt> |
||
{{cite book |page = 23 |url = http://books.google.com/?id=VM4GFlzHg34C&pg=PA23 |title = The picture book of quantum mechanics |author = Siegmund Brandt, Hans Dieter Dahmen |isbn = 0-387-95141-5 |year = 2001 |edition = 3rd |publisher = Springer }} |
{{cite book |page = 23 |url = http://books.google.com/?id=VM4GFlzHg34C&pg=PA23 |title = The picture book of quantum mechanics |author = Siegmund Brandt, Hans Dieter Dahmen |isbn = 0-387-95141-5 |year = 2001 |edition = 3rd |publisher = Springer }} |
||
</ref> или пак од [[Хајзенбергов принцип на неопределеност|Хајзенберговиот принцип на неопределеност]] (во овој случај во квантната механика) дека во мал опсег на бранови потребно е да се создаде локализиран бранов пакет, и колку што е полокализиран опколникот, толку е поголем опсегот на потребните |
</ref> или пак од [[Хајзенбергов принцип на неопределеност|Хајзенберговиот принцип на неопределеност]] (во овој случај во квантната механика) дека во мал опсег на бранови потребно е да се создаде локализиран бранов пакет, и колку што е полокализиран опколникот, толку е поголем опсегот на потребните бранови должини. [[Фурјеова трансформација|Фурјеовата трансформација]] на Гаусова функција е Гаусова функција.<ref name=Gaussian> |
||
{{cite book |title = Modern mathematical methods for physicists and engineers |author = Cyrus D. Cantrell |page = 677 |url = http://books.google.com/?id=QKsiFdOvcwsC&pg=PA677 |isbn = 0-521-59827-3 |publisher = Cambridge University Press |year = 2000 }} |
{{cite book |title = Modern mathematical methods for physicists and engineers |author = Cyrus D. Cantrell |page = 677 |url = http://books.google.com/?id=QKsiFdOvcwsC&pg=PA677 |isbn = 0-521-59827-3 |publisher = Cambridge University Press |year = 2000 }} |
||
| Ред 465: | Ред 464: | ||
:<math>f(x) = e^{-x^2 / (2\sigma^2)} \ , </math> |
:<math>f(x) = e^{-x^2 / (2\sigma^2)} \ , </math> |
||
Фурјеовата трансформација е: |
|||
:<math>\tilde{ f} (k) = \sigma e^{-\sigma^2 k^2 / 2} \ . </math> |
:<math>\tilde{ f} (k) = \sigma e^{-\sigma^2 k^2 / 2} \ . </math> |
||
Па така |
Па така Гаусовата функција во просторот се состои од бранови: |
||
:<math>f(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \ \tilde{f} (k) e^{ikx} \ dk \ ; </math> |
:<math>f(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \ \tilde{f} (k) e^{ikx} \ dk \ ; </math> |
||
| Ред 475: | Ред 474: | ||
што е всушност, број на бранови со бранови должини λ така што ''k''λ = 2 π. |
што е всушност, број на бранови со бранови должини λ така што ''k''λ = 2 π. |
||
Параметарот σ ја определува просторната распределба на Гаусовата функција по должината на ''x'' оската, додека пак |
Параметарот σ ја определува просторната распределба на Гаусовата функција по должината на ''x'' оската, додека пак Фурјеовата трансформација ја покажува распределбата на [[бранов вектор|брановиот вектор]] ''k'' определен преку 1/σ. Со други зборови, колку што е помала распределбата во просторот, толку е поголемо влијанието на ''k'', па следи дека λ = 2π/''k''. |
||
[[Податотека:GravitationalWave CrossPolarization.gif|мини|десно|Анимација која го покажува влијанието на напречно поларизираниот гравитационен бран на прстен од [[тест честичка|тест честички]]]] |
[[Податотека:GravitationalWave CrossPolarization.gif|мини|десно|Анимација која го покажува влијанието на напречно поларизираниот гравитационен бран на прстен од [[тест честичка|тест честички]]]] |
||
| Ред 483: | Ред 482: | ||
{{Главна статија|Гравитационен бран}} |
{{Главна статија|Гравитационен бран}} |
||
Научниците веруваат дека [[гравитационо зрачење|гравитационите бранови]] се движат низ просторот иако истите никогаш |
Научниците веруваат дека [[гравитационо зрачење|гравитационите бранови]] се движат низ просторот иако истите никогаш досега не биле забележани. |
||
Истите не треба да се поистоветуваат со [[тежински бран|тежинските бранови]], гравитационите бранови се нарушувања на закривеноста на [[време-простор]]от, и се предвидени од Ајнштајновата теорија за [[општа релативност|општиот релативитет]]. |
Истите не треба да се поистоветуваат со [[тежински бран|тежинските бранови]], гравитационите бранови се нарушувања на закривеноста на [[време-простор]]от, и се предвидени од Ајнштајновата теорија за [[општа релативност|општиот релативитет]]. |
||
| Ред 503: | Ред 502: | ||
* [[Фазна брзина]] |
* [[Фазна брзина]] |
||
* [[Резонанца]] |
* [[Резонанца]] |
||
* [[ |
* [[Чудовиштен бран]] |
||
* [[Стоен бран]] |
* [[Стоен бран]] |
||
== Наводи == |
== Наводи == |
||
{{наводи}} |
{{наводи}} |
||
{{commons|Бран}} |
|||
{{Гранки на физиката}} |
{{Гранки на физиката}} |
||
Преработка од 09:06, 25 октомври 2015

Бран — нарушување или треперење кое се движи низ материјата или просторот, придружено со пренос на енергија. Брановото движење ја пренесува енергијата од една точка до друга, најчесто со непостојано поместување на честичките на средината, односно без пренос на маса. Тие се состојат од треперења или вибрации околу една иста местоположба. Брановите се опишани со бранова равенка која покажува како нарушувањето се распределува со текот на времето. Математичкиот запис на оваа равенка се менува во зависност од видот на бранот.
Постојат два вида на бранови. Едните се механички бранови кои се движат низ средината, и истата таа средина се деформира. Деформацијата се поништува со помош на еластичната сила која настанува поради деформацијата. На пример, звучните бранови се движат низ молекулите на воздухот судирајќи се со нивните соседни молекули. Кога молекулите на воздухот се судираат, истовремено и отскокнуваат една од друга (еластична сила). Ова ги спречува молекулите да продолжат да се движат во насоката на бранот.
Вториот вид на бранови се електромагнетните бранови, кои за своето простирање немаат потреба од средина. Наместо тоа, тие се состојат од периодични треперења на електричното и магнетното поле, коишто пак се создадени од наелектризирани честички, и поради ова истите можат да се движат низ вакуум. Овие видови на бранови се со различни бранови должини, и според тоа тие се поделени на: радиобранови, микробранови, инфрацрвено зрачење, видлива светлина, ултравиолетова светлина, рендгенски зраци, и гама-зрачење.
Понатамошно, однесувањето на честичките во квантната механика се опишани со помош на бранови. Понатамошно, гравитационите бранови исто така патуваат низ просторот, кои се резултат на вибрација или движење на гравитационите полиња.
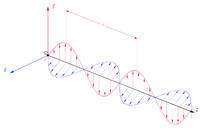
Бранот може да биде трансверзален или лонгитудинален во зависност од насоката на нивното треперење (осцилирање). Трансверзалните бранови сè добиваат кога нарушувањето создава треперења нормални на насоката на движењето. Лонгитудиналните бранови сè добиваат кога треперењата се паралелни со насоката на движење. Додека пак механичките бранови можат да бидат трансверзални и лонгитудинални, сите електромагнетни бранови се трансверзални.
Општи карактеристики
Не постои единствена, сеопфатна дефиниција за бран. Вибрацијата може да се дефинира како движење напред-назад околу одредена вредност. Како и да е, вибрацијата не е секогаш бран. Обидот да се дефинираат потребните и одредените карактеристики кои ја опишуваат појавата и истите да се наречат бран се добива неопределена граница.
Поимот бран најчесто е замислен како просторно нарушување кое не е проследено со движење на средината која го опфаќа просторот како целина. Кај бранот, енергијата на вибрацијата се оддалечува од изворот во вид на нарушување на околната средина. Како и да е, ова согледување е проблематично кај стојните бранови (на пример, браново движење на жица), каде енергијата се движи во двете насоки подеднакво, или пак за електромагнетните (на пример, светлината) бранови во вакуум, каде идејата за средина не е од корист и заемодејството со метата е клучот за забележување на бранот и практичната примена. Постојат водни бранови на површината на океаните, гама-бранови и светлински бранови оддадени од Сонцето, микробрановите кои се користат кај микробрановите печки и кај радарската опрема, радиобрановите оддадени од радио станиците и звучните бранови кои се создаваат од радио приемниците, телефонските уреди и живите суштества (преку гласовите), се само дел од брановите појави.
Може да се забележи дека описот на брановите е тесно поврзано со нивното физичко потекло за секој поединечен случај на брановиот процес. На пример, акустиката се разликува од оптиката на тој начин што звучните бранови се поврзани отколку со електромагнетните бранови чиј пренос е овозможен од вибрациите. Поимите како маса, импулс, инерција, или еластичност, се од огромно значење за опишување на акустичните (за разлика од оптичките) бранови процеси. Оваа разлика во потеклото воведува одредени бранови карактеристики карактеристични за средината низ која се простира бранот. На пример, во случајот со воздухот: вртлозите, притисокот на зрачењето, ударните бранови итн., додека пак во случајот со цврстите тела: Рејлиевите бранови, распрскувањето, и така натака.
Други карактеристики, иако опишани преку потеклото, можат да бидат важечки за сите видови на бранови. Поради овие причини, брановата теорија претставува одредена гранка од физиката која се занимава со карактеристиките на брановите процеси независно од нивното физичко потекло.[1] На пример, засновајќи се на механичкото потекло на акустичните бранови, подвижното нарушување во време-просторот постои само и само ако средината низ која се движат е бесконечно цврста или бесконечно мека. Ако сите составни делови на една средина се цврсто сврзани, тогаш сите ќе вибрираат како една целина, без задоцнување на преносот на вибрациите и поради тоа ќе отсуствува браново движење. Од друга страна, сите делови се независни, тогаш нема да има никаков пренос на вибрациите и повторно, нема да постои браново движење. Иако изнесените тврдења се безначајни во случајот со брановите кои немаат потреба од средина за да се придвижат, прикажуваат карактеристики кои се од важност за сите бранови без разлика на потеклото: кај брановите, фазата на вибрацијата е поразлична за две соседни точки во просторот бидејќи вибрацијата пристигнува до овие точки во различни временски периоди.
Слично, брановите процеси покажуваат од проучувањето на брановите дека само звучните бранови можат да се од значајност за разбирање на звучните појави. Важен пример е Јунговиот принцип за интерференција. Овој принцип беше првично претставен од Јунговото проучување на светлината и на некој начин е тема на проучување на звукот и до ден денес.
Математички опис на еднодимензионален бран
Бранови равенки
Да се замисли дека трансверзален бран (кој може да биде пулс) на жица (средина). Да се претпостави дека жицата има една просторна димензија. да се претпостави дека истиот бран се движи

- во просторната насока . Пример, нека позитивната насока биде од десната страна, а негативната насока на нека биде на лево.
- со постојан замав
- со постојана брзина , каде е
- независна од брановата должина (не е распрскувањето)
- независна од замавот (линиска средина, не е нелиниска).[2]
- со постојан бранов облик, или облик
Овој бран може да се опише со дводимензионални функции
- (бранов облик кој патува десно)
- (бранов облик кој патува лево)
или, поопшто, со помош на Даламберовата формула:[3]
каде се претставени дводелни бранови форми и кои патуваат низ средината во спротивни насоки. Општ приказ за бранот може да се добие како парцијална диференцијална равенка
Општите решенија се засновани на Диjамеловиот принцип.[4]
Бранови облици

Обликот или формата F во Даламберовата формула го вклучува записот x − vt. Постојаните вредности на записот се во согласност со постојаните вредности на F, и овие постојани вредности се добиваат ако x се зголемува за ист чекор како што се зголемува vt. Всушност, брановите имаат облик како функцијата F ќе се помести во позитивна насока x со брзина v (и G кое ќе се движи со истата брзина но во негативната насока на x).[5]
Во случај на периодична функција F со период λ, која се запишува како, F(x + λ − vt) = F(x − vt), периодичноста на F во просторот означува дека е отсликан бранот во определено време t се добива дека бранот се менува периодично во просторот со период λ (брановата должина на бранот). На сличен начин, оваа периодичност на F ја означува и периодичноста на времето: F(x − v(t + T)) = F(x − vt) преку vT = λ, па набљудувањето на бранот на статична местоположба x одредува дека бранот се движи периодично со временски период T = λ/v.[6]
Замав и модулација

Замавот на бранот може да биде постојан (и во тој случај станува збор за п.б. или постојан бран), или може да биде модулиран така што ќе се менува со времето и/или местоположбата. Границата на промената на замавот се нарекува опколник на бранот. Математички, модулираниот бран може да се запише во обликот:[7][8][9]
каде е опколникот на замавот на бранот, е брановиот број и е фазата. Ако групната брзина (погледај подолу) е браново должински независна, ова равенство може да се упрости на следниов начин:[10]
со што се покажува дека опколникот се движи со групната брзина и го задржува сопствениот облик. Во спротивно, во случаите каде групната брзина се менува со брановата должина, обликот на пулсот се менува на начин често опишан со употреба на опколната равенка.[10][11]
Фазна брзина и групна брзина

Постојат две брзини кои се поврзани со брановите, тоа се: фазната брзина и групната брзина. За да се објаснат истите, потребно е да се разгледаат различни видови на бранови облици. За поедноставување, испитувањето се одвива во една димензија.

Наједноставниот облик на бран (облик на рамнински бран) може да се изрази преку обликот:
кој може да се поврзе со обичниот синусен и косинусен облик со користење на Ојлеровата равенка. Со презапишување на обликот, , станува јасно дека со овој израз се опишува вибрацијата на брановата должина кој се движи во насока на x со постојана фазна брзина .[12]
Другиот вид на бран може да се искористи е статична структура опишана со обиколник, кој може математички да се опише на следниов начин:
каде сега A(k1) (интегралот е обратната Фурјеова трансформација на A(k1)) и е функција која покажува остри врвови во областа на брановите вектори Δk околу точката k1 = k. Во експоненцијалната форма гласи:
каде Ao е големината на A. На пример, чест избор за Ao е Гаусов бранов пакет:[13]
каде σ го определува ширењето на k1-вредности околу k, и N како ознака за замавот на бранот.
Експоненцијалната функција во интегралот за ψ трепери забрзано, ако φ(k1), и истото се променува забрзано, експоненцијалите се поништуваат, интерферираат и се поништуваат, придонесувајќи незначително кон ψ.[12] Како и да е, постои исклучок во местоположбата каде записот φ на експоненцијалот се променува помалку. (Ова набљудување е основата на овој метод на стационарна фаза за определување на овие интеграли.[14]) Условот за малата промена на φ зависи од малата промената на k1, оваа стапка на промена е:[12]
каде пресметките се направени за k1 = k бидејќи A(k1) е заснована во центарот. Овој резултат ја прикажува местоположбата на x каде фазата се менува пополека, местоположбата каде ψ е од значајност, се движи во временски период со брзина наречена групна брзина:
Групната брзина зависи од законот за распрскување кои ги поврзува ω и k. На пример, во квантната механика енергијата на честичката е претставена како бранов пакет со запис E = ħω = (ħk)2/(2m). Последично, за оваа бранова ситуација, групната брзина е:
со што брзината на определената честичка во квантната механика е и групната брзина.[12] Бидејќи групната брзина се менува преку k, обликот на брановиот пакет се проширува со текот на времето, и честичката станува помалку просторно определена.[15] Со други зборови, брзината на составните бранови од брановиот пакет патуваат со чекор кој се менува во зависност од брановата должина, па така некои се движат побрзо од останатите, и не можат да ја одржат истата [интерференција (браново движење)|интерференциска шема]] како што бранот се движи.
Синусоидални бранови

Математички, наједноставниот бран е (просторниот) еднодимензионален синусен бран (или хармониски бран или синусоида) со замав опишан од равенката:
каде
- е максималниот замав на бранот, максималното растојание од највисоката точка на нарушувањето на средината (испакнатоста) во рамнотежната точка за време на циклусот. Во приказот од десно, ова е максималното вертикално растојание меѓу основната линија и бранот.
- е просторна координата
- е временската координата
- е брановиот број
- е аголната фреквенција
- е фазна постојана.
Единицата за замавот зависи од видот на бранот. Трансверзалните механички бранови (пример, бран по жица) има замав кој се изразува како растојание (пример, метри), лонгитудиналните механички бранови (пример, звучни бранови) користат единица за притисок (пример, паскали), и електромагнетни бранови (вид на трансверзални бранови во вакуум) го изразуваат замавот преку сопственото електрично поле (пример, волти/метар).
брановата должина е растојанието меѓу две последователни испакнатини или вдлабнатини (или други исти точки), најчесто мерени во метри. Брановиот број , просторната фреквенција на бранот во радијани по единица растојание (најчесто во метри), може да се поврзе со брановата должина со записот:
Периодот е времето потребно за да се заврши еден циклус на треперењето на бранот.Фреквенцијата е бројот на периоди во единица време (во секунда) и се мери најчесто во херци. Тие се поврзани преку:
со други зборови, фреквенцијата и периодот се заемно реципрочни.
аголната фреквенција ја претставува фреквенцијата во радијани во секунда. Поврзана е со фреквенцијата или периодот преку :
Брановата должина на синусоидалниот бранов облик кој патува со постојана брзина определена со :[16]
каде се нарекува фазна брзина (големина на фазната брзина) на бранот и е фреквенцијата на бранот.
Брановата должина може да биде корисен начин дури и кога бранот не е периодичен во просторот. На пример, океаните бранот кој се приближува кон брегот, бранот кој надоаѓа се движи со променлива локална бранова должина која делумно зависи од длабочината на морското дно во споредба со висината на бранот. Анализата на бранот може да се заснова на споредба на локалната бранова должина со длабочината на водата во таа положба.[17]
Иако произволните облици ќе се движат непроменети во помалку или повеќе во линиско временски инваријантни системи, во присуство на распрскување на синусниот бран е единствениот облик кој ќе се придвижува непроменет за фазата и замавот, со што се олеснува анализата.[18] Поради Крамерс-Кронинговите соодноси, линиската средина со распрскување исто така има загуби, па синусниот бран кој се движи во распрскувачка средина е ослабен за одредени фреквенции кои зависат од самата средина.[19]
Синусната функција е периодична, па синусниот бран или синусоида со бранова должина во просторот и период во времето.[20][21]
Синусоидата е дефинирана за сите временски периоди и растојанија, додека при физички ситуации се среќаваме со бранови кои постојат во ограничени временски периоди и ограничен простор. Може да се искористи привиден бранов облик распределен на бесконечен збир од синусоидални бранови со употреба на Фурјеова анализа. Како резултат, едноставниот случај на единствен синусоидален бран може да е применет во повеќе општи случаи.[22][23] Многу од средините се линиски, или приближно линиски, па пресметката на однесувањето на привидниот бран може да се определи со додавање на резултатите на поединечните синусоидални бранови со употреба на принципот на суперпозиција за да се најде решението на општиот бранов облик.[24] Кога средината е нелиниска, решението за сложените бранови не може да се определи со разложување на синусен бран.
Рамнински бранови
Стојни бранови

Стоен бран, исто така познат и под името статичен бран, е бран кој останува во постојана позиција. Оваа појава се случува бидејќи средината се поместува во спротивна насока од бранот, или може да настане во статична средина како резултат на интерференција меѓу два бранови кои патуваат во спротивни насоки.
Збирот на два спротивно насочени бранови (со ист замав и фреквенција) се создава стоен бран. Стојните бранови обично настануваат кога одредена граница го попречува движењето на бранот, со што се предизвикува браново одбивање, а со тоа се воведува и спротивно насочен движечки бран. На пример кога виолинска жица е напрегната, трансверзалните бранови се движат од местото каде жицата е притисната на кобилицата и затегнатоста на чивија, од каде брановите се враќаат наназад. Меѓу кобилицата и чивијата, двата спротивставени бранови се во антифаза и се поништуваат, со што се добива јазол. На средината меѓу двата јазли постои антијазол, каде двата спротивно насочени бранови меѓусебно максимално се зајакнуваат. Не постои збирно движење на енергијата со текот на времето.
-
Еднодимензионални стојни бранови, основен тон и првите 5 обертонови.
-
Дводимензионален стоен бран на диск, ова е основниот тон.
-
Стоен бран на диск со две јазлови линии кои минуваат низ центарот, станува збор за обертон.
Физички особености

Брановите најчесто се под влијание на бројни ситуации, како на пример:
Пренос и средина
Брановите вообичаено се движат по прави линии низ преносна средина. Ваквите средини можат да се сведат на следниве категории:
- гранична средина ако се протега до одредена големина, во спротивност неограничена средина
- линиска средина ако замавот на различни бранови во една одредена точка може да се додаде во средината.
- еднообразна средина или хомогена средина ако особеностите не се менуваат во различни местоположби во средината.
- анизотропна средина ако една или повеќе од физичките особености се менуваат во повеќе насоки
- изотропна средина ако физиките особености се исти во сите насоки
Впивање
Преку впивањето на брановите се означува, кога одреден вид на бран ќе се судри со материја, и ќе биде впиен од таа материја. Кога бран со иста природна фреквенција наиде на атом, тогаш електроните на тој атом ќе започнат да вибрираат. Ако бран со определена фреквенција се судри со материјал кои ги има истите вибрациони фреквенции, тогаш тие електрони ќе ја впијат енергијата од бранот и истата ќе ја претворат во вибрационо движење.
Одбивање
Кога бран ќе се судри со одбивна површина, ја менува својата насока, на тој начин што аголот создаден од упадниот зрак и линијата нормална на површината е еднаков со аголот на одбиениот зрак и истата нормала.
Интерференција
Брановите кои се пресретнуваат и се сложуваат преку суперпозиција за да создадат нов бран наречен интерференциска шема. Најважните интерференциски шеми се добиваат кога брановите се во фаза.
Прекршување

Прекршувањето е појавата кога бранот ја менува сопствената брзина. Математички, со ова се означува големината на промената на фазната брзина. Најчесто, прекршувањето се случува кога бранот минува од една средина во друга. Големината на прекршувањето на бранот низ материјалот е определена со показателот на прекршувањето на материјалот. Насоките на упадниот и прекршениот зрак се поврзани со показателите на прекршувањето на материјалите преку Снеловиот закон.
Дифракција
Бранот пројавува дифракција кога наидува на пречка која го закривува бранот или кога истиот сè шири по преминот низ отвор. Дифракционите особености се поизразени кога големината на пречката или отворот се споредливи со брановата должина на бранот.
Поларизација

Еден бран е поларизиран ако трепери во една насока на рамнината. Бранот може да се поларизира со употреба на поларизациски филтри. поларизацијата на трансверзалните бранови ја опишува насоката на треперењето на рамнината нормална на насоката на движењето.
Лонгитудиналните бранови, како што се звучните, не се подложни на поларизација. За овие бранови насоката на треперењето е по должината на насоката на движењето.
Расејување
Бранот е подложен на расејување кога фазната брзина или пак групната брзина зависи од фреквенцијата на бранот. Расејувањето најлесно се забележува кога обична светлина се пушта да мине низ призма, по што следува добивање на спектар од бои како оние на виножитото. Исак Њутн извел опити со призми и светлина и своите наоди ги запишал во Оптика од (1704 г.) и забележал дека белата светлина се состои од неколку бои и дека овие бои не можат понатамошно да се разложат.[25]
Механички бранови
Бранови по жица
Брзината на трансверзалните бранови кои се движат долж жица што вибрира ( v ) е директно пропорционална на квадратниот корен на [[напор (механика)|напорот] на жицата ( T ) низ линиската густина ( μ ):
каде линиската густина μ е масата по единица должина на жицата.
Звучни бранови
Звучните или акустични бранови се движат со брзина определена со:
или квадратниот корен од адијабатскиот збирен модул поделен со моменталната густина на течноста (погледај брзина на звук).
Водни бранови

- брановите на површината на барата се всушност збир од трансверзални и лонгитудинални бранови, затоа, точките на површината следат орбитална патека.
- Звук— механички бран кој се движи низ гасови, течности, цврсти тела и плазма,
- Инерцијални бранови, кои се пројавуваат кај течности во кружно движење и се создадени под дејство на Кориолисовата сила;
- Океански површински бранови, се движења кои се движат низ водата.
Сеизмички бранови
Надзвучни бранови

Останати
- Сообраќајни бранови, поточно, движењето и густината на моторните возила, кои се моделирани како кинематички бранови.[26]
- Метахрони бранови се бранови кои се настанати под дејство на сообразни едно по други движења.
- Важно е да се напомене и равенката за еднаквоста на масата и енергијата може да се реши преку оваа форма: .
Електромагнетни бранови
(радио, микро, инфрацрвено, видливо и ултравиолетово)
Електромагнетниот бран се состои од два брана кои треперат во електрично и магнетно поле. Електромагнетниот бран патува во насока која е под агол од 90 степени во однос на треперењето на двете полиња. Во XIX век, Џејмс Кларк Максвел покажа дека, во вакуум, електричното и магнетното поле се покоруваат на брановата равенка со брзини еднакви на брзината на светлината. Одовде произлезе идејата дека светлината е електромагнетен бран. Електромагнетните бранови можат да имаат различни фреквенции (а со тоа и бранови должини), со што се добиваат различни видови на зрачења како што се: радио бранови, микробранови, инфрацрвени,видлива светлина, ултравиолетови и рендгенски зраци.
Квантно механички бранови
Шредингеровата равенка го опишува брановото однесување на честичките во квантната механика. Решенијата на оваа равенка се бранови функции со кои може да се опише густината на веројатноста за определена честичка.

Дебројеви бранови
Луј де Број го воспостави мислењето дека сите честички со импулс поседуваат бранова должина.
каде h е Планковата постојана, и p е големината на импулсот на честичката. Оваа претпоставка беше основата на квантната механика. Денеска, оваа бранова должина се нарекува Дебројева бранова должина. На пример, електроните во CRT екраните поседуваат Дебројева бранова должина од околу 10−13 m.
Бран кој ги претставува овие честички кои се движат во k-насока се изразуваат со следната бранова функција:
каде брановата должина е определена преку брановиот вектор k на следниот начин:
импулсот е определен од:
Но, бран како овој со определена бранова должина не е точно определена во просторот, и не може да се претстави како честичка која е определена во просторот. За да се определи честичката точно во просторот, Деброј предложи да се постават во суперпозиција од различни бранови должини кои се со големини слични на централните бранови должини на брановиот пакет,[28] брановиот облик кој често се користи во квантната механика за да се опише брановата функција на честичката. Кај брановиот пакет, брановата должина на честичката не е точно определена, и локалната бранова должина се движи со вредноста близу до вредноста на главната бранова должина.
При претставувањето на брановата функција на локализирана честичка, брановиот пакет често се смета дека поседува Гаусов облик кој се нарекува Гаусов бранов пакет.[29] Гаусовите бранови пакети често се користат при анализата на водните бранови.[30]
На пример, Гаусовата бранова функција ψ може да го добие следниов облик:[31]
при почетно време t = 0, каде централната бранова должина е поврзана со централниот бранов вектор k0 и λ0 = 2π / k0. Сè добро познати во теоријата на Фурјеовата анализа,[32] или пак од Хајзенберговиот принцип на неопределеност (во овој случај во квантната механика) дека во мал опсег на бранови потребно е да се создаде локализиран бранов пакет, и колку што е полокализиран опколникот, толку е поголем опсегот на потребните бранови должини. Фурјеовата трансформација на Гаусова функција е Гаусова функција.[33] Со определена Гаусова функција:
Фурјеовата трансформација е:
Па така Гаусовата функција во просторот се состои од бранови:
што е всушност, број на бранови со бранови должини λ така што kλ = 2 π.
Параметарот σ ја определува просторната распределба на Гаусовата функција по должината на x оската, додека пак Фурјеовата трансформација ја покажува распределбата на брановиот вектор k определен преку 1/σ. Со други зборови, колку што е помала распределбата во просторот, толку е поголемо влијанието на k, па следи дека λ = 2π/k.

Гравитациони бранови
Научниците веруваат дека гравитационите бранови се движат низ просторот иако истите никогаш досега не биле забележани. Истите не треба да се поистоветуваат со тежинските бранови, гравитационите бранови се нарушувања на закривеноста на време-просторот, и се предвидени од Ајнштајновата теорија за општиот релативитет.
WKB метод
Во нееднообразна средина, во која брановиот број k може да зависи како од местоположбата така и од фреквенцијата, фазниот поим kx се заменува со интегралот на k(x)dx, според WKB методот. Ваквите нееднообразни подвижни бранови се често присутни во многу физички проблеми, како што е и механиката кај полжавот во увото и брановите кај јажиња кои висат.
Поврзано
- Мексикански бран
- Биење
- Капиларни бранови
- Киматика
- Доплеров ефект
- Групна брзина
- Хармониски
- Инерцијален бран
- Фазна брзина
- Резонанца
- Чудовиштен бран
- Стоен бран
Наводи
- ↑ Lev A. Ostrovsky & Alexander I. Potapov (2002). Modulated waves: theory and application. Johns Hopkins University Press. ISBN 0-8018-7325-8.
- ↑ Michael A. Slawinski (2003). „Wave equations“. Seismic waves and rays in elastic media. Elsevier. стр. 131 ff. ISBN 0-08-043930-6.
- ↑ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975. изд.). Dover. стр. 13–14. ISBN 978-0-486-66745-4.
- ↑ Jalal M. Ihsan Shatah, Michael Struwe (2000). „The linear wave equation“. Geometric wave equations. American Mathematical Society Bookstore. стр. 37 ff. ISBN 0-8218-2749-9.
- ↑ Louis Lyons (1998). All you wanted to know about mathematics but were afraid to ask. Cambridge University Press. стр. 128 ff. ISBN 0-521-43601-X.
- ↑ Alexander McPherson (2009). „Waves and their properties“. Introduction to Macromolecular Crystallography (2. изд.). Wiley. стр. 77. ISBN 0-470-18590-2.
- ↑ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. стр. 9. ISBN 3-86537-419-0.
- ↑ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. стр. 365. ISBN 3-540-62001-X.
- ↑ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. стр. 33. ISBN 0-521-63134-3.
- ↑ 10,0 10,1 Chin-Lin Chen (2006). „§13.7.3 Pulse envelope in nondispersive media“. Foundations for guided-wave optics. Wiley. стр. 363. ISBN 0-471-75687-3.
- ↑ Stefano Longhi, Davide Janner (2008). „Localization and Wannier wave packets in photonic crystals“. Во Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami (уред.). Localized Waves. Wiley-Interscience. стр. 329. ISBN 0-470-10885-1.CS1-одржување: повеќе имиња: список на уредници (link)
- ↑ 12,0 12,1 12,2 12,3 Albert Messiah (1999). Quantum Mechanics (Reprint of two-volume Wiley 1958. изд.). Courier Dover. стр. 50–52. ISBN 978-0-486-40924-5.
- ↑ See, for example, Eq. 2(a) in Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics: An introduction (2nd. изд.). Springer. стр. 60–61. ISBN 3-540-67458-6.
- ↑ John W. Negele, Henri Orland (1998). Quantum many-particle systems (Reprint in Advanced Book Classics. изд.). Westview Press. стр. 121. ISBN 0-7382-0052-2.
- ↑ Donald D. Fitts (1999). Principles of quantum mechanics: as applied to chemistry and chemical physics. Cambridge University Press. стр. 15 ff. ISBN 0-521-65841-1.
- ↑ David C. Cassidy, Gerald James Holton, Floyd James Rutherford (2002). Understanding physics. Birkhäuser. стр. 339 ff. ISBN 0-387-98756-8.CS1-одржување: повеќе имиња: список на автори (link)
- ↑ Paul R Pinet (2009). op. cit. стр. 242. ISBN 0-7637-5993-7.
- ↑ Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. стр. 208. ISBN 978-0-7803-4715-1.CS1-одржување: повеќе имиња: список на автори (link)
- ↑ See Eq. 5.10 and discussion in A. G. G. M. Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. стр. 119 ff. ISBN 0-521-82634-9.; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd. изд.). Springer. стр. 261 ff. ISBN 3-540-60443-X.; and Eq. 3.5 in F Mainardi (1996). „Transient waves in linear viscoelastic media“. Во Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy (уред.). Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. стр. 134. ISBN 981-02-4271-9.CS1-одржување: повеќе имиња: список на уредници (link)
- ↑ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. стр. 106. ISBN 0-8176-3635-8.
- ↑ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. стр. 31. ISBN 0-86542-078-5.
- ↑ Seth Stein, Michael E. Wysession (2003). op. cit.. стр. 32. ISBN 0-86542-078-5.
- ↑
Kimball A. Milton, Julian Seymour Schwinger (2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer. стр. 16. ISBN 3-540-29304-3.
Thus, an arbitrary function f(r, t) can be synthesized by a proper superposition of the functions exp[i (k·r−ωt)]...
- ↑ Raymond A. Serway and John W. Jewett (2005). „§14.1 The Principle of Superposition“. Principles of physics (4th. изд.). Cengage Learning. стр. 433. ISBN 0-534-49143-X.
- ↑
Newton, Isaac (1704). „Prop VII Theor V“. Opticks: Or, A treatise of the Reflections, Refractions, Inflexions and Colours of Light. Also Two treatises of the Species and Magnitude of Curvilinear Figures. 1. London. стр. 118.
All the Colours in the Universe which are made by Light... are either the Colours of homogeneal Lights, or compounded of these...
- ↑ M. J. Lighthill; G. B. Whitham (1955). „On kinematic waves. II. A theory of traffic flow on long crowded roads“. Proceedings of the Royal Society of London. Series A. 229: 281–345. Bibcode:1955RSPSA.229..281L. doi:10.1098/rspa.1955.0088.CS1-одржување: ref=harv (link) And: P. I. Richards (1956). „Shockwaves on the highway“. Operations Research. 4 (1): 42–51. doi:10.1287/opre.4.1.42.CS1-одржување: ref=harv (link)
- ↑ A. T. Fromhold (1991). „Wave packet solutions“. Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981. изд.). Courier Dover Publications. стр. 59 ff. ISBN 0-486-66741-3.
(p. 61) ...the individual waves move more slowly than the packet and therefore pass back through the packet as it advances
- ↑ Ming Chiang Li (1980). „Electron Interference“. Во L. Marton & Claire Marton (уред.). Advances in Electronics and Electron Physics. 53. Academic Press. стр. 271. ISBN 0-12-014653-3.
- ↑ See for example Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2. изд.). Springer. стр. 60. ISBN 3-540-67458-6. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. стр. 57. ISBN 0-521-62005-8.,Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Press. стр. 17. ISBN 0-521-65841-1..
- ↑ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd. изд.). World Scientific. стр. 47. ISBN 9971-5-0789-7.
- ↑ Walter Greiner, D. Allan Bromley (2007). Quantum Mechanics (2nd. изд.). Springer. стр. 60. ISBN 3-540-67458-6.
- ↑ Siegmund Brandt, Hans Dieter Dahmen (2001). The picture book of quantum mechanics (3rd. изд.). Springer. стр. 23. ISBN 0-387-95141-5.
- ↑ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers. Cambridge University Press. стр. 677. ISBN 0-521-59827-3.
| „Бран“ на Ризницата ? |
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|


















































