Синусен бран

Синусен бран или синусоида[1][2] — математичка крива која ги опишува непречено периодични осцилација. Синус бран е континуиран бран. Именувана е по синусна функцијата, на која е графиконот. Тоа се случува често во чиста и применета математика, како и во физиката, инженерството, обработката на сигнали и многу други полиња. Својот најосновен облик како функција од времето на вклучување (t) е:
каде што:
- A = на амплитуда , девијација на функцијата од нула.
- F = на обичнита честота , на број на осцилации (циклуси) кои се јавуваат секоја секунда од времето.
- Ω = 2πf , на аголна честота , стапката на промена на аргументот на функцијата во единиците на радијани во секунда
- \ varphi = На фаза , наведува (во радијани), каде што во својот циклус осцилација е на t = 0.
- Кога \ varphi Е не-нула, целите бранови ќе се префрлат во времето од износот \ varphi / Ω секунди. Негативна вредност претставува одлагање, а позитивната вредност претставува напредок.
 |
|
| Проблеми со пуштањето? Помош. | |

Синусен бран е важен во физиката, бидејќи тој ја задржува својата брановидна форма кога се додава уште еден синусен облик на иста честота со произволна фаза и големина. Тоа се само периодични бранови кои го имаат тоа својство. Ова својство е значајно во Фуриерова анализа и го прави акустично(слушно) уникатен.
Општа форма[уреди | уреди извор]
Во принцип, функцијата може да има ':' * просторна променлива x , која ја претставува позицијата "" на димензија на кој се движи бран, и има карактеристичен параметар k кој се нарекува бранов број (или агонален број на бран), што претставува сразмерноста меѓу аголната честота ω и линеарна брзина (брзината на ширење) ν * не- нула центарна амплитуда, D одосно:
- , ако бранот се движи кон десно
- , ако бранот се движи ко лево.
Браовиот број е поврзан со аголната честота со :.
каде λ (ламбда) е бранова должина, f е честота, и V е линеарна брзина. Оваа равенка дава синусен облик за една димензија; генерализирано равенка дадена погоре го дава поместувањето на брановата позиција x на време t по една линија. Со ова може, на пример, да се земе предвид вредноста на бран по должината на жицата.
Во две или три просторни димензии, истата равенка го опишува патувањето авионски бран ако положба x и брановиот број k се претставени како вектори и нивниот производ како dot производот. За посложени бранови, како што се висината на бранот во вода, по фрлање на еден камен,се користат за посложени равенки.
Случувања[уреди | уреди извор]
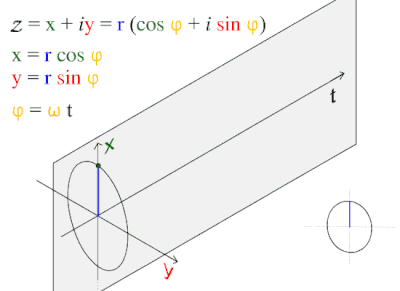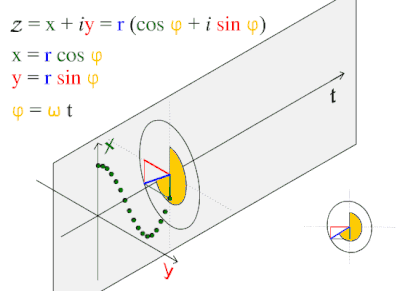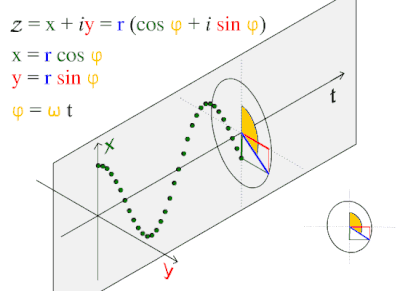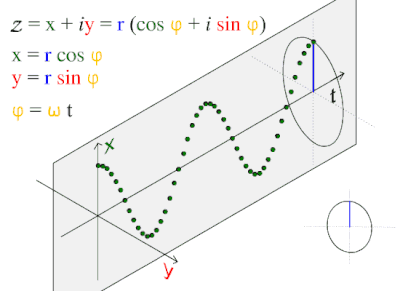
Овој бранов модел е често застапен во природата, вклучувајќи ги ветерните браови,звучите бранови и светлиски бранови. Косиусен бран, е така наречен синусоиден, затоа што , што е исто така синусен бран со фаза на менување од π/2 radians. Заради тоа се семета дека косинусна функција ја води синусната функција, или синусот го забавува косинуот.
Човечкото уво може да се препознае еденинствен синуснен бран кој е јасен и чист затоа што синусните бранови се претставени на една честота без хармонија.
За човечкото уво, звук кој е направен од повеќе синусни бранови ќе има значитело приметлива хармонија. Од друга страна, ако звукот содржи апериодични бранови заедно со синусни бранови (кои се периодични), тогаш звуковите ќе се гледаат "бучни" како бучава се одликува како апериодична.
Фуриеви серии[уреди | уреди извор]

Во 1822 година, францускиот математичар Џозеф Фурие открил дека за синусоидни бранови може да се корисат едноставни блокови за зградата за да се опишат и да се приближат било кои периодични бранови, вклучувајќи ги и квадратите бранови. Фурие го користи како аналитичка алатка во студијата на бранови и топлински проток. Тоа често се користи во обработка на сигналот и статистичка анализа на временски низи.
Патување и стоини бранови[уреди | уреди извор]
Бидејќи синусните бранови шират без да го менуваат својот облик во дистрибуирани линеарни системи, тие често се користат за анализа на браново простирање. Синусните бранови патуваат во две насоки во вселената и тоа можае да се претстави како:
Кога два бранаа имаат иста амплитуда и честота, и патуваат во спротивна насока, superpose едни со други, а потоа стоен бран се создава модел. Имајте на ум дека, на кинење на жици,вмешаите бранови се одбиени браонови од фиксните точки на жицата. Затоа, вертикални бранови се појавуваат само на одредени честоти, кои се наведени како резонантнати на честоти и се составени од фундаментална честота и повисоки хармонии.
Поврзано[уреди | уреди извор]
- Фуриева трансформација
- Хармониски низи
- Хармониски низи
- Хелмхолцова равенка
- Моментна фаза
- Осцилоскоп
- Тон
- Едноставно хармониско движење
- Синусоиден модел
- Бран
- Бранова равенка
Наводи[уреди | уреди извор]
Дополнителна литература[уреди | уреди извор]
- „Sinusoid“. Encyclopedia of Mathematics. Springer. Посетено на December 8, 2013.






