Косинусна теорема

Косинусна теорема (позната и како косинусна формула или косинусно правило) – формула која дава врска меѓу должините на страните на триаголник со косинусот на еден од неговите агли. Користејќи го обележувањето од сл. 1, косинусната теорема е дадена со формулата:
каде го означува аголот меѓу страните од должините и и спротивен на страната со должина . За истата слика, другите две формули се аналогни:
Косинусната теорема ја обопштува Питагоровата теорема, која важи само за правоаголни триаголници: ако аголот е прав агол (90 степени, или радијани), тогаш , па косинусната теорема се сведува на Питагоровата теорема:
Косинусната теорема е кориснa за:
1) пресметување на третата страна на триаголник кога се познати другите две страни и аголот меѓу нив,
2) пресметување на аглите на триаголник кога се познати неговите три страни.
Историја[уреди | уреди извор]

Иако поимот за косинус сè уште не бил развиен во негово време, Евклидовите „Елементи“, кои датираат од III век пр.н.е., содржат рана геометриска теорема која е скоро еднаква на косинусната. Случаите на тапоаголен триаголник и остроаголен триаголник (кои соодветствуваат на двата случаја на негативен и позитивен косинус) се обработени посебно, во тврдењата 12 и 13 од Книга II. Со оглед на тоа дека во времето на Евклид не постоеле тригонометриските функции и алгебрата (особено негативните броеви), неговото тврдење има повеќе геометриски вкус:
Tврдењe 12
Кај тапоаголни триаголници квадратот на страната спротивна на тапиот агол е поголем од збирот на квадратите на страните кои го чинат тапиот агол за двапати по правоаголникот од една од страните на тапиот агол - онаа на која паѓа нормалата и отсечката од правата линија на нормалата кон тапиот агол.— Евклидови „Елементи“.[1]
Користејќи го обележувањето на сл. 2, Евклидовото тврдење може да се претстави со формулата
Оваа формула може да се преобрази во косинусната теорема ако се забележи дека . Tврдењeто 13 го содржи целосно аналогното тврдење за остроаголни триаголници.
Евклидовите „Елементи“ го отвориле патот за откривање на косинусната теорема. Во XV век, Џамшиц ал-Каши, персиски математичар и астроном, ја дал првата експлицитна формулација на косинусната теоремеа погодна за триангулација. Тој направил точни тригонометриски таблици и ја изразил теоремата во погоден облик за современо користење. Во Франција, косинусната теорема сè уште се нарекува „Теорема на Ал-Каши“[2][3][4]
На Запад, теоремата ја популаризирал Франсоа Виет во XVI век. На почетокот на XIX век, современото алгебарско обележување овозможило косинусната теоремa да се запишува во денешниот симболичен облик.
Примени[уреди | уреди извор]

Теоремата се користи при триангулација, за решавање на триаголник или круг, односно за да се најде (види сл. 3):
- третата страна на триаголник, доколку се знаат другите две страни и аголот меѓу нив:
- агол на триаголник, доколку се знаат трите негови страни:
- третата страна на триаголник доколку се знаат двете други страни и аголот спротивен на една од нив (во случај на правоаголен триаголник може да се искористи и Питагоровата теорема):
Овие формули продуцираат големи грешки на заокружување при пресметки со подвижна запирка доколку триаголникот е многу остар, односно ако е релативно мала во однос на и или ако е мал во споредба со 1. Можно е дури да се добие резултат за косинус на агол кој е малку поголем од еден.
Третата прикажана формула е резултат од решавање на во квадратната равенка . Оваa равенка може да има две позитивни решенија, едно позитивно решение или да нема позитивни решенија што соодветстува на бројот на можни триаголници. Ќе има две позитивни решенија ако , само едно позитивно решениe ако , а ќе нема решение ако или .
Докази[уреди | уреди извор]
Со користење на формула за растојание[уреди | уреди извор]
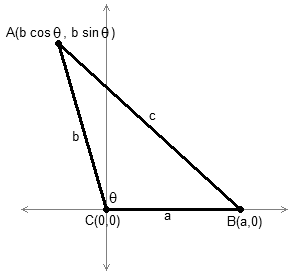
Да разгледаме триаголник со страни со должини , , , каде аголот спротивен на страната со должина е . Овој триаголник може да се смести во Декартов координатен систем со внесување на наведените точки, како што е прикажано на сл. 4:
Според формулата за растојание, имаме
Сега, работиме само со оваа равенка:
Предноста на овој доказ е тоа што не бара да се разгледуваат посебно различните случаи на остроаголен, правоаголен или тапоаголен триаголник.
Со користење тригонометрија[уреди | уреди извор]

Со спуштање на нормала на страната низ точката , т.е. висина на триаголникот (види сл. 5), се добива
Ова е точно и ако или е тап агол, во кој случај подножјето на висината е на продолжението на страната, вон триаголникот. Множејќи со се добива
Земајќи ги предвид другите две висини на триаголникот, се добиваат аналогните равенства
Собирајќи ги левите и десните страни на двете последни равенства, добиваме
Одземајќи ја првата равенка од последната резултира во
што се поедноставува во
Во овој доказ се користи тригонометрија т.ш. се разгледуваат косинусите на различни агли како одделни величини. Тука се користи фактот дека косинусот на агол ја изразува врската помеѓу де страни кои го зафаќаат тој агол во секој правоаголен триаголник. Во други докази, меѓу кои некои се дадени подолу се „погеометриски“ во смисла дека во нив изрази како се користат само како ознака за должина на некоја отсечка.
Многу докази ги третираат случаите на тапи и остри агли γ одвоено.
Со користење на Питагоровата теорема[уреди | уреди извор]
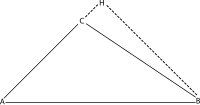
За тап агол[уреди | уреди извор]
Евклид ја докажал косинусната теорема со примена на Питагоровата теорема за секој од двата правоаголни триаголника прикажани на сликата ( и ). Ако со ја обележиме должината на отсечката и со висината , од триаголникот се добива
а од триаголникот се добива
Со развивање на првата равенка се добива
Заменувајќи ја втората равенка во последниот израз, се добива:
Ова е Предлог 12 од Книга 2 од Евклидовите „Елементи“.[5] За да се преобрази ова равенство во современ облик на косинусната теорема, треба да забележиме дека
За остар агол[уреди | уреди извор]
Евклидовиот доказ на неговиот Предлог 13 се одвива според истите линии како неговиот доказ за Предлогот 12: ја применува Питагоровата теорема на двата правоаголни триаголника добиени со спуштање на нормала кон една од страни која го формира аголот γ и ја користи биномната теорема за поедноставување.

Друг доказ за случај на остар агол[уреди | уреди извор]
Со користење тригонометрија, косинусната теорема може да се добие со користење на Питагоровата теорема само еднаш. Фактички, со користење на правоаголниот триаголник на левата страна на сл. 6 може да се покаже дека:
при што го искористивме тригонометрискиот идентитет
Во овој доказ е потребна мала промена ако . Во овој случај, правоаголниот триаголник на кој се применува Питагоровата теорема се поместува надвор од триаголникот . Единствениот учинок што ова го има на пресметката е дека вредноста се заменува со . Со оглед на тоа дека оваа вредност влегува во пресметката само преку нејзиниот квадрат, остатокот од доказот е незасегнат. Овој проблем се јавува само кога аголот е тап и истото може да се избегне со пресликување на триаголникот околу бисектрисата на аголот .
За сл. 6 вреди да се забележи дека ако аголот на спроти страната е , тогаш:
Ова е корисно за директна пресметка на втор агол кога се дадени две страни и аголот меѓу нив.
Со користење на Птоломејовата теорема[уреди | уреди извор]
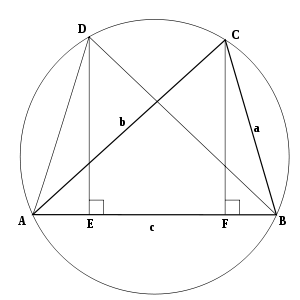
Го гледаме дијаграмот десно. Околу триаголникот со страни , , е опишана кружница како што е прикажано. Го конструираме триаголникот како складен на триаголникот со и . Нормалите од и ја сечат основата во точките и соодветно. Тогаш:
Сега косинусната теорема се изведува со директна примена на Птоломеjoвата теорема на тетивниот четириаголник :
Очигледно е дека ако аголот е прав, тогаш е правоаголник и со примена на Птоломејовата теорема се добива Питагоровата теорема:
Со споредување на плоштини[уреди | уреди извор]
Косинусната теорема може да се докаже и со пресметување на плоштини. Промената на знакот на косинусот кога аголот e тап, изискува потреба од разгледување на различни случаи.
Да се потсетиме дека
- , и се плоштини на квадратите со страни , и , соодветно;
- ако аголот е остар, тогаш е плоштина на паралелограмот со страни и кои образуваат агол ;
- ако аголот е тап, тогаш е негативен, па е плоштината на паралелограмот со страни и кои образуваат агол .
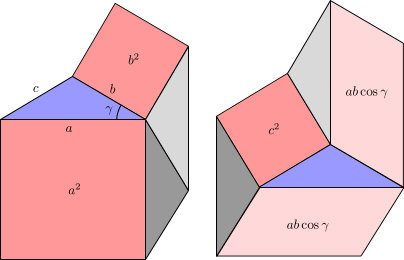
Случај на остар агол. На сликата 7 a е прикажан седумаголник пресечен на помали парчиња (на два различни начина) за да се добие доказ на косинусната теорема. Различните парчиња се:
- во темно розово, плоштините и лево и плоштините и десно;
- во сино, триаголникот , лево и десно;
- во сиво, помошни триаголници, сите конгруентни на , по два (потемен и посветол) на левата и десната слика.
Еднаквоста на плоштините на седумаголниците на сликите лево и десно дава:

Случај на тап агол. На сликата 7 б) шестаголникот се сече на два различни начина на помали парчиња со што се добива доказ на косинусната теорема во случај кога аголот е тап. Имаме
- во розово, плоштините , b2 и лево и десно;
- во сино, триаголникот и триаголник складен на него, лево и десно.
Еднаквоста на плоштините на формите лево и десно дава:
Ригорозниот доказ ќе мора да вклучи докази дека облиците на левите и десните страни се конгруентни и следователно на тоа дека имаат еднакви плоштини. Во него се користи теоријата на конгруентни триаголници.
Со користење на геометрија на круг[уреди | уреди извор]
Со користење на геометрија на круг, може да се даде погеометриски доказ отколку со користење само на Питагоровата теорема. Во овој доказ се избегнуваат алгебарските изведувања (особено биномната теорема).

При остар агол , каде . Се спушта нормала од кон со што се добива правоаголен триаголник со хипотенуза и катета со должина (видете ја сл. 8 а)). Со пресликување на во однос на нормалата, се удвојува правоаголниот триаголник и формира рамнокрак триаголник . Се конструира кружница со центар во и полупречник и негова тангента низ , . Тангентата образува прав агол со полупречникот (Евклидови „Елементи“: Книга III, Тврдење 18), па затоа жолтиот триаголник на сл. 8 а) е правоаголен. Со примена на Питагоровата теорема се добива дека
Потоа со користење на теоремата за тангента-секанта (Евклидови „Елементи“: Книга III, Тврдење 36), според кое квадратот на тангентата низ точката вон кругот е еднаков на производот на двете отсечки (од ) образувани од која било секанта на кружницата која минува низ . Во овој случај: или Со замена во равенката се добива косинусната теорема:
Треба да се забележи дека е степен на точката во однос на кружницата. Користењето на Питагоровата теорема и тангентно-секантната теорема може да се замени со примена само на теоремата за степен на точка во однос на кружница.

Случај на остар агол , каде . Се спушта нормала од кон со што се добива правоаголен триаголник со хипотенуза и катета со должина (видете ја сл. 8б)). Се пресликува правоаголниот триаголник симетрично во однос на нормалата при што оригиналот и сликата го формираат рамнокракиот триаголник . Наредно, се конструира кружница со центар во и полупречник , а потоа се црта тетива низ која е нормална на со должина двапати поголема од . Со примена на Питагоровата теорема се добива:
Сега се користи тетивната теорема (Евклидови Елементи: Книга III, Тврдење 35), која вели дека ако две тетиви се сечат, производот од двете добиени отсечки на едната тетива се еднакви со производот на двете добиени отсечки добиени на другата тетива. Во овој случај имаме или
Со замена на добиениот израз во претходната равенка, се добива косинусната теорема:
Треба да се забележи дека бидејќи точката е во внатрешноста на кружницата, нејзиниот степен во однос на кружницата има негативна вредност,

Случај на тап агол γ. Овој доказ директно ја користи теоремата за степен на точка, без помошни триаголници добиени со конструкција на тангента или тетива. Се конструира кружница со центар и полупречник (видете ја слика 9), која ја сече секантата која минува низ и во и . Степенот на точката во однос на кружницата е еднаков на и . Оттука,
што е косинусната теорема.
Со користење на алгебарски мерки за отсечки (кои дозволуваат негативни броеви за должини на сегментите) случајот на тап агол () и остар агол () може да се разгледуваат истовремено.
Со користење на синусната теорема[уреди | уреди извор]
Со користење на синусната теорема и знаејќи дека збирот на аглите во триаголник мора да биде 180 степени, се добива следниов систем равенки (трите непознати се аглите):
Ако се изрази аголот од третата равенка и добиениот израз го замениме во првите две равенки, и ако се искористи тригонометриското својство дека синус од суплементен агол е еднаков на синусот од самиот агол, се добива еквивалентниот систем:
Со користење на идентитетот
се добива еквивалентниот систем
Сега, ако се поделaт првата и втората равенка со , се добива:
Следствено, од првата равенка на системот, имаме
- а од втората равенка, со квадрирање се добива
Сега, со замена на последниот израз во втората равенка и со користење на идентитетот:
се добива една равенка со една непозната:
Множејќи со , се добива следнава равенка:
Со развивање на квадратот на биномот, имаме
и со користење на Питагоровиот идентитет се добива:
Со користење на вектори[уреди | уреди извор]
Означуваме
Оттука,
Ако се земе скаларен производ на секоја од страните со самата себе, имаме:
Со користење на идентитетот
се добива
со што е добиено она што се бараше.
Кај рамнокрак триаголник[уреди | уреди извор]
Кога односно, ако триаголникот е рамнокрак и двете еднакви страни го формираат аголот , косинусната теорема значително се поедноставува. Имено, бидејќи , косинусната теорема станува:
или
Аналогна теорема за тетраедри[уреди | уреди извор]
Аналогно тврдење се добива ако се земат , , , да бидат површини на четирите ѕида на тетраедар. Се означуваат диедарските агли (аглите помеѓу два ѕида) со итн. Потоа[6]
Верзија погодна за мали агли[уреди | уреди извор]
Кога аголот, на пример , е мал и страните кои го формираат, и , се со слични должини, при работа со приближни вредности може да се случи во десната страна на стандардниот облик на косинусната теорема да се појават огромни грешки како резултат на искористеното заокружување. Во ситуации кога ова има битно влијание може да се искористи, математичката еквивалентна верзија на косинусната теорема, слична на хаверсинусната формула, :
Во граничен случај при бесконечно мал агол, косинусната теорема дегенерира во формула за должина на кружен лак, .
Во сферната и хиперболичната геометрија[уреди | уреди извор]

Верзии кои се слични на косинусната теорема за Евклидова рамнина важат и во случај на единична сфера и во хиперболична рамнина. Во сферната геометрија, триаголник е дефиниран со три точки u, v и w на единична сфера, и лаковите на големите кружници кои ги спојуваат овие точки. Ако овие големи кружници формираат агли , , , со спротивните страни , , , соодветно, тогаш сферната косинусна теорема тврди дека важат следниве два односa:
Во хиперболичната геометрија, парот равенки е познат како хиперболична косинусна теорема. Првата е:
каде и се хиперболичен синус и косинус, а втората е:
Како во Евклидвата геометрија, и во овие два случаја може да се искористи соодветната форма на косинусната теорема за да се одредат аглите , , од познавањето на страните , , . Спротивно на Евклидовата геометрија, можно е и обратното во двата неевклидови модела: од аглите , , да се определат страните , , .
Унифицирана формула за површини со константна закривеност[уреди | уреди извор]
Со дефинирање две функции и како
- and
се овозможува да се унифицираат формулите за рамнина, сфера и псевдосфера во единствениот облик:
Во ова обележување е комплексен број, кој го претставува полупречникот на закривеност на површината.
- за површината е сфера со полупречник , а неговата константна закривеност е
- за површината е псевдосфера на (имагинарен) полупречник со константа на закривеност еднаква на
- кога , површината се стреми кон Евклидова рамнина, со константа на закривеност еднаква на нула.
Верификација на формулата за неевклидова геометрија
Во првите два случаи, и се добро дефинирани во целата комплексна рамнина за сите и прибирањето на претходните резултати е едноставна.
Оттука, за сфера со полупречник
- .
Слично, за псевдосфера со полупречник
Навистина, and
Потврдување на формулата при граничната вредност на Евклидовата геометрија
Во Евклидовата рамнина мора да се пресметаат соодветните граници за горенаведената равенка:
и
- .
Со примена на ова во општата формула за конечно се добива:
Ако се соберат членовите, се помножат со и се земе , се добива очекуваната формула:
Поврзано[уреди | уреди извор]
- Синусна теорема
- Тангенсна теорема
- Котангенсна теорема
- Список на тригонометриски идентитети
- Молвајдева формула
- Триангулација
Наводи[уреди | уреди извор]
- ↑ „Euclid, Elements Thomas L. Heath, Sir Thomas Little Heath, Ed“.
- ↑ Clifford A. Pickover (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. стр. 106.
- ↑ Igarashi, Yoshihide. Computing : a historical and technical perspective. Boca Raton, Florida. стр. 78. ISBN 9781482227413. OCLC 882245835.
- ↑ Ilija Baruk (2008). Causality I. A Theory of Energy, Time and Space, Volume 2. стр. 174.
- ↑ Java applet version by Prof. D E Joyce of Clark University.
- ↑ Casey, John (1889). A Treatise on Spherical Trigonometry: And Its Application to Geodesy and Astronomy with Numerous Examples. London: Longmans, Green, & Company. стр. 133.
Надворешни врски[уреди | уреди извор]
- Хацевинкел, Михил, уред. (2001), „Cosine theorem“, Математичка енциклопедија, Шпрингер, ISBN 978-1556080104
- Several derivations of the Cosine Law, including Euclid's at cut-the-knot
- Interactive applet of Law of Cosines






























































































































































![{\displaystyle {\begin{aligned}1-{\frac {BC^{2}}{2R^{2}}}+o\left({\frac {1}{R^{4}}}\right)={}&\left(1-{\frac {AB^{2}}{2R^{2}}}+o\left({\frac {1}{R^{4}}}\right)\right)\cdot \left(1-{\frac {AC^{2}}{2R^{2}}}+o\left({\frac {1}{R^{4}}}\right)\right)+\\[5pt]&{}+{\frac {1}{R^{2}}}\left(AB+o\left({\frac {1}{R^{3}}}\right)\right)\cdot \left(AC+o\left({\frac {1}{R^{3}}}\right)\right)\cdot \cos({\widehat {BAC}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1285bf03dc405127679e17c3b8624927f640f411)

