е (број)

e — математичка константа, приближно еднаква на 2,71828, и единствен реален број, чијашто функција ex има иста вредност на наклонот на тангентата за сите вредности на x.[1] Појасно, единствените функции, кои се еднакви на сите свои изводи се во облик Cex, каде C е константа.[2] Функцијата ex е наречена експоненцијална функција и нејзината инверзна функција е природниот логаритам или логаритам со основа e. Бројот e обично е дефиниран како основа на природниот логаритам (дефиницијата со примена на интеграл се користи подоцна) како гранична вредност на секоја низа или како збир на сите редови (видете прикажување на е).
Бројот e е еден од најважните броеви во математиката,[3] паралелно со додатните и мултипликативни идентитети 0 и 1, константата π и имагинарната единица i.
Бројот e понекогаш се нарекува „Ојлеров број“, по името на швајцарскиот математичар Леонард Ојлер. (e не треба да се меша со γ – Ојлер-Маскерониевата константа - понекогаш наречена Ојлерова константа.)
Бројот e е трансцендентен и поради тоа ирационален, односно неговата вредност не може да се пресмета во ограничен број на децимали или, пак, во децимали кои се повторуваат. Бројчената вредност на e, заокружена на 20 децимали е 2,71828 18284 59045 23536….
Историја[уреди | уреди извор]
Првите знаци за појавата на бројот се појавиле во 1618 во табелата со додатоци од работа на логаритмите од страна на Џон Непер.[4] И покрај тоа, ова не ја содржело константата, туку едноставно список на природни логаритми пресметани од константата. Се смета дека табелата била напишана од Вилијам Отред. „Откривањето“ на константата му се припишува на Јакоб Бернули, кој се обидел да ја најде вредноста на следниот израз (што всушност е e):
Првата позната примена на константата, претставена со буквата b била во дописот од Готфрид Лајбниц до Кристијан Хајгенс во 1690 и 1691. Леонард Ојлер започнал да ја употребува буквата e за ознака на константата во 1727 година и првата употреба на буквата e била во Ојлеровата Механика (1736). Додека во следните години некои истражувачи ја употребувале буквата c, буквата e била повообичаена и станала стандардна ознака на бројот.
Примена[уреди | уреди извор]
Проблемот на сложена камата[уреди | уреди извор]
Јакоб Бернули ја открил константа, анализирајќи го прашањето за сложената камата.
Еден прост пример е пресметката, која започнува со $1,00, за кој се плаќа 100% камата годишно. Ако каматата се плаќа еднаш на крајот од годината, тогаш сумата која треба да се плати е $2,00; но ако каматата се пресметува двапати во годината, сумата од еден $1 се множи двапати со 1,5, односно $1,00×1,5² = $2,25. Доколку камата се пресметува квартално, тогаш $1,00×1,254 = $2,4414…, а ако тоа се пресметува секој месец, $1,00×(1,0833…)12 = $2,613035….
Бернули открил дека граничната вредност на низата (сложени камати) за сè помали интервали расте со помал интензитет. Вкаматувањето неделно изнесува $2,692597…, додека дневно $2,714567…. Доколку бројот на интервали на вкаматувањето е n, со камата од 1/n во секој интервал, тогаш граничната вредност е број кој е еднаков на e, односно со континуиран раст вредноста којашто се достигнува е $2,7182818…. Поедноставно, доколку вкаматувањето започнува од $1, а се враќаат (1+R) долари со проста камата, тогаш со континуелно вкаматување ќе се пресметаат eR долари.
Бернулиевите обиди[уреди | уреди извор]
Бројот e има примена и во теоријата на веројатност, каде расте на начин кој очигледно не е поврзан со експоненциојалниот пораст. Да претпоставиме дека комарџија игра на машина која исплаќа со веројатност од еден од n и игра n пати. Тогаш, за поголема вредност, на n (на пр. милион) веројатноста дека комарџијата нема да добие ништо е отприлика 1⁄e.
Ова е пример од Бернулиевите обиди. Секој пат кога комарџијата ќе се реши да игра, шансата за добивка е еден во милион. Играјќи милион пати, според биномната распределба, која е поврзана со биномната теорема. Веројатноста да се добие k пати од милион обиди е;
Впрочем, веројатноста да се добие 0 пати (k=0) е
Ова е поврзано со граничната вредност на 1⁄e:
Дисмутации[уреди | уреди извор]
Друга примена на e е исто така откриена од Јакоб Бернули, но заедно со Пјер Ремон де Монмор и претставува проблем на дисмутации, познат и како проблем на проверка на капата.[5] Овде,n гости се повикани на забава и пред вратата секој гостин ја проверува капата со домаќинот, кој потоа ги става во обележани кутии. Но, домаќинот не го знае името на гостинот, па мора да ги стави во случајно одбрани кутии. Проблемот на Де Монмор е: која е веројатноста дека ниту една од капите не е ставена во вистинската кутија. Одговорот е:
Како што бројот на гости n се движи кон бесконечност, pn се стреми кон 1⁄e. Освен тоа, бројот на начини капите да се ставени во кутиите, така што ниту една од капите да не е ставена во вистинската кутија е точно n!⁄e, заокружено на најблискиот цел број.[6]
Асимптотска анализа[уреди | уреди извор]
Бројот e природно се појавува во поврзаноста со многу проблеми, вклучувајќи ги и оние во асимптотската анализа. Познат пример е Стирлинговата формула за пресметување на факториел на многу големи броеви, во која се употребуваат и бројот e и π:
- Од ова следува дека
e во анализата[уреди | уреди извор]
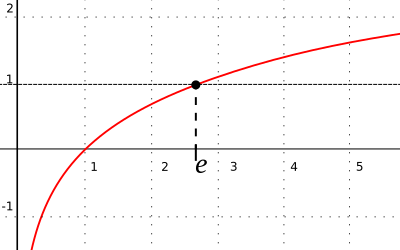
Основно образложение за воведување на бројот e во математичката анализа е за да може да се олесни пресметувањето на изводи и интеграли од експоненцијални функции и логаритми.[7] Типичната експоненцијална функција y=ax има извод, претставен како асимптотска вредност:
Асимптотската вредност на десната страна е независна од променливата x: таа зависи само од основата a. Кога основата е e, оваа асимптотска вредност е еднаква на 1, па e симболички се претставува со равенството:
Како последица на ова, експоненцијалната функција со основа e особено се применува во математичката анализа. Избирајќи го бројот e, наместо некој друг број од експоненцијалните функции, пресметките за добивање на извод стануваат многу полесни.
Друго образложение доаѓа од разгледувањето на логаритам со основа a.[8] Разгледувањето на дефиницијата за извод од logax како асимптотска вредност:
каде замената u = h/x е направена во последниот чекор. Последното појавување на асимптотска вредност во оваа пресметка е повторно неопределена асимптотска вредност, која зависи само од основата a и ако основата е e, тогаш асимптотска вредност е еднаква на 1. Симболично,
Логаритмот со основа е е наречен природен логаритам, кој често се обележува со „ln“ и често се однесува на диференцијацијата, додека нема недетерминирана асимптотска вредност за време на пресметките.
Има два начини, во кои се претставува a=e. Едниот е да се пресмета извод од експоненцијалната функција ax за ax. Другиот е да се пресмета извод од логаритам од 1/x со основа a. И во двата случаи доаѓа до соодветен избор на основата за пресметка на изводите. Всушност, овие две основи го содржат бројот e.
Алтернативни карактеризирања[уреди | уреди извор]
Можни се и други карактеризирања на бројот e: една е асимптотската вредност на низа, другата е збир од редови, а другите се поврзани со интегралите. Одамна биле воведени следните два еквиваленти:
1. Бројот e е единствен позитивен реален број за кој важи
2. Бројот e е единствен позитивен реален број за кој важи
Следните три карактеризирања на експоненцијалната функција се еквивалентни:
3. Бројот e е асимптотска вредност
Слично:

4. Бројот e е збир на редови
каде n! е факториел од n.
5. Бројот e е единствениот позитивен реален број за кој важи
- .
Својства[уреди | уреди извор]
Анализа[уреди | уреди извор]
Како и во образложението, експоненцијалната функција f(x) = ex е значајна, бидејќи е единствена нетривијална функција, која има извод еднаков на самата функција.
и поради тоа нејзиниот неопределен интеграл е:
Експоненцијална функција[уреди | уреди извор]
Нека бројот x = e, каде екстремот се појавува за функцијата:
Поедноставно, x = n√e е каде екстремот се појавува за функцијата
Бесконечната тетрација
конвергира само ако e−e ≤ x ≤ e1/e, според теоремата на Леонард Ојлер.
Теорија на броеви[уреди | уреди извор]
Реалниот број e е ирационален (видете доказ дека e е ирационален број) и трансцендентен (Линдеман-Ваерштрасова теорема). Тоа е првиот број за кој се докажало дека е трансцендентен без да биде разложуван за таа цел (споредба со Лиувиовиот број); доказот бил направен од страна на чарлс Хермит во 1873. Бројот е хипотетички е нормален.
Комплексни броеви[уреди | уреди извор]
Експоненцијалната функција ex може да биде запишана и со примена на Тејлоровиот ред
Бидејќи редот има многу значајни својства за ex дури и кога x е комплексен број, вообичаено се употребува за да се укаже на дефиницијата за ex до комплексните броеви. Ова со Тејлоровиот ред за sin и cos x, доведува до докажување на Ојлеровата формула:
што важи за сите x. Специјален случај е кога x = π, кој е познат како Ојлеров идентитет:
Како последица на ова
од што следува во основниот вид на логаритам
Освен тоа, примената на законите за степенување,
ја чинат Моавровата формула.
Случајот
обично е познат како Cis(x).
Диференцијални равенки[уреди | уреди извор]
Основната функција
е решението на диференцијалната равенка:
Претставувања[уреди | уреди извор]
Бројот e може да биде претставен како реален број на различни начини: како бесконечен ред, бесконечен производ, бесконечна дропка или гранична вредност на низа. Основното меѓу овие претставувања, делумно во воведот од математичката анализа е граничната вредност
дадена погоре, како и редот
даден со изведување на редот за ex за x=1.
Можни се и други понеобични претставувања. На пример, e може да биде претставен како бесконечна дропка:
Или во пократката формула:
којашто може да биде запишана хармонично со додавање на 0:[9]
Многу други редови, низи, бесконечни дропки и бесконечни производи биле развиени како претставувања на e.
Стохастички претставувања[уреди | уреди извор]
Покрај детерминистичките аналитички изрази за претставувањето на e, кои се опишани погоре, постојат неколку схоластички протоколи за пресметување на e. Во еден таков протокол, случајните примери од n од непрекинатата рамномерна прераспределба на (0, 1) се применуваат за пресметување на e. Ако
тогаш очекувањето за U е e: .[10][11] Освен тоа, едноставниот просек на U променливите е отприлика e.
Познати децимали[уреди | уреди извор]
Бројот на познати децимали на e драматично се зголемувал во последните неколку декади. Ова е поради подобрувањето на можностите на компјутерите, како и на напредокот на алгоритмите.[12][13]
| Година | Децимали | Пресметал |
|---|---|---|
| 1748 | 18 | Леонард Ојлер[14] |
| 1853 | 137 | Вилијам Шенкс |
| 1871 | 205 | Вилијам Шенкс |
| 1884 | 346 | Маркус Бурман |
| 1946 | 808 | ? |
| 1949 | 2.010 | Џон фон Нојман (на ENIAC) |
| 1961 | 100.265 | Даниел Шенкс и Џон Френч |
| 1981 | 116.000 | Стивен Гери Вознијак (на Apple II[15]) |
| 1994 | 10.000.000 | Роберт Немирог и Џери Бонел |
| 1997 (мај) | 18.199.978 | Патрик Демикел |
| 1997 (август) | 20.000.000 | Биргер Зајферт |
| 1997 (септември) | 50.000.817 | Патрик Демикел |
| 1999 (февруари) | 200.000.579 | Себастијан Веденивски |
| 1999 (октомври) | 869.894.101 | Себастијан Веденивски |
| 1999 (21 ноември) | 1.250.000.000 | Хавиер Гурдон |
| 2000 (10 јули) | 2.147.483,648 | Шигеру Кондо и Хавиер Гурдон |
| 2000 (16 јули) | 3.221.225.472 | Колин Мартин и Хавиер Гурдон |
| 2000 (2 август) | 6.442.450.944 | Шигеру Кондо и Хавиер Гурдон |
| 2000 (16 август) | 12.884.901.000 | Шигеру Кондо и Хавиер Гурдон |
| 2003 (21 август) | 25.100.000.000 | Шигеру Кондо и Хавиер Гурдон |
| 2003 (18 септември) | 50.100.000.000 | Шигеру Кондо и Хавиер Гурдон |
| 2007 (27 април) | 100.000.000.000 | Шигеру Кондо и Стив Паљаруло |
Информатичка технологија[уреди | уреди извор]
Во современата интернет култура, поединци и организации имаат почит кон бројот e.
На пример, во IPO картотеката за Google, во 2004, наместо некој стандарден број на пари, компанијата ја соопшти својата намера да достигне $2,718,281,828, што се e милијарда долари. Компанијата Google беше одговорна и за мистериозната рекламна табла [16] која се појави во срцето на Силициумската Долина, а подоцна и во Кембриџ, Масачусетс; Сиетл, Вашингтон; и Остин, Тексас. Можеше да се прочита {first 10-digit prime found in consecutive digits of e}.com. Решавањето на овој проблем и посетувањето на рекламираното мрежно место водело до уште поголем проблем, којшто води до лабораториите на Google, каде посетителот е повикан да поднесе резиме.[17] Првите 10 децимали на бројот e се 7427466391, ред што започнува и од 99-тата децимала[18]
Во друг пример, еминентниот информатичар Доналд Кнут пуштил верзија на броеви на својот програм METAFONT пристапувајќи до e. Верзиите се 2, 2,7, 2,71, 2,718 итн.
Наводи[уреди | уреди извор]
- ↑ Keisler, H.J. Derivatives of Exponential Functions and the Number e
- ↑ Keisler, H.J. General Solution of First Order Differential Equation
- ↑ Howard Whitley Eves (1969). An Introduction to the History of Mathematics. Holt, Rinehart & Winston.
- ↑ O'Connor, J.J., and Roberson, E.F.; The MacTutor History of Mathematics archive: "The number e"; University of St Andrews Scotland (2001)
- ↑ Grinstead, C.M. and Snell, J.L. Introduction to probability theory Архивирано на 27 јули 2011 г. (published online under the GFDL), p. 85.
- ↑ Knuth (1997) The Art of Computer Programming Volume I, Addison-Wesley, p. 183.
- ↑ See, for instance, Kline, M. (1998) Calculus: An intuitive and physical approach, Dover, section 12.3 "The Derived Functions of Logarithmic Functions."
- ↑ This is the approach taken by Klein (1998).
- ↑ Hofstadter, D. R., "Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought" Basic Books (1995)
- ↑ Russell, K. G. (1991) Estimating the Value of e by Simulation The American Statistician, Vol. 45, No. 1. (Feb., 1991), pp. 66-68.
- ↑ Dinov, ID (2007) Estimating e using SOCR simulation, SOCR Hands-on Activities (retrieved December 26, 2007).
- ↑ Sebah, P. and Gourdon, X.; The constant e and its computation
- ↑ Gourdon, X.; Reported large computations with PiFast
- ↑ New Scientist 21 јули 07, стр. 40
- ↑ Byte Magazine, том 6, бр. 6 (јуни 1981) стр. 392) "The Impossible Dream: Computing e to 116,000 places with a Personal Computer"
- ↑ First 10-digit prime found in consecutive digits of e - Brain Tags
- ↑ Shea, Andrea. „Google Entices Job-Searchers with Math Puzzle“. NPR. Посетено на 2007-06-09.
- ↑ Kazmierczak, Marcus (2004-07-29). „Math : Google Labs Problems“. mkaz.com. Архивирано од изворникот на 2010-09-23. Посетено на 2007-06-09.
Наводи[уреди | уреди извор]
- Maor, Eli; e: The Story of a Number, ISBN 0-691-05854-7
Надворешни врски[уреди | уреди извор]
- [мртва врска] The number e to 1 million places and 2 and 5 million places
- Earliest Uses of Symbols for Constants
- e the EXPONENTIAL - the Magic Number of GROWTH Архивирано на 3 март 2009 г. - Keith Tognetti, University of Wollongong, NSW, Australia
- An Intuitive Guide To Exponential Functions & e
- "The story of e", by Robin Wilson at Gresham College, 28 февруари 2007 (available for audio and video download)
- Class Library for Numbers (part of the GiNaC distribution) includes example code for computing e to arbitrary precision.
| Статијата „Е (број)“ е избрана статија. Ве повикуваме и Вас да напишете и предложите избрана статија (останати избрани статии). |
| ||||||||||||
|







![{\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce0cd8eb0003d22f6e68f69c95cf434c43bebc58)





























![{\displaystyle e=[[2;1,{\textbf {2}},1,1,{\textbf {4}},1,1,{\textbf {6}},1,1,{\textbf {8}},1,\ldots ,1,{\textbf {2n}},1,\ldots ]],\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da243a0c3fb854ec732dc08494e07c2827ffb92c)
![{\displaystyle e=[[1,{\textbf {0}},1,1,{\textbf {2}},1,1,{\textbf {4}},1,1,{\textbf {6}},1,\ldots ]].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f191a0e3c4839b2fb99619d32a21598188506bdb)



