Биномна распределба
| Биномна распределба | |
|---|---|
 Закон на распределба (pdf) | |
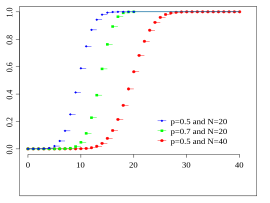 Кумулативна распределба (cdf) | |
| Тип | Дискретна |
| Означување | B(n, p ) |
| Параметри | p∈[0,1] = веројатност на успех по опит, n∈ℕ = број повторување на опитот |
| Поддршка | k∈{0,1,2,...,n} |
k=0,1,2,...,n | |
| CDF | |
| μ | np |
| σ2 | np(1 − p) |
| Асиметрија | |
| Сплоснатост | |
Биномна распределба B(n, p ), n∈ℕ, p∈(0,1) — случаен опит во веројатностa и статистиката, кој се повторува n пати Бернулиев опит со веројатност на успех p запишувајќи го бројот k на успеси во n-тите повторувања.[1]
Одлики на биномната распределба B(n,p)[уреди | уреди извор]
- Биномна распределба е потполно определена со веројатноста на успехот p на Бернулиевиот опит заедно со бројот на повторувања n.
- Биномна распределба е дискретна распределба со дискретната случајна променлива со n+1 елементи: X={0,1,2,...,n}.
- Pr(X=k) е веројатноста на k успеси во n повторувања на Бернулиевиот опит со веројатноста на успех p, k∈X.
Пример: B(5;0,8).
B(5;0,8) значи биномен опит каде што се повторува n=5 пати Бернулиев опит со p=0,8. Има n+1=5+1=6 исходите, т.е. случајната променлива е X={0,1,2,3,4,5}. Елементот k=0 на Х е исходот каде што во 5-те повторувања на Бернулиевиот опит, немале ниту еден успех, елементот k=1 е каде што имало точно еден успех, ..., а елементот k=5 е каде што во 5-те повторувања на опитот сите биле успешни.
Во табелата се наведени сите подредени исходи (пишувајќи 0 за неуспех, а 1 за успех како што е вообичаено за Бернулиев опит). Овие не се исходи на биномниот опит, бидејќи во опитот редоследот не е важен. Тука само гледаме на колку начини можат да се добијат k успеси во n повторувања. На пример, има само еден начин да се добие k=0, односно сите исходи на опитот да се неуспеси 00000.
| k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 00000 | 10000 | 11000 | 00111 | 01111 | 11111 | |
| 01000 | 10100 | 01011 | 10111 | |||
| 00100 | 10010 | 01001 | 11011 | |||
| 00010 | 10001 | 01110 | 01110 | |||
| 00001 | 01100 | 10011 | 11110 | |||
| 01010 | 10101 | |||||
| 01001 | 10110 | |||||
| 00110 | 11001 | |||||
| 00101 | 11010 | |||||
| 00011 | 11100 | |||||
| # | 1 | 5 | 10 | 10 | 5 | 1 |
- Во последниот ред од табелата e запишан бројот на подредените исходи во таа колона. Гледаме дека тој број го следи т.н. биномен коефициент
- каде што знакот ! значи факториел, т.е. n!=n·(n-1)·(n-2)...·(2)·(1) (види и комбинаторика).
- Од друга страна, бидејќи секое повторување на Бернулиевиот опит е независно од минатите како и од идните повторувања, веројатноста на секој подреден исход со k успеси во n повторувања е
- .
Следува дека веројатноста на секоја елемент k на Х e производот на овие два броја, односно
Се разбира дека може да се докаже дека збирот на веројатностите е 1.[2]
Распределби на биномна распределба[уреди | уреди извор]
- Биномен опит B(n,p) ја има дискретната случајна променлива: X={0,1,...,n}.
Закон на распределба - PDF на B(n,p)[уреди | уреди извор]
| PDF на B(n,p) | ||
|---|---|---|
| X=k | Биномен коефициент | Pr(X=k)=f(k) |
| 0 | ||
| 1 | ||
| 2 | ||
| ... | ... | ... |
| n | ||
Кумулативна распределба - CDF на B(n,p)[уреди | уреди извор]
Бидејќи при собирање на соодветните веројатности во општа форма не доаѓа до некоја скратена форма ги даваме само неколку.
| CDF на B(n,p) | ||
|---|---|---|
| x∈ℝ | F(x) | |
| x<0 | 0 | |
| 0≤x<1 | (1-p)n | |
| ... | ... | |
| x≥n | 1 | |
Мерки на биномен опит[уреди | уреди извор]
- Очекувана вредност E(x) [3]
- Дисперзија σ2 [4]
Примери[уреди | уреди извор]
Пример (прод.): B(5,0.8) Приказ на распределбите, ...
| Очекувана вредност: | E(x)=np=5·0,8=4 |
| Дисперзијата е: | σ2=np(1-p)=5·0,8·0,2=0,8 |
| Стандардното отстапување е: | σ ≈ 0,89 |
Пример: Еден стрелец има веројатност p=0,8 да ја погоди целта. Колку е веројатноста во пет стрелања стрелецот да ја погоди целта барем 3 пати? Одговор: B(5;0,8) и 1-Pr(x<3)=1-0,0579=0,9421=94,2%.
Претставување на биномната распределба со Геогебра[уреди | уреди извор]
За графички приказ на PDF-от, т.е. законот на распределба и на CDF-от, т.е. кумулативна распределба на биномна распределба може да се користи бесплатниот софтвер Геогебра.[5]
Дефиниции специфични за биномната распределба се:
n=10 (или соодветен лизгач)
p=0,8 (или соодветен лизгач)
N=n+1
list1=Sequence[k-1,k,1,N] Ја дефинира list1 со елементите на случајната променлива.
list2=Sequence[BinomialCoefficient[n, k] p^(k) (1 - p)^(n - k), k, 0, n] Ја дефинира list2 со веројатностите.
Соодветните наредби на македонски (внимавате на кирилица и латиница) се:
листа1=Низа[k-1,k,1,N]
листа2=Низа[БиноменКоефициент[n, k] p^(k) (1 - p)^(n - k), k, 0, n]
Понатамошните дефиниции се исти за сите дискретни случајни променливи (види дискретна случајна променлива).
Наводи[уреди | уреди извор]
- ↑ Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, "Binomial distribution"“ (PDF) (англиски). Addison-Wesley. стр. 92. Посетено на 1 септември 2013.
- ↑ „Proof of PMF of Binomial Distribution“ (англиски). Архивирано од изворникот на 2012-04-04. Посетено на 1 ноември 2013.
- ↑ „Proof of Expectation of Binomial Distribution“ (англиски). Посетено на 1 ноември 2013.
- ↑ „Proof of Variance of Binomial Distribution“ (англиски). Посетено на 1 ноември 2013.
- ↑ Стојановска, Л (2013). „Биномна Распределба“. Архивирано од изворникот на 2016-03-05. Посетено на 1 October 2013. интерактивен
Поврзано[уреди | уреди извор]
Надворешни врски[уреди | уреди извор]
- Стојановска, Л (2013). „Биномна Распределба“. Архивирано од изворникот на 2016-03-05. Посетено на 1 October 2013. интерактивен
- Geogebra Institute и Институт за Геогебра на МКД (превод) (2013). „Геогебра наредба: Биномна Распределба“. Посетено на 1 November 2013.
- Bogomolny, Alexander (2007). „Binomial Distribution“ (англиски). cut-the-knot.org. Посетено на 1 October 2013. интерактивен
- Lane, D. M., (Editor) (2013). „Online Statistics Education: An Interactive Multimedia Course of Study“ (англиски). Посетено на 1 October 2013.CS1-одржување: излишен текст: список на автори (link)
- Leemis, L. (2007). „Univariate Distribution Relationships“ (англиски). William and Mary, VA, USA. Посетено на 1 October 2013.
- „Binomial Distribution with R-programming Language“ (англиски). Посетено на 1 October 2013. со алгоритми за генерирање на случајни податоци
| ||||||||||
|




















