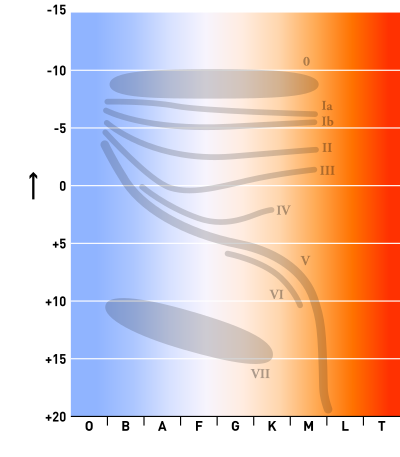
Херцшпрунг-Раселов дијаграм

Херцшпрунг-Раселов дијаграм — дијаграм кој ја покажува врската меѓу апсолутната величина, сјајноста, класификацијата и делотворната температура на ѕвездите. Дијаграмот бил создаден околу 1910^[1] година од страна на Ејнар Херцшпрунг и Хенри Норис Расел, по кои го добил и своето име. Овој дијаграм претставувал голем чекор напред во разбирањето на ѕвездениот развој.

Дијаграмот овозможува (можеби не секогаш точно) да се пронајде апсолутната големина по ѕвездената класа. Особено за ѕвездените класи од О-F. За подоцнежните класи се јавува потребата да се направи избор меѓу џиновите и џуџињата. И покрај тоа, определувањето на разликите на интензивноста на некои линии дозволуваат уверено да се направи тој избор.^[2]

Форми на дијаграмот

Има неколку форми на Херцшпрунг-Раселовиот дијаграм и номенклатурата не е многу добро дефинирана. Оригиналниот дијаграм ја изложува спектралната класификација на ѕвездите на хоризонталната оска, а апсолутната величина на вертикалната оска. Првата големина (т.н.спектрален вид) е тешко јасно да се детерминира и поради тоа често е преместена си бојниот показател B-V на ѕвездите. Овој вид на дијаграм е наречен Херцшпрунг-Раселов дијаграм, или обоеновеличински дијаграм и често се користи од страна на истражувачите. И покрај тоа обоеновеличинскиот дијаграм се користи во некои случаи да се опише дејството со вертикалнта оска, со влијание на привидната, отколку апсолутната величина. Друга форма на дијаграмот дејствува на делотворната температура на ѕвездата на една оска и сјајноста на ѕвездата на другата оска. Ова е тоа што теоретичарите го пресметуваат со помош на компјутерски модели, кои ја опишуваат развојот на ѕвездите. Овој дијаграм би требало да се вика температурно-сјајносен дијаграм, но овој термин многу ретко се користи, бидејќи терминот Херцшпрунг-Раселов дијаграм се смета за посоодветен во екојдневната употреба. Поради негои забуни во поглед на номенклатурата, астрофизичарите прават голема разлика меѓу овие видови на дијаграми.

Причината за овие разликувања е дека точната трансформација од едниот до другиот не е безначајна и зависи од ѕвездено-атмосферскиот модел којшто е користен и неговите параметри (како металичност и притисок, одвоени од температура и сјајност). Исто така, потребно е да се знае растојанието до откриените објекти и меѓуѕвезденото поцрвенување. Емпириските трансформации меѓу различни бојни показатели и делотворни температури се достапшни во литературата (Секигучи 2000, Casagrande 2006).

Херцшпрунг-Раселовиот дијаграм може да се користи и при дефинирањето на различните видови на ѕвезди до еднаквоста на ѕвездениот развој со примена на компјутерски модели, со онаа од истражувањата на истите ѕвезди. Тогаш е потребно, тоа да се замени, или пресметаните големини со откриенити или обратно, откриените големини со пресметаните, така воведувајќи ја нерешителноста.

Карактеристични подрачја

Главна низа

Дијаграмот покажува најмногу ѕвезди спротивно од т.н. главна низа, кои од О-ѕвездите со апсолутна величина од околу −6 до М-ѕвездите со апсолутна величина од 9–16. Ѕвездите од главната низа ја сочинуваат светлосната класа V.

Сонцето е ѕвезда од главната низа во ѕвездената класа G2. Други примери за ѕвезди од главната низа се Вега (А0) и Сириус (А1).

Низа на џинови

Покрај тоа, дадена е и втората разбирлива низа, во која се дадени ѕвездите класифицирани од G0 до M, кои имаат апсолутна величина од 0. Ѕвездите во оваа низа, во споредба со ѕвездите од главната низа со иста ѕвездена класификација (иста температура и светлост на површината) имаат голема апсолуртна величина и посветла површина. Тие исто така имаат поголем пречник од ѕвездите во главната линија и стануваат џиновски ѕвезди. Тие ја сочинуваат т.н. низа на џинови. Ѕвездовите во линијата на џиновски ѕвезди ја сочинуваат светлосната класа III.

Останати подрачја

Меѓу главната низа и низата на џиновски ѕвезди се наоѓаат ретките подџинови со светлосната класа IV. Нивниот пречник е подолг од ѕвездите од главната низа а пократок од ѕвездите од низата на џинови.

Околу густо заземената главна низа и низата на џинови сместено е подрачјето на сјајни џинови со светлосна класа II како и хиперџиновите со светлосна класа I. Овие подрачја се потесни, но рамномерно поплнети.

Под главната низа се наоѓа подрачјето на џуџиња со величина околу 1–3 помалку од ѕвездите во главната низа. Како изолирано подрачје во ѕвездената класификација од B до G е групата на бели џуџиња со величина околу 8–12 помала од ѕвездите во главната низа и многу помал пречник.

Објаснување

Многу од ѕвездите го заземаат подрачјето на дијаграмот наречено главна низа. За време на таа фаза, ѕвездите соединуваат водород во нивните јадра. Следната концентрација на ѕвезди е на хоризонталната линија (хелиумско соединување во јадрото и горење на водородот околу кората на јадрото). Друго важно подрачје е Херцшпрунговата празнина, сместена во подрачјето меѓу ѕвездените видови A5 и G0 и меѓу +1 и −3 апсолутна величина (меѓу врвот на главната низа и џиновите на хоризонталната линија). RR Lyrae може да се најдат лево од јазот. Кефеидите се сместени во горниот дел од секцијата на несигурна линија.

Херцшпрунг-Раселовиот дијаграм може да се користи од страна на научниците и да се измери оддалеченоста на ѕвезденото јато од Земјата. Ова може да се направи со споредба на јасни величина на ѕвезди во јатото до апсолутната величина на ѕвезди со позната оддалеченост (моделни ѕвезди). Откриената група, тогаш се поместува во вертикалната насока, додека главните две низи не вкрстат. Разликата во величината, којашто беше преместена за да дојде до вкрстување на двете групи се нарекува апсолутна величина и е непосредно измерена за оддалеченоста. Оваа техника е позната како приспособување на главната низа, или збунувачки спектроскопски паралакс.

Значење

Концентрацијата на ѕвезди во различните груи позволува да се објасни теоријата на ѕвездена евлуција. Развојот на ѕвездите повеќе или помалку јасно се граничи и наоѓа на одредени места на Х-Р дијаграмот. Со текот на времето се менуваат и делотворната температура на ѕвездите и нејзината мгнитуда во зависност од јадреното соединување во нивната внатрешност, па така секоја ѕвезда својот животен век го поминува низ Х-Р дијаграмот. Ова се одвива со различна брзина. Развојните процеси кои траат подолго, според почесто се набљудуваат (на пр. во главната низа) како побрзи во однос на пократките развои (на пр. во подрачјкето на Херцшпрунговиот јаз). Од другата страна, во Херцшпрунг-Раселовиот дијаграм повеќе нема ѕвезда со делотворна температура околу 3000−5000 келвини, бидејќи овде се наоѓа подрачјето на протоѕвезди, кои имаат долг развоен период. Оваа речиси вертикална линија е позната како патека Хајаши.

Таму ѕвездените типови се поврзани со температурата. ХР-дијаграмот може да се нарече и температурновеличински дијаграм.

Наместо за класификација на ѕвездите, бојниот показател на ѕвездите може да послужи како мерка за нејзината температура. Ако не се познава оддалеченоста на ѕвездата или ѕвезденото јато, тогаш може привидната величина да се искористи, како клучен фактор за одредување на апсолутната величина. Наместо Херцшпрунг-Раселов дијаграм, тоа се нарекува обоенвеличински дијаграм. И двата дијаграма еден по друг верно ја прикажуваат оддалеченоста на ѕвезденото јато.

Улогата на дијаграмот во развојот на ѕвездената физика

Изучувањето на дијаграмот ги водело астрономите до шпекулациите дека тој можеби претставува ѕвезден развој, главно убедување според кое ѕвездите од црвени џинови стануваат кафеави џуџиња, поместувајќи се надолу по линијата од главната низа, во движење на нивниот животен век. И покрај тоа, следната Раселова презентација на дијаграмот на средбата со Кралското астрономско друштво во 1912, Артур Едингтон бил инспириран да го искористи како снова за развивање на идеите на ѕвездената физика (Портер, 2003). Во 1936, во неговата книга Внатрешен состав на ѕвездите, тој со помош на физиката објаснува како ѕвездите се распоредени во дијаграмот. Ова бил еден навистина значаен развој, бидејќи во тоа време големиот проблем на ѕвездената теорија, изворот на ѕвездената енергија не бил решен. Термојадрената енргија, па дури и дека ѕвездите во најголем делсодржат водород (видете металичност) сѐ уште треба да бидат откриени. Едингтон водел до пренасочување на овој проблем во термодинамиката на радиоактивниот пренос на енергија во внатрешноста на ѕвездите (Смит, 1995). Едингтон предвидел дека ѕвездите џуџиња остануваат во суштински неподвижна позиција во главната низа за најголем дел од нивните животи. Во 1930-тите и 1940-тите, со сфаќање на соединувањето на водородот, се појавила теоријата за развој на ѕвездите до црвени џинови и бели џуџиња, која во основа е заснована врз физиката. Од ова време, проучувањата на Херцшпрунг-Раселовиот дијаграм не доведуваат до такви развивања, но едиствено дозволуваат ѕвездениот развој да биде графички претставен.

Поврзано

Наводи

↑ За точна година се смета и 1913, но најчесто се зема предвид 1910. http://sk.pandapedia.com/wiki/Hertzsprungov-Russellov_diagram Архивирано на 5 март 2016 г.
↑ „Информатор за љубителите на астрономијата“, четврто идание, 1971, стр.131-132, Едиториал УРСС (ISBN 5-8360-0303-3)

Наводи

Casagrande, L.; Portinari, L., and Flynn, C. (2006). „Accurate fundamental parameters for lower main-sequence stars“ (Извадок). MNRAS. 373 (1): 13–44. doi:10.1111/j.1365-2966.2006.10999.x.CS1-одржување: повеќе имиња: список на автори (link)
Porter, Roy (2003). The Cambridge History of Science. Cambridge, UK: Cambridge University Press. стр. 518. ISBN 978-0521572439.
Sekiguchi, Maki; Fukugita, Masataka (2000). „A Study of the B-V Color-Temperature Relation“ (HTML). The Astronomical Journal. 120 (2): 1072–1084. doi:10.1086/301490.
Smith, Robert (1995). Observational Astrophysics. Cambridge, UK: Cambridge University Press. стр. 236. ISBN 978-0521278348.

Надворешни врски

JavaHRD Херцшпрунг-Раселовиот дијаграм како Јава апликација
BaSTI вреќа од ѕвездени патеки и изохрони, симулации со кодот FRANEC од астрономската опсерваторија Терамо
Леос Одра: Првиот Херцшпрунг-Раселов дијаграм

[1] За точна година се смета и 1913, но најчесто се зема предвид 1910. http://sk.pandapedia.com/wiki/Hertzsprungov-Russellov_diagram Архивирано на 5 март 2016 г.

[2] „Информатор за љубителите на астрономијата“, четврто идание, 1971, стр.131-132, Едиториал УРСС (ISBN 5-8360-0303-3)

[1]

[2]