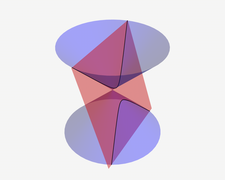
Конусен пресек

Конусен пресек – пресек на конус и произволна рамнина во просторот. Конусните пресеци заземаат многу значајно место како во геометријата, така и во целата математика. Постојат различни видови на пресеци. Се делат на дегенерирани (точка, права или две прави кои се сечат), и недегенерирани (криви). Недегенерираните се пресеци кај кои рамнината не го содржи темето на конусот и таквите пресеци се нарекуваат коники или коници. Тука спаѓаат параболата, хиперболата, елипсата, како и специјалниот случај на елипса – кружницата. Основна одлика на недегенирираните конусни пресеци (освен кружницата) е дека постои точка (фокус) и права (директриса) такви што односот на растојанието на произволна точка од кониката до нив е константен. Во аналитичката геометрија, кониката може да се дефинира како рамнинска алгебарска крива од втор ред. Кониките се многу битни за многу области. На пример, во астрономијата: небесните тела се движат по патеки кои се коники, во оптиката (конструкција на леќи и огледала), во механиката и многу други области. Често се применува и во палеонтологијата за разбирање на изгледот на одредени организми.

Елипса
Кружница
Хипербола
Парабола

Историја на конусните пресеци[уреди | уреди извор]

Стара Грција[уреди | уреди извор]

Проучувањето на конусните пресеци датира уште од античко време. Се смета дека конусните пресеци прв ги открил, дефинирал и опишал Менехмус (Menaechmus, околу 375-325 година пр.н.е.), ученик на Платон и тутор на Александар Македонски. Работата на Менехмус не е сочувана, така што денес за неа дознаваме само до различни списи на негови современици. Конусните пресеци ги користел при обидите за решавање на три проблеми на конструктивната геометрија: квадратура на круг, трисекција на агол и удвојување на коцка. Дефиницијата која тогаш се користела се разликува од денешната. Дури кога во XIX век било докажано дека наведените три проблеми не се решливи со употреба само на линијар и шестар, конусните пресеци почнале да се дефинираат како пресеци на исправен кружен конус и рамнина. Во Стара Грција конусите ги конструирале со вртење на правоаголен триаголник околу една катета, така што хипотенузата ја генерира површината на конусот. Одредувањето на кониката се вршело така што се посматрал аголот меѓу рамнината и темениот агол (двократна големина на аголот кој го образуваат хипотенузата и катетата околу која се ротира триаголникот). Ако аголот е остар, кониката е елипса, ако е прав, парабола, и ако аголот е тап, се работи за хипербола.

Се смета дека со конусни пресеци се занимавал и Евклид (околу 3390275 година пр.н.е.), меѓутоа ни неговите трудови не се сочувани. Кониките, со посебен акцент на параболата, ги проучувал и Архимед (297-212 година пр.н.е.). Неговите трудови како „Расправи за квадратурата на парабола“ се сочувани до денес.

Во проучувањето на кониките посебен придонес дал Аполониј (околу 262-190 година пр.н.е.), математичар и астроном. Тој ја напишал монографијата „Конусни пресеци“ која се состоела од осум книги со 787 става. Првите четири книги се на старогрчки јазик, наредните три на персиски, додека осмата, последната, е изгубена. Аполониј прв ги дал основните теории за сите три коники на кружен, исправен или кос конус, за што пишувал во првата книга. Исто така, прв ги воочил двете гранки на хиперболата, за што, покрај цртањето на тангентите на хиперболата и изучување на нејзините асимптоти, пишувал во втората книга.

Во третата книга се занимавал со одредени теореми за површините и хармониските својства на половите на кониките. Четвртата книга била продолжение на третата, додека во петтата, шестата и седмата се опишани негови сопствени откритија. Како најоригинална од сите се смета петтата книга во која се разгледува нормалата како максимална и минимална права линија повлечена од точка на кривата. Во шестата книга се зборува за поклопувањето и сличноста на конусите, а во седмата книга се зборува за пречниците и праволиниските фигури опишани над тие пречници. Аполониј прв ги дал имињата: парабола, хипербола и елипса. Иако не му бил познат алгебарскиот начин на претставување на конките, многу Аполониеви резултати можат непосредно да се запишат со методот на координати. Тој се смета за еден од најголемите математичари во историјата кои се занимавале со геометрија и најголем во Стара Грција, покрај Евклид.

Последен антички великан на геометријата кој ги проучувал конусните пресеци бил Пап (290-350 година н.е.) од Александрија. Во своето дело „Колекција“, покрај тоа што ги обединил сознанијата од своите претходници, ги вовел поимите фокус и директриса на хипербола.

Конусни пресеци во арапскиот свет[уреди | уреди извор]

Персискиот математичар, физичар и астроном Ал-Кухи во X век направил инструмент за цртање конусни пресеци. Инструментот бил наречен конусен шестар. Користејќи ги кониките, поточно пресек на две параболи, Ал-Кухи го решил проблемот на конструкција на рамностран петаголник впишан во зададен квадрат. Друг персиски математичар Омар Ал-Хајам (1048-1131) кој исто така бил и астроном, филозоф, поет и полиглот, ги превел Аполониевите дела на арапски јазик. Тоа биле петтата, шестата и седмата книга од Аполониевието дело „Конусни пресеци“. Исто така, ја користел параболата и (правоаголната) хипербола при решавање на кубни равенки.

Европа[уреди | уреди извор]

Во Европа научниците не се занимавале со кониките сè до ренесансата. Прв значаен чекор биле Кеплеровите закони (Јохан Кеплер, 1571—1630, германски астроном). Кеплеровите закони се три теории кои ги поставил тој. Првиот Кеплеров закон е најбитен за продолжување на изучувањето на кониките и зборува за тоа дека телата во Сончевиот Систем се движат околу Сонцето по коника, а Сонцето се наоѓа во фокусот на таа коника. Тој разликувал пет вида коники, за разлика од Аполониј кој разликувал само три вида. Кониките кои ги разликувал Кеплер се кружница, елипса, парабола, хипербола и права. Се смета дека прв во Европа ги вовел називите „фокус“ и „директриса“ во 1604 година (прв ги вовел Пап во врска со хиперболата). Се смета дека тврдел дека со поместување на фокусите на една коника може да се добие друга (од елипса може да се добие кружница преку приближување на фокусите и нивно совпаѓање, додека со оддалечување на фокусите може да се добие парабола). Прв почнал да го изучува законот на континуитет. Врз основа на Кеплеровите трудови, Лајбниц (Готфрид Вилхелм Лајбниц) подоцна продолжил да ги изучува кониките.

Проучувањето на кониките особено било забрзано со настанувањето на проективната геометрија чии втемелувачи биле Дезарг (Жерар Дезарг, 1591—1661), Де ла Ир (Филип де ла Ир, 1640—1718) и Паскал (Блез Паскал, 1623—1662). Едно од најпознатите Паскалови дела е „Теорема за мистичниот хексаграм“ во која се наоѓа и доказот на теоремата:„Ако во коника е впишан хексаграмот (шестаголникот) 1231'2'3', тогаш пресеците на трите пара спротивни страни 12' со 1'2, 23' со 2'3 и 13'со 1'3 се колинеарни“.

Декарт (Рене Декарт, 1596—1650) заедно со Ферма (Пјер де Ферма, 1601—1665) ги поставил темелите на денешната аналитичка геометрија. Волис (Џон Волис, 1616—1703) прв, во 1655 година ги дефинирал кониките како геометриски репрезентации на равенки од втор степен. Сепак, можеби најголемо значење на кониките и конусните пресеци им дал Њутн (Исак Њутн, 1642—1727) со откритието дека орбитите на небесните тела се коники, односно со докажување на Кеплеровите закони. Денес, кружните запченици ги движат машините; знаеме за параболични антени и фарови на автомобили; цистерните и ехо локаторите ги користат особините на хиперболата. Со еден збор кажано, кониките се насекаде околу нас.

Особини на конусните пресеци[уреди | уреди извор]

За сите коники, освен кружницата, важи дека постои точка $F$ која се нарекува фокус на кониката, и права $d$ која се нарекува директриса такви што односот на растојанието на произволна точка $M$ од кониката до фокусот $F$ ' и директрисата $d$ е константен.

 $e={\frac {MF}{d(M,d)}}$

Тој однос се нарекува ексцентритет на кониката и се означува со $e$ . Ако ексцентритетот е број меѓу 0 и 1, кониката е елипса, а во специјален случај, кога ексцентритетот е еднаков на 0, кониката е кружница. Параболата има ексцентритет 1, додека кониката чиј ексцентритет е поголем од 1 е хипербола.

Теорема. Секоја коника, освен кружницата, е геометриско место од точки во рамнината за кои односот на растојанието од некоја точка $F$ (фокусот) и некоја постојана права $d$ (директриса) е константна величина.

Фокусот на кружницата воедно е и негов центар, а директриса е бесконечно далечната права.

Елипсата и хиперболата имаат два фокуса и соодветни директриси.

Параболата има само еден фокус и една директриса.

Уште една особина заедничка за сите коники, освен параболата, е линеарниот ексцентритет. Линеарниот ексцентритет претставува оддалеченост на центарот на кониката до нејзиниот фокус, или еден од фокусите. Најчесто се означува со $c$ .

Тетивата која поминува низ фокусот или еден од двата фокуса на кониката и е паралелна со директристата се нарекува latus rectum. Фокусниот параметар на кониката е растојанието меѓу фокусот, или еден од фокусите на кониката, и директрисата. Се означува со $p$ .

коника	канонична равенка	ексцентрицитет ( $e$ )	линеарен ексцентрицитет ( $c$ )	latus rectum ( $l$ )	фокусен параметар ( $p$ )
кружница	${x^{2}}+{y^{2}}=r^{2},\ r>0$	$0$	$0$	$r$	$\infty$
елипса	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,\ a>b>0$	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {{a^{2}}-{b^{2}}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {{a^{2}}-{b^{2}}}}}$
парабола	$y^{2}=2px,\ p>0$	$1$	$-$	$2a$	$2a$
хипербола	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\ a,b>0$	${\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {{a^{2}}+{b^{2}}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {{a^{2}}+{b^{2}}}}}$

Конструкција[уреди | уреди извор]

Трите основни конусни пресеци се елипса, парабола и хипербола. Кружница може да се третира како четврта коника, или како специјален случај на елипса. Кружницата и елипсата се добиваат кога пресекот на кружниот конус со рамнина е затворена крива. Кружницата се добива кога рамнината која го сече конусот е поставена паралелно на рамнината во која лежи кружницата на конусот – кога е во прашање прав конус како на сликата горе на страната, пресечната рамнина е нормална на оската на симетрија на конусот. Ако пресечната рамнина е паралелна на точно една права која генерира конус, добиениот конусен пресек не е ограничен и се нарекува парабола. Во преостанатиот случај, кога рамнината ги сече двете компоненти на конусот, се добиваат две раздвоени неограничени криви кои се нарекуваат гранки на хипербола.

Канонски облик[уреди | уреди извор]

Во Декартови координати равенките на кониките може да се запишат во својот канонски облик:^[1]

Кружница: $x^{2}+y^{2}=r^{2}\,$
Елипса: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1$
Парабола: $y^{2}=2px$
Хипербола: ${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1,\;{x^{2} \over b^{2}}-{y^{2} \over a^{2}}=-1$

Параболата поседува својство на оскина симетрија, додека кружницата, елипсата и хиперболата се централно симетрични.

Конусните пресеци може да бидат зададени и со своите параметарски равенки:

Кружница: $(x=x_{0}+rcos\theta ,\ y=y_{0}+rsin\theta ),\qquad \theta \in [0,2\pi )$ ,
Елипса: $(x=x_{0}+acos\theta ,\ y=y_{0}+bsin\theta ),\qquad \theta \in [0,2\pi )$ ,
Парабола: $(x=x_{0}+{\frac {t^{2}}{2p}},\ y=y_{0}+t),\qquad t\in R$ ,
Хипербола: $x=x_{0}\pm a\cosh \theta ,\ y=y_{0}+b\sinh \theta ),\qquad \theta \in R$ .

Декартов координатен систем[уреди | уреди извор]

Во Декартовиот координатен систем, графиконот на квадратна функција со две непознати $f(x,y)$ може да биде конусен пресек.

Равенката на конусни пресеци е во облик: $f(x,y)\equiv Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ ^[2], каде $A,B,C,D,E$ и $F$ не се сите еднакви на нула.

Бидејќи скалирањето на константите $A,B,C,D,E$ и $F$ не влијае на множеството на нули на функцијата $f(x,y)$ , конусните пресеци може да се посматраат како точки во петодимензионален проективен простор $P^{5}$ .

Класификација според дискриминантата[уреди | уреди извор]

Конусни пресеци дадени со оваа равенка може да се класифицираат според вредноста на Дискриминантата^[3]^[4], $B^{2}-4AC$ .

Ако конусните пресеци не се дегенерирани, тогаш:

ако е $B^{2}-4AC<0$ $B^{2}-4AC<0$ , равенката претставува елипса
- ако е $A=C$ и $B=0$ , равенката претставува кружница, кој е специјален случај на елипса
ако е $B^{2}-4AC=0$ , равенката претставува парабола
ако е $B^{2}-4AC>0$ $B^{2}-4AC>0$ , равенката претставува хипербола
- ако покрај тоа и $A+C=0$ , равенката претставува правоаголна хипербола

Како би ги разликувале дегенерираните случаи од стандардните (недегенерираните), нека $\Delta$ е детерминанта на матрица 3х3:

${\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}$ , тј. $\Delta =(AC-B^{2}/4)F+BED/4-CD^{2}/4-AE^{2}/4$ .

Конусен пресек не е дегенериран ако и само ако е ∆ ≠ 0. Ако је ∆ = 0 во прашање е некој од случаите на дегенерирани конусни пресеци.

Матрична нотација[уреди | уреди извор]

Равенката на конусен пресек може да се напише во матричен облик:

${\begin{bmatrix}x&y\end{bmatrix}}{\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+Dx+Ey+F=0$

Типот на кониката е еднозначно одреден со детерминантата на матрицата во средината на претходната равенка. Ако детерминантата е позитивна, нула или негативна, тогаш во прашање е елипса, парабола или хипербола соодветно. Ако двете својствени вредности на средната матрица се различно од нула (т.е. ако кониката е елипса или хипербола), променливите може да се трансформираат така што се добива:

$\left({\begin{array}{c}x-a\\y-c\end{array}}\right)^{T}\left({\begin{array}{cc}A&{\frac {B}{2}}\\{\frac {B}{2}}&C\end{array}}\right)\left({\begin{array}{c}x-a\\y-c\end{array}}\right)=G$

каде a, c и G ги задоволуваат равенките $D+2aA+Bc=0,E+2Cc+Ba=0$ и $G=Aa^{2}+Cc^{2}+Bac-F$ .

Исто така може да се запише во облик:

${\begin{bmatrix}x&y&1\end{bmatrix}}{\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}=0$ .

Ако детерминантата на средната матрица (3х3) е различна од нула, конусниот пресек не е дегенериран. Ако детерминантата е еднаква на нула, конусниот пресек е дегенерирана парабола (две паралелни прави или две прави кои се поклопуваат), дегенерирана елипса (точка на елипсата), или дегенерирана хипербола (две прави кои се сечат).

Дел од квадратна форма[уреди | уреди извор]

Равенката

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

може да се напише во следниов облик:

$Ax^{2}+Bxy+Cy^{2}=-(Dx+Ey+F)$ .

Значи, кониката може да се претстави како пресек на графикот на квадратната форма $z=Ax^{2}+Bxy+Cy^{2}$ и рамнината $z=-(Dx+Ey+F)$ .

Ексцентрицитет изразен преку параметрите на квадратна форма[уреди | уреди извор]

Кога кониката е запишана алгебарски како:
$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ ,
ексцентрицитетот може да се запише како функција на параметрите на квадратна равенка.^[5] Ако $4AC=B^{2}$ , кониката е парабола и нејзиниот ексцентрицитет е еднаков на 1. Во спротивен случај, земајќи предвид дека равенката претставува хипербола или неимагинарна елипса, ексцентритетот е даден со:

$e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}}$

каде $\eta =1$ ако детерминантата на матрицата 3х3 (од матричната нотација) е негативна, а $\eta =-1$ ако таа детерминанта е позитивна.

Инваријантни коники[уреди | уреди извор]

Трагата и детерминантата на ${\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}$ се инваријанти во однос на ротацијата околу координатните оски и транслацијата на рамнина.^[6]^[7]

Константниот израз $F$ е инваријантен само при ротација.

Изменет облик[уреди | уреди извор]

За некои практични примени корисно е кониката да се претстави во поларен координатен систем, во облик во кој точката на фокусот е поставена во координатниот почеток. Другиот фокус, ако постои, се поставува на негативниот дел (кај елипсата), односно на позитивниот дел на х-оската (кај хиперболата).

Таа равенка го има обликот:

$r={\frac {l}{1-e\cos {\theta }}}$ ,

каде $e$ е ексцентрицитетот, а $l$ е половина од должината на сегментната линија која ги спојува двете точки на кониката и притоа поминува низ фокусот и е паралелна со директрисата (latus rectum):

$l={\frac {b^{2}}{a}}$ , каде $a$ и $b$ се полуоски на кониката.

За $e=0$ имаме кружница, за $0<e<1$ елипса, за $e=1$ парабола и за $e>1$ хипербола.

Поларниот облик на равенката на конусни пресеци често се користи во динамиката, на пример, за одредување на орбитите на објектите кои се движат околу Сонцето.^[8]

Во Декартовиот координатен систем равенката има облик:

${\begin{alignedat}{7}{\sqrt {x^{2}+y^{2}}}=\left(l+ex\right)\ \Rightarrow \ \left({\frac {x-{\frac {le}{1-e^{2}}}}{\frac {l}{1-e^{2}}}}\right)^{2}+{\frac {\left(1-e^{2}\right)y^{2}}{l^{2}}}=1\end{alignedat}}$

Линеарниот ексцентрицитет е даден со:

$c=\left({\frac {le}{1-e^{2}}}\right)$

Различните коники од општите формули може да се претстават во Декартовиот координатен систем на следниов начин:

Кружница: $x^{2}+y^{2}=r^{2}$
Елипса: ${\frac {(x-{\sqrt {a^{2}-b^{2}}})^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
Парабола: $y^{2}=4a(x+a)$
Хипербола: ${\frac {(x+{\sqrt {a^{2}+b^{2}}})^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Пет точки ја одредуваат кониката[уреди | уреди извор]

Пет копланарни точки, меѓу кои никои три не се колинеарни, еднозначно ја одредуваат кониката. Ако меѓу петте точки има три или повеќе колинеарни точки, тие исто така одредуваат конусен пресек, кој е еден од трите дегенерирани случаи.

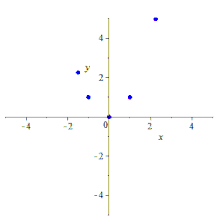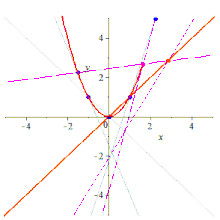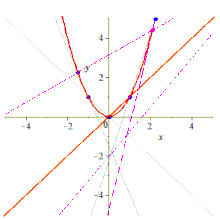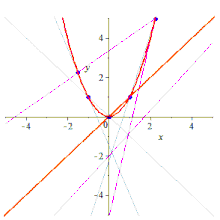
Дегенерирани конусни пресеци[уреди | уреди извор]

Дегериран случај го сметаме пресекот на рамнина и конус кој го содржи темето на конусот. Може да биде:

точка, кога аголот меѓу рамнината и оската на конусот е поголем од аголот меѓу оската и изводницата на конусот (и помал од 180° – аголот меѓу оската и изводницата на конусот);
права, кога аголот меѓу рамнината и оската на конусот е ист како и аголот меѓу оската и изводницата на конусот;
две прави кои се сечат, кога аголот меѓу рамнината и оската на конусот е помал од аголот меѓу оската и изводницата на конусот.

Точка
Права
Две прави

Коники во другите области[уреди | уреди извор]

Кос истрел[уреди | уреди извор]

Движењето на тело кое се истрелува од висина $h$ , со почетна брзина ${\vec {v}}_{0}$ и под агол $\alpha$ во однос на тлото, таканаречен кос истрел, има патека со облик на парабола. Ако се занемари отпорот на воздухот, освен почетните услови, на телото ќе влијае и гравитациското поле.

Движење на телата во Сончевиот Систем[уреди | уреди извор]

Првиот Кеплеров закон вели дека телата на Сончевиот Систем се движат околу Сонцето по коника во чиј фокус се наоѓа Сонцето. Повеќето планети се движат приближно по кружна патека, затоа што ексцентритетот им е близок до нула (Земјиниот 0,0167, а Јупитеровиот 0,0488). Интересно е дека Халеевата Комета има ексцентрицитет близок до единица (околу 0,995).

Радиоантени (во астрономијата)[уреди | уреди извор]

Радиоантените се засноваат на оптичките својства на кониките. Радиобрановите, заради големата бранова должина, не е едноставно да се детектираат, па заради тоа се користат параболични антени, во чии фокуси се наоѓаат приемниците. Заради големата оддалеченост сите зраци кои паѓаат на површината се приближно паралелни и ќе се одбијат точно во приемникот (фокусот на параболоидот).

Радиоастрономска опсерваторија, Сан Агустин, САД
Одбивање на зраците од рефлектор

Елипсеста маса за билјард[уреди | уреди извор]

Елипсестата маса за билјард ги користи оптичките својства на елипсата. Ако се изведе удар без спин од белата точка, во кој било правец, топката секогаш ќе влезе во дупката. Тоа својство на масата се добива со тоа што точката од која се изведува ударот и дупката се наоѓаат во фокусите на елипсата. Пример на ваква маса може да се види на видео-клипот: Pool Table - Numberphile.^[9]

Наводи[уреди | уреди извор]

↑ Protter & Morrey (1970). pp. 314—328, 585-589
↑ Protter & Morrey (1970, 316. str)
↑ Fanchi, John R. (2006), [1], John Wiley and Sons, pp. 44 i 45
↑ [2]
↑ Ayoub, Ayoub B., "The eccentricity of a conic section," [Ayoub, Ayoub B., "The eccentricity of a conic section,"] 34(2), Mart 2003, 116–121.
↑ Protter & Morrey (1970). pp. 326
↑ Pettofrezzo, Anthony, "Matrices and Transformations", Dover Publ., (1966). pp. 101–111
↑ Brannan, Esplen & Gray 1999, стр. 17.
↑ Elliptical Pool Table - Numberphile

Литература[уреди | уреди извор]

Šukilović, T. Vukmirović, S.(2015), Geometrija za informatičare, Matematički fakultet u BeograduCS1-одржување: повеќе имиња: список на автори (link)
Akopyan, A.V. & Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. ISBN 0-8218-4323-0.
Boyer, Carl B. (2004) [1956]. History of Analytic Geometry. Dover. ISBN 978-0-486-43832-0.
Dixon, A. C. (March 1908), „The Conic through Five Given Points“, The Mathematical Gazette, The Mathematical Association, JSTOR 3605147

Надворешни врски[уреди | уреди извор]

„Конусен пресек“ на Ризницата ^?

Конусни пресеци на mathworld.wolfram.com (англиски)
Изведување на равенките на конусните пресеци (англиски)
Конусни пресеци (англиски)
Појава на коники во природата (англиски)
Конике Архивирано на 6 октомври 2007 г. (англиски)

[1] Protter & Morrey (1970). pp. 314—328, 585-589

[2] Protter & Morrey (1970, 316. str)

[3] Fanchi, John R. (2006), [1], John Wiley and Sons, pp. 44 i 45

[4] [2]

[5] Ayoub, Ayoub B., "The eccentricity of a conic section," [Ayoub, Ayoub B., "The eccentricity of a conic section,"] 34(2), Mart 2003, 116–121.

[6] Protter & Morrey (1970). pp. 326

[7] Pettofrezzo, Anthony, "Matrices and Transformations", Dover Publ., (1966). pp. 101–111

[FOOTNOTEBrannanEsplenGray199917-8] Brannan, Esplen & Gray 1999, стр. 17.

[9] Elliptical Pool Table - Numberphile

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]