Електрична отпорност
Електрична отпорност (или специфична електрична отпорност) е мера во која еден материјал дава отпор (се противи) на текот на електрична струја. Ниска отпорност значи дека материјалот без проблем дозволува течење на електрично полнење низ него. SI единица за електричен отпор е ом метар.
Дефиниции[уреди | уреди извор]
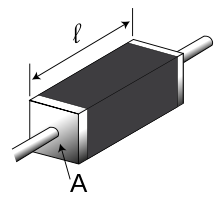
Електричната отпорност ρ („ро“) на еден материјал зависи од
каде
- ρ е статичната отпорност (изразена во ом метри - Ωm)
- R е електричната отпорност на еднообразен примерок на материјал (изразена во омови - Ω)
- l е должината на примерокот (изразена во метри - m)
- A е пресекот на примерокот (изразен во квадратни метри - m²)
Електричната отпорност може да се дефинира и како
каде
- E е величината на електричното поле (изразена во волти на метар - V/m)
- J е величината на густината на струјата (изразена во ампери на квадратен метар A/m²)
Најпосле, електричната отпорност се дефинира и како обратна на спроводливоста σ (сигма), на материјалот, или
Таблица на отпорности[уреди | уреди извор]
На оваа таблица се прикажани отпорноста и температурниот коефициент на разни материјали. Вредностите се точни на 20 °C
| Материјал | Отпорност (Ωm) | Температурен коефициент во келвини * |
|---|---|---|
| Сребро[1] | 1,47 × 10−8 | ,0038 |
| Бакар[1] | 1,72 × 10−8 | ,0039 |
| Злато[1] | 2,44 × 10−8 | ,0034 |
| Алуминиум[1] | 2,82 × 10−8 | ,0039 |
| Волфрам[1] | 5,6 × 10−8 | ,0045 |
| Железо[1] | 1,0 × 10−7 | ,005 |
МесингГрешка во наводот: Отворачката ознака <ref> не е добро срочена или има погрешно име. |
0,8 × 10−7 | ,0015 |
| Платина[1] | 1,1 × 10−7 | ,00392 |
| Олово[1] | 2,2 × 10−7 | ,0039 |
| Манганин[2] | 4,4 × 10−7 | ,000002 |
| Константан[2] | 4,9 × 10−7 | ,00001 |
| Жива[2] | 9,8 × 10−7 | ,0009 |
| Нихром[1][3] | 1,10 × 10−6 | ,0004 |
| Јаглерод[1][4] | 3,5 × 10−5 | -,0005 |
| Германиум[1][4] | 4,6 × 10−1 | -,048 |
| Силициум[1][4] | 6,40 × 102 | -,075 |
| Стакло[1] | 1010 до 1014 | нема |
| Тврда гума[1] | околу 1013 | нема |
| Сулфур[1] | 1015 | нема |
| Кварц (фузиран)[1] | 7,5 × 1017 | нема |
| ПЕТ | околу 1 × 1020 | нема |
| Тефлон | околу 1 × 1022 to 1 × 1024 | нема |
- Броевите во оваа колона го зголемуваат или намалуваат мантисниот дел од отпорноста. На пример, при 21 °C (294,15K), отпорноста на среброто изнесува 1,4738 × 10−8
Зависност од температура[уреди | уреди извор]
Воопштено, електричната отпорност на металите се зголемува со температура, додека отпорноста на полуспроводниците се намалува со зголемување на температурата. Во обата случаја содејствувањата на релација електрон-фонон играт клучна улога. При повисоки температури, отпорот на металот се зголемува правопропорционално со температурата. При намалување на истата, температурната зависност на отпорноста следи функција со закон на степенување на таа температура. Математички температурната зависност на отпорноста ρ на еден метал е дадена во Блох-Грунајсеновата формула :
каде е остаточна отпорност заради распрснувањето кое доаѓа од дефектите, A а е константа која зависи од брзината на електроните на Фермиевата површина, Дебајевиот полупречник и густината на бројот на електроните во металот. е Дебјева температура според мерењата на отпорност и е речиси иста со вредностите на Дебјевата температура добиени со мерењата на специфичната температура. n е цел број кој зависи од карактерот на содејствувањата:
- n=5 имплицира дека отпорот се должи на распрснувањето на електрони од страна на фононите (како што е за простите метали)
- n=3 имплицира дека отпорот се должи на s-d расопсрнување на електрони (како што е со преодните метали)
- n=2 имплицира дека отпорот се должи на содејствувањето на релација електрон-електрон.
Со доволно намалување на температурата на металот (така што сите фонони се 'замрзнуваат'), отпорноста достигнува постојана вредност, позната како остаточна отпорност. Оваа вредност не зависи само од видот на метал, туку и од неговата чистота и топлинска историја. Вредноста на остаточната отпорност на еден материјал се одредува преку концентрацијата на примеси. Некои материјали ја губат сета електрична отпорност при доволно ниски температури, заради ефектот наречен суперспроводливост.
Еве уште подобра претстава за отпороноста на еден полуспроводник со помош на Штајнхарт-Хартовата равенка:
каде A, B и C се т.н. Штајнхарт-Хартови коефициенти.
Равенкава се користи за баждарење на термистори.
Комплексна отпорност[уреди | уреди извор]
При анализирање на реакциите на материјалот при променливи електрични полиња, како што се прави кај извесни видови томографија, потребно е отпорноста да се замени со комплексна величина наречена импеданција, аналогно на електричната импеданса. Импендансата е збир на реалната компонента, отпорноста, и имагарна компонента, реактивноста (реактанса) [1] Архивирано на 13 октомври 2010 г..
Извори[уреди | уреди извор]
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 Serway, Raymond A. (1998). Principles of Physics (2 изд.. изд.). Fort Worth, Texas; London: Saunders College Pub. стр. стр. 602. ISBN 0-03-020457-7.
- ↑ 2,0 2,1 2,2 Giancoli, Douglas C. (1995). Physics: principles with applications (4 изд.. изд.). London: Prentice Hall. ISBN 0-13-102153-2.
(видете и Таблица на отпорност (англиски)) - ↑ Ni,Fe,Cr - легура за грејни тела.
- ↑ 4,0 4,1 4,2 Отпорноста на полуспроводниците во голема мера зависи од примесите во материјалот.
- Paul Tipler (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5 изд.). W. H. Freeman. ISBN 0-7167-0810-8.







