Античестичка
| Антиматерија |
|---|
 |
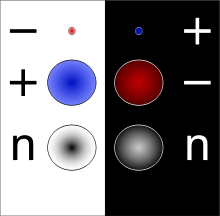
Античестичка — антиматериски двојник на некоја честичка со иста маса и спротивен полнеж. На пример, античестичката на електронот е позитивно наелектризираниот позитрон кој се добива природно во некои видови на радиоактивно распаѓање. Природните закони се речиси симетрични за античестичките и честичките. На пример, антипротон и позитрон можат да формираат антиводороден атом, за кој се верува дека има исти својства како и водородниот атом. Ова довело до прашањето зошто формацијата на материја по големата експлозија резултирало во вселена која се состои речиси целосно од материја, а не мешавина од материја и антиматерија. Подоцна се открило дека симетријата не е совршена, туку приближна. Паровите честичка-античестичка меѓусебно се поништуваат, при што се ослободуваат фотони. На пример позитроните произведени во природен радиоактивен распад многу брзо се поништуваат со електрони при што ослободуваат гама-зраци. Античестичките природно се произведуваат при бета-распадот и во заемодејството на космичко зрачење во Земјината атмосфера. Бидејќи полнежот се зачувува, не е возможно да се создаде античестичка без да се уништи честичка со ист полнеж, или да се создаде и честичка со спротивен полнеж. Иако античестичките и честичките имаат спротивни полнежи, електро неутралните честички не мора да се идентични со своите античестички. Неутронот е изграден од кваркови, а антинеутронот од антикваркови, меѓу кои може да се прави разлика бидејќи при контакт, меѓусебно се поништуваат. Но некои неутрални честички, самите си се свои античестички, како фотонот и гравитонот.
Историја[уреди | уреди извор]
Опит[уреди | уреди извор]
Во 1932, бргу откако Пол Дирак го предвидел постоењето на позитронот, Карл Дејвид Андерсон открил дека судир на космичко зрачење може да ги произведе овие честички во Вилсонова Комора – детектор на честички во кој електрони (или позитрони) во движење можат да се откријат по трагата која ја оставаат кога се движат низ гас. Односот на електричниот полнеж наспроти масата на честичката може да се измери така што се набљудува полупречникот на виткање на патеката во магнетно поле. За позитроните, поради правецот на кој се виткаат нивните патишта, најпрвин се мислело дека се електрони кои се движат во спротивна насока. Антипротонот и антинеутронот биле откриени од Емилио Сегре и Овен Чемберлејн во 1955 во Калифорнискиот универзитет во Беркли. Оттогаш биле создадени повеќе античестички во забрзувачи на честички. Во последните години дури биле и создадени целосни атоми од антиматерија, зачувани во електромагнетни стапици.[1]
Теорема за Дираковата дупка[уреди | уреди извор]
... развојот на квантната теорија за полето го направила непотребно разбирањето за античестички како дупки, иако тоа се задржува во повеќе учебници.
Решенија на Дираковата равенка содржеле негативни енергетски квантни состојби. Како резултат на тоа, електрон би можел секогаш да зрачи енергија и да премине во состојба на негативна енергија. Уште полошо, би можел да зрачи бесконечни количества на енергија, бидејќи постоеле бесконечно многу негативни енергетски состојби. За да не се случи оваа нефизичка ситуација, Дирак предложил „море“ од електрони со негативна енергија која ја исполнува вселената, кои веќе ги окупираат сите можни пониско-енергетски состојби, така да ниеден друг електрон не може да премине во таква состојба. (поради принципот на Паули за исклучок). Понекогаш некоја од овие негативно-енергични честички би можела да се движи надвор од ова Дираково море за да стане позитивно-енергична честичка. Но во тој случај би оставила „дупка“ во морето која би се однесувала како позитивно-енергичен електрон со спротивен полнеж. Овие тој ги разбрал како „електрони со негативна енергија“ и се обидел да ги идентификува со протон во неговиот труд „Теорија за Електрони и Протони“ во 1930г. [3] Меѓутоа, се покажало дека овие „електрони со негтивна енергија„ се позитрони, а не протони.
Ова укажувало на бесконечен негативен полнеж на вселената – проблем за кој Дирак бил свесен. Тој се обидел да објасни дека тоа треба да го разбереме како нормална состојба на нула полнеж. Друга тешкотија била разликата во масата на електронот и протонот. Дирак се обидувал да објасни дека ова е поради електромагнетните заемодејства со „морето„, сè додека Херман Вејл не докажал дека теоријата на дупка е целосно симетрична кај негативните и позитивните полнежи. Дирак исто така предвидел реакција
e−
+
p+
→
γ
+
γ
, каде електрон и протон се поништуваат за да се добијат два фотона. Роберт Опенхајмер и Игор Там докажале дека ова би предизвикало да обичната материја исчезнува пребрзо. Една година подоцна, во 1931, Дирак ја изменил својата теорија и ја открил честичката позитрон – нова честичка со иста маса како електронот. Откритието на оваа честичка следната година ги побило противречностите во неговата теорија
Но сепак останува проблемот на бесконечниот полнеж на вселената. Исто така, сега знаеме дека бозоните исто така имаат античестички, но бидејќи бозоните не го следат принципот за исклучок на Паули (само фермионите го прават тоа) теоријата за дупка не важи за нив. Унифицираното толкување на античестичките е присутно и во квантната теорија за полето, која ги решава овие два проблема.
Заемно поништување на честичка и античестичка[уреди | уреди извор]

Ако честичка и античестичка се во приближни квантни состојби, можат меѓусебно да се поништат и да произведат други честички. Реакции како
e−
+
e+
→
γ
+
γ
(поништување на електрон и позитрон) се пример за тоа. Реакција на поништување на електрон и позитрон при што се добива еден фотон ,
e−
+
e+
→
γ
не е возможна во слободен простор бидејќи е невозможно да се зачуваат енергијата и инерцијата заедно во процесот. Но во Коуломбово поле, јадрото на пресликувачката инваријанца е прекршен и е можна такво поништување
[4] Спротивната реакција(во слободен простор без атомско јадро) е исто така невозможна поради истата причина. Во квантната теорија за полето, овој процес е дозволен како интермедиерна квантна состојба за време доволно кратко за прекршокот на зачувувањето на енергијата да може да се занемари со принципот на несигурност. Поради ова можно е производство на виртуелен пар или негово поништување во која една честичка се движи меѓу две состојби и назад. Овие процеси се важни за вакуум состојбата и ренормализацијата на теоријата на квантно поле. Исто така отвора можност за неутрална честичка да се измеша со сличен процес – сложен пример за ренормализација на масата.
Својства на античестичките[уреди | уреди извор]
Квантните состојби на честичка и античестичка можат да се менуваат со примена на оператори како конјугација на полнеж (C), парност (P) и T-симетрија (T). Ако ја покажува квантната состојба на честичка (n) со моментум p, спин J чија компонента во z-правецот е σ, тогаш
Каде nc ја покажува состојбата на конјургиран полнеж – античестичката. Ова однесување подCPT е исто како тврдењето дека честичката и нејзината античестичка лежат во иста несмаллива репрезентација на Поанкареова група. Својствата на античестичка се споредливи со тие на честичките со ова. Ако T е добра симетрија на динамиката тогаш
Каде знакот за пропорционалност покажува дека може да има фаза на десната страна. Со други зборови, честичка и античестичка мора да имаат
- иста маса m
- иста состојба на спин J
- спротивни електрични полнежиq and -q.
Теорија на квантно поле[уреди | уреди извор]
Електронско поле може да се квантува без мешање на операторите на поништувањето и создавање така што
Каде симболот „k“ го покажува квантиот број p и σ на претходниот дел и знакот за енергијата, E(k), и akго покажува соодветниот оператор за поништување. Се разбира, бидејќи работиме со фермиони, операторите мора да задоволуваат канонични односи и односи на антикомутативност. Но ако се запише Хамилтоновата
тогаш веднаш се гледа дека очекуваната вредност на „H“ не мора да е позитивна. Ова е поради тоа што E(k) може да има каков било знак и комбинацијата на оператори на создавање и поништување има очекувана вредност 1 или 0. Затоа мора да се воведе конјургираното поле на античестички со свои оператори и записи
Каде k има исто p, и спротивно σ и знак за енергија.Тогаш полето може да се запише како
Каде првата сума е над позитивните енергетски состојби а втората е над тие со негативна енергија. Енергијата станува
Каде E0 е бесконечна негативна константа. Состојбата на вакуум е дефинирана како состојба без честичка или античестичка - и . Тогаш енергијата од вакуумот е еднаква на E0. Бидејќи сите енергии се мерат во однос на вакуумот, H е позитивен. Анализа на својствата на ak и bk покажува дека еден оператор е за поништување на честички а другиот за античестички. Овој случај е кај фермионот. Ова е заслуга на Владимир Фок, Вендел Фури и Роберт Опенхајмер. Ако се квантува реално скаларно поле, тогаш постои само еден оператор за поништување, така да, реални скаларни полиња опишуваат неутрални бозони. Бидејќи комплексните скаларни полиња покажуваат два вида на оператори за поништување, кои се поврзани со конјугација, такви полиња опишуваат бозони со полнеж.
Фајнман–Штукелбергово толкување[уреди | уреди извор]
Така што се зема предвид растењето на модулот на негативна енергија на електронско поле наназад во времето, Ернст Штукелберг сликовито увидел дека честичката и античестичката имаат еднаква маса и спин, но спротивен полнеж. Ова му дозволило да ја запише тероријата на пертубација со прецизни дијаграми. Фајнман подоцна дал независно системско изведување на овие дијаграми од формализмот на честичките, кои се наречени Фајнманови дијаграми. Секоја линија на дијаграмот претставува честичка која се движи нанапред или наназад во времето. Оваа техника е најпознат метод за пресметување на амплитуди во квантната теориај за полето. Бидејќи оваа слика прво била развиена од Ернст Штукелберг, а Фајнман ја разработил, е наречено Фајнман–Штукелберг толкување во чест на двајцата научници. Последица од сето ова било, Вилата образложил дека претпоставката дека антиматеријата е CPT-трансформирана материја би имплицирала дека гравитациското заемодејство меѓу материјата и антиматеријата е одбивно.[5]
Поврзано[уреди | уреди извор]
- Гравитациско заемојдество на антиматеријата
- Парност (физика) и Конјугација на полнеж
- Квантна теорија за полето и список на честички
- Бариогенеза
Наводи[уреди | уреди извор]
| „Античестичка“ на Ризницата ? |
- ↑ http://news.nationalgeographic.com/news/2010/11/101118-antimatter-trapped-engines-bombs-nature-science-cern/
- ↑ Weinberg, Steve. The quantum theory of fields, Volume 1 : Foundations. стр. 14. ISBN 0-521-55001-7.
- ↑ Dirac, Paul (1930). „A Theory of Electrons and Protons“. Proceedings of the Royal Society A. 126 (801): 360–365. Bibcode:1930RSPSA.126..360D. doi:10.1098/rspa.1930.0013.
- ↑ Sodickson, L.; W. Bowman; J. Stephenson (1961). „Single-Quantum Annihilation of Positrons“. Physical Review. 124 (6): 1851–1861. Bibcode:1961PhRv..124.1851S. doi:10.1103/PhysRev.124.1851.
- ↑ M. Villata, CPT symmetry and antimatter gravity in general relativity, 2011, EPL (Europhysics Letters) 94, 20001
- Feynman, R. P. (1987). „The reason for antiparticles“. Во R. P. Feynman and S. Weinberg (уред.). The 1986 Dirac memorial lectures. Cambridge University Press. ISBN 0-521-34000-4.
- Weinberg, S. (1995). The Quantum Theory of Fields, Volume 1: Foundations. Cambridge University Press. ISBN 0-521-55001-7.
|












