Јунгов модул

Јунгов модул
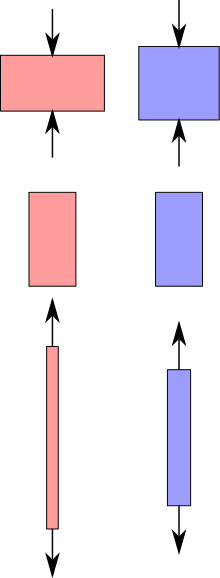Приказ на даден едноосен напор, без оглед дали е издолжувачки или збивачки создава деформација во материјало со мала тврдост (црвено) а по тоа е со висока тврдост (сино). Јунговиот модул служои за мерење на таа тврдост.
Симболи	E, Y
SI-единица	Pa
Во основни единици	Pa = kg m−1 s−2
Димензија	M L−1 T−2
Изведенки од други величини	$E\equiv {\frac {\sigma (\varepsilon )}{\varepsilon }}={\frac {F/A}{\Delta L/L_{0}}}={\frac {FL_{0}}{A\Delta L}}$

Јунгов модул е механичко својство кое ја мери вкочанетоста на цврст материјал. Го дефинира односот помеѓу напон (сила по единица површина) и напрегнатост (пропорционална деформација) во материјал во линеарна еластичност режим на едноосна деформација.

Јунговиот модул е именуван по Британскиот научник Томас Јунг од 19 век. Сепак, концептот е развиен во 1727 година од Леонард Ојлер, а првите експерименти, кои го користат замислата на Јунгов модул во сегашниот облик биле изведени од италијанскиот научник Џордано рикати во 1782 година, што е за 25 години пред Јунговата работа. Терминот модул потекнува од латинскиот поим modus што значи мерка.

Дефиниција

Линеарна еластичност

Главна статија: Линиска еластичност

Цврст материјал ќе има еластична деформација кога ќе му се закачи мал товар при збивање или издолжување. Еластичната деформација е повратна (материјалот се враќа во неговата првичен облик откако ќе се отстрани товарот).

Во близина на нула напор и напрегање, кривата на напон-напрегање е линеарна, и врската помеѓу напон и напрегањето е опишана од страна на Хуковиот закон кој наведува дека напорот е пропорционален на притисокот. Коефициентот на пропорционалност е Јунговиот модул. Колку е поголем модулот, толку повеќе напон е потребно да се постигне исто напрегање; идеално цврсто тело би имало бесконечен Јунгов модул.

Не многу материјали се линеарни и еластични по мало деформирање.

Формула и единици

$E={\frac {\sigma }{\epsilon }}$, каде

• ${\displaystyle }$ е еднооскен напон, или еднооскна сила по единица површина, во
• ${\displaystyle }$ е притисок, или пропорционална деформација (промена во должината поделена со оригиналната должина) (адимензионален)

Во пракса, Јунгов модул е даден во мегапаскали (MPa или N/mm²) или гигапаскали (GPa или kN/mm²).

Не треба да се меша со

Материјална вкочанетост не треба да се меша со:

• Сила: максималната количина на притисок што материјалот може да издржи останувајќи во еластичниот (реверзибилен) деформационен режим;
• Геометриска вкочанетост: глобална одлика на телото кое зависи од својата форма, и не само на локална сопственост на материјалот; на пример, I зрак има повисока свиткана вкочанетост од прачка на истиот материјал за дадена маса по должина;
• Цврстина: односот на отпорот на материјалната површината на пенетрација од страна на потешко телото;
• Грубост: износот на енергија која материјал може да апсорбира пред прекршување.

Употреба

Јунгов модул овозможува пресметка на промените во димензија на бар направен од изотропски еластичен материјал под затегнувачки или компресивни товари. На пример, се предвидува колку материјал примерок се протега под тензија или се скратува под компресија. Јунгов модул директно се однесува на случаите на еднооскен напон, кој е затегнувачки или компресивен напон во една насока и без напон во други насоки. Јунгов модул исто така се користи со цел да се предвидат девијации што ќе се случат во статично одреден зрак кога товар е применет во една точка помеѓу каде зрак е поддржуван. Други еластични пресметки обично бараат употреба на една дополнително еластична сопственост, како што се модул на смолкнување, модул на збивливост или односот na Poisson. Било кои два од овие параметри се доволни за целосно да ja опишaт еластичноста во изотропичен материјал.

Линеарни наспроти не-линеарни

Јунгов модул претставува фактор на пропорционалност во Хуков закон, кој се однесува на напон и напрегнатост. Сепак, законот на Хук е валиден само при еластичен и линеарен одглас. Било кој друг вистински материјал на крајот нема да успее и ќе се прекрши кога  ќе се протегне преку многу голема далечина или со многу голема сила; сепак сите цврсти материјали покажуваат речиси Хуково однесување за доволно мали видови напор или напрегнатост. Ако опсегот над кој Хуков закон е валиден е доволно голем, во споредба со типичниот притисок на кој се очекува да биде нанесен на материјалот, материјалот се вели дека е линеарен. Во спротивно (ако типичен стрес би се применувало надвор од линеарен опсег) материјалот се вели дека ќе биде не-линеарен.

Челик, јаглеродни влакна и стакло, меѓу други обично се сметаат за линеарни материјали, додека други материјали како гума и почви се не-линеарни. Сепак, ова не е апсолутна класификација: ако многу мал напор или притисок се нанесени на не-линеарен материјал, тогаш реакцијата ќе биде линеарна, но ако многу висок притисок или напор се нанесени на линеарен материјал, линеарната теорија нема да биде доволно. На пример, како што линеарната теорија подразбира реверзибилност, тогаш би било апсурдно да се користи линеарна теорија да се опише неуспехот на челичен мост под висок товар; иако челик е линеарен материјал за повеќето апликации, тоа не е во таков случај на катастрофален неуспех.

Во солидна механика, наклонот на напон-напрегнатост кривина во било која точка се нарекува тангентен модул. Тоа може да биде експериментално утврдено од наклонот на притисок–напон кривина создадена во текот на затегнувачка тестови спроведени на примерок од материјалот.

Насочни материјали

Јунгов модул не е секогаш ист во сите ориентации на материјалот. Повеќето метали и керамика, заедно со многу други материјали, се изотропски, и нивните механички одлики се исти во сите ориентации. Сепак, метали и керамика, може да се третираат со одредени нечисти, и метали може да биде механички изработени да ги направат своите зрнести структури насочени. Овие материјали потоа стануваат анизотропни, и Јунгов модул ќе се промени во зависност од насоката на силата на векторот. Анизотропи може да се видат во многу композити. На пример, јаглеродни влакна имаат многу повисок Јунгов модул (многу поцврст) кога сила е натоварена паралелно со влакна ( заедно со зрно). Други такви материјали вклучуваат дрво и армиран бетон. Инженери може да го користат овој дирекционен феномен во нивна предност во создавање на структури.

Пресметка

${\displaystyle }$${\displaystyle }$${\displaystyle }$Јунгов модул E, може да се пресметува со делење на затегнувачкиот стрес, , од инженерска екстензија на напон, во еластичен (почетен, линеарен) дел на физички притисок–напон искривување каде

E е Јунгов модул (модул на еластичност)

F е силата нанесена на некој предмет под тензија;

А е вистинската пресечна област, која е еднаква на областа на пресекот нормално на применетата сила;

ΔL е износот на должината на објектот што се променува (ΔL е позитивен ако материјалот е протегала , и негативни, кога материјалот е компримиран);

L₀ е оригиналната должината на предметот.

Сила извршена од протегнат или стеснат материјал

${\displaystyle }$Јунговиот модул на материјал може да се користи за да се пресмета силата што ја врши под специфична напрегнатост.

каде F е на сила притискан од материјалот кога договорената или се протегала од ΔL.${\displaystyle }$Законот на Хук за протегната жица може да се изведе со оваа формула:${\displaystyle }$ ${\displaystyle }$од каде таа доаѓа во заситеност и

Но, имајте на ум дека еластичноста на извиткани федери доаѓа од модул на смолкнување, не Јунгов модул.

Еластична потенцијална енергија

Еластична потенцијална енергија складирана во линеарен еластичен материјал е дадена од страна на составниот дел на Хуков закон:

${\displaystyle }$

сега со појаснување на интензивните променливи:

${\displaystyle }$

Ова значи дека еластичната потенцијална енергија густина (односно, по единица волумен) е дадена со:

${\displaystyle }$

или, во едноставни нотации, за еден линеарен еластичен материјал: ${\displaystyle }$бидејќи напрегнатоста е дефинирана ${\displaystyle }$.

Во не-линеарен еластичен материјал Јунгов модул е функција на напрегнатост, па втората еквивалентност веќе не важи и еластичната енергија не е квадратна функција на напрегнатоста:

${\displaystyle }$

Однос меѓу еластични константи

За homogeneous isotropic материјали едноставни односи постојат меѓу еластични константи (Јунгов модул E, модул на смолкнување G, модул на збивливост К, и Поисонов коефициент ν) кои овозможуваат пресметување на сите нив додека две се познати:

${\displaystyle }$

Приближни вредности

Влијанија на одбрани стакло компоненти дополнувања на Јунгов модул на одредена база на стакло

Јунгов модул може да се разликува малку поради разликите во примерниот состав и тест метод. Брзината на деформација има најголемо влијание на собраните податоци, особено во полимери. Вредностите тука се приближни и само со цел за релативната споредба.

Приближен унгов модул за различни материјали

Материјал	GPa	Mpsi
Гума (мала напрегнатост)	0.01–0.1	1.45–6998145000000000000♠14.5×10−3
Полиетилен со ниска густина	0.11–0.86	1.6–6998650000000000000♠6.5×10−2
Дијатоми фрустули (главно силициумска киселина)	0.35–2.77	0.05–0.4
PTFE (Тефлон)	0.5	0.075
HDPE	0.8	0.116
Бактериофаги капсиди	1–3	0.15–0.435
Полипропилен	1.5–2	0.22–0.29
Поликарбонат	2–2.4	0.29-0.36
Полиетилен терефталат (ПЕТ)	2–2.7	0.29–0.39
Најлон	2–4	0.29–0.58
Полистирен, солиден	3–3.5	0.44–0.51
Полистирен, пена	0.0025–0.007	0.00036–0.00102
масло од дрво со средна густина	4	0.58
дрво (со скроб)	11	1.60
Човечка компактна коска	14	2.03
Полиестерска матрица зајакната со стакло	17.2	2.49
Ароматични пептидни наноцевки	19–27	2.76–3.92
Високo цврст бетон	30	4.35
Аминокиселински молекуларни кристали	21–44	3.04–6.38
Од јаглеродни влакна зајакната пластика (50/50 влакна / матрица, биаксијална ткаенина)	30–50	4.35–7.25
Конопско влакно	35	5.08
Магнезиум метал(Mg)	45	6.53
СтаклоПредлошка:Specify	50–90	7.25–13.1
Ленски влакна	58	8.41
Aлуминиум	69	10
Седеф	70	10.2
Арамид	70.5–112.4	10.2–16.3
Глеѓ (претежно калциум фосфат)	83	12
влакно од коприва	87	12.6
Бронза	96–120	13.9–17.4
Месинг	100–125	14.5–18.1
Титан (Ti)	110.3	16
Титански легури	105–120	15–17.5
Бакар (Cu)	117	17
Од јаглеродни влакна зајакната пластика (70/30 влакна / матрица, еднонасочно, заедно со влакното)	181	26.3
Силициум монокристал, различно насочно	130–185	18.9–26.8
Ковано железо	190–210	27.6–30.5
Челик (ASTM-A36)	200	29
поликристален железен гранат од иттриум (YIG)	193	28
монокристален итриум железо кобалт (YIG)	200	29
Кобалт-Хром (CoCr)	220–258	29
Ароматични пептидни наносфери	230–275	33.4–40
Берилиум (Be)	287	41.6
Молибден (Mo)	329–330	47.7–47.9
Волфрам (W)	400–410	58–59
Силициум карбид (SiC)	450	65
Карбид волфрам (WC)	450–650	65–94
Осмиум (Os)	525–562	76.1–81.5
Еднослојна јаглеродна наноцевка	1,000+	150+
Графен (C)	1050	152
Дијамант (C)	1050–1210	152–175
Карбин (C)	32100	7007321000000000000♠4,660

Поврзано

• Свиткување вкочанетост
• Девијации
• Деформација
• Flexural modulus
• Хуков закон
• Импулс побудување техника
• Список на материјали својства
• Принос (инженерство)

Дополнителна литература

• ASTM E 111, "Стандардна Тест Метода за Јунгов модул, Tangent Modulus, и Орда Modulus"
• На ASM Handbook (разни тома) содржи Јунгов модул за различни материјали и информации за пресметки. Онлајн верзија (бара претплата)(бара претплата)

Надворешни врски

• Matweb: бесплатна база на податоци за инженерски особини на повеќе од 115.000 материјали
• Млад е Modulus за групи на материјали, и нивната цена