Паралелограм
| Паралелограм | |
|---|---|
 Во паралелограм спротивните страни се исти | |
| Вид | Четириаголник |
| Рабови и темиња | 4 |
| Група на симетрија | C2 |
| Плоштина | a·h |
| Обем | 2a+2b |
| Својства | испакнат |
Во геометријата, паралелограм е четириаголник со два пара паралелни страни.
- Основна регулатива: Еден паралелограм е потполно определен со должините на две соседни страни и големината на аголот помеѓу нив.
| Четириаголник е паралелограм ако и само ако спротивните страни се исти (складни).[1] |
Овој факт се користи при стандардно означување на четирите типови паралелограми.[2][3]
- Ромбоид: паралелограм каде што соседните страни не се со еднаква должина и нема внатрешен прав агол.
- Ромб: паралелограм каде што четирите страни се со еднаква должина.
- Правоаголник: паралелограм каде што четирите внатрешни агли се прави, т.е. по 90°.
- Квадрат: паралелограм каде што четирите страни се со еднаква должина и четирите агли се прави, т.е. по 90°.

|

|

|

|
| Ромбоид | Ромб | Правоаголник | Квадрат |
Формули и особини за паралелограм[уреди | уреди извор]
- Едниот пар на паралелни страни се „земаат“ за основи и (обично) се означуваат со a. Вообичаено е да се земат хоризонталните (или најхоризонталните или најдолгите) страни за основи. Честопати се користи зборот должина.
- Другиот пар на паралелни страни се викаат краци и (обично) се означуваат со b.
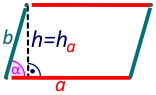
- Растојанието помеѓу основите се вика висина и (обично) се означува со h (или ha за да се разликува од другата висина hb меѓу краците). Растојанието помеѓу краците исто така е висина на паралелограмот, но во однос на краците, па затоа специјално се означува со hb.
Нека е даден паралелограм со основа a, крак b, висина h (меѓу основите) и агол α помеѓу а и b.
 Висина h меѓу основите |
Периметар
Плоштина е: должина по висина односно основа по висина[4]
| . Попрецизно: и |
- Плоштина на еден паралелограм се одредува со основа и висина. Меѓутоа, само со тие информации, паралелограм не е еднозначно определен, односно постојат безброј многу различни паралелограми со иста основа и висина. Истите ја имаат истата плоштина, а различни периметри.[5]
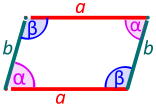
- Бидејќи секоја страна на паралелограм е и трансверзала на другите паралелните страни, според Претпоставката за паралелност секој пар соседни внатрешни агли се суплементни, т.е. нивниот збир е 180°.[2]
- Бидејќи секој паралелограм е четириаголник, збирот на внатрешните агли е 360°.
- Од суплементност на соседни агли следува дека спротивните агли се исти (складни).
- Секоја дијагонала е и трансверзала, па го дели паралелограмот на два складни триаголници. Следува дека двата пара паралелни страни се складни (со иста должина).[1]
- Пресечната точка на дијагоналите е средината на двете дијагонали. Со други зборови,
| Дијагоналите на паралелограм се преполовуваат.[6] |
Висина
- и
Дијагонали (каде што дијагоналата d1 минува низ аголот α)
- и [7]
Пример: Нека е даден паралелограм со основа a=5 km, и крак b=3 km и агол α=30° помеѓу a и b. Тогаш, периметарот e L=2a+2b=16 km, висина е h=b·sin(α)=1,5 km и плоштината е P=ah=7,5 км2.
Пример: Нека е даден паралелограм со основа a=5 km, и крак b=2.5 km и агол α=37° помеѓу a и b. Тогаш, периметарот e L=2a+2b=15 km, висина е h=b·sin(α)≈1,5 km и плоштината е P=ah≈7,5 км2.
Одлики на паралелограм[уреди | уреди извор]
испакнат четириаголник е паралелограм ако и само ако кој било од следните искази е вистинит[8][9]
- Двата пара на спротивни страни се еднакво долги.
- Двата пара на спротивни агли се со еднаква големина.
- Дијагоналите се сечат во нивните средни точки.
- Еден пар на спротивни страни се паралелни и се еднакво долги.
- Соседните агли се суплементни.
- Секоја дијагонала го дели четириаголникот на два складни триаголници.
- Збирот на квадратите на страните е еднаков на збирот на квадратите на дијагоналите (закон на паралелограм).
Впишана и опишана кружница на паралелограм[уреди | уреди извор]
- Паралелограм нема впишана кружница освен ако е ромб (или квадрат).[10]
- Паралелограм нема опишана кружница освен ако е правоаголник (или квадрат).[9]
Симетрија[уреди | уреди извор]
Осна симетрија[уреди | уреди извор]
Види ги поединечните типови на паралелограми.
Вртежна симетрија[уреди | уреди извор]
При ротација на паралелограм 360°/2=180° се добива истиот паралелограм.
- Ромбоидот, ромбот и правоаголникот имаат вртежна симетрија од 2-ри ред (180°).
- Квадратот има вртежна симетрија од 4-ти ред (90°).
Обопштување на паралелограм[уреди | уреди извор]
- Обопштување во 3Д: Паралелопипед е полиедар со 6 страни, секоја од нив е паралелограм.
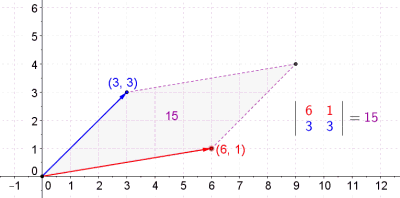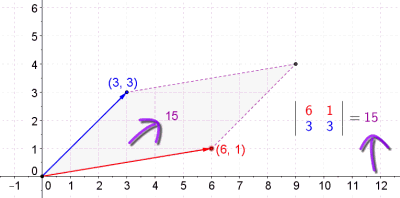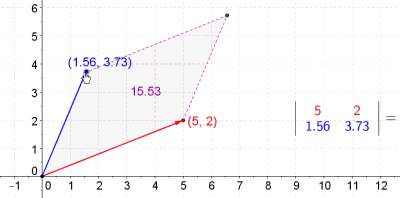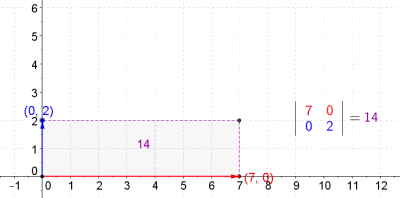 Пресметување плоштина на паралелограм со детерминанта |
Паралелограми и вектори, матрици, детерминанти[уреди | уреди извор]
- Еден паралелограм е потполно определен со два вектора со истата почетна точка. (Четвртата точка е крајната точка на збирот на векторите.)
Во линеарната алгебра, апсолутната вредност на детерминантата на 2х2 матрица A е плоштината на паралелограмот формиран со соодветните полупречник-вектори.
- Соодветните полупречник-вектори се
- Соодветните темиња на паралелограмот се
- Плоштината Р на паралелограмот со темиња A, B, C, D e (апсолутната вредност на)
Доколку имаме паралелограм ABCD каде што А≠(0,0), формираме складен паралелограм EFGH со транслација -А така што Е=А-А=(0,0), F=B-A, G=C-A и H=D-A. Потоа со детерминанта се пресметува плоштината на EFGH која е иста со плоштината на паралелограмот ABCD (плоштините на складни 2-димензионални геометриски фигури се исти).
Ова својство се обопштува до 3-димензии, односно за волумен на паралелопипед преку мешан производ како и во повисоки димензии.
Поврзани теми[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ 1,0 1,1 Kleyn, I. „Спротивните страни на паралелограм се еднакви“ (англиски). algebra.com. Посетено на 1 септември 2013.
- ↑ 2,0 2,1 C.Clapham, J.Nicholson (2009). „Oxford Concise Dictionary of Mathematics“ (PDF) (англиски). Addison-Wesley. стр. 581–582. Посетено на 1 септември 2013.
- ↑ „Паралелограм“ (англиски). Math Open Reference. 2009. Посетено на 1 септември 2013. интерактивен
- ↑ Боривоје Миладиновиќ, Трајче Ѓорѓијевски и Никола Петрески, Математика за II година гимназиско образование. Скопје: Алби, 2009, стр. 119.
- ↑ Стојановска, Л. (2010). „Паралелограм“. Архивирано од изворникот на 2013-09-15. Посетено на 1 септември 2013. интерактивен
- ↑ Kleyn, I. „Одлики на дијагоналите на паралелограм“ (англиски). algebra.com. Посетено на 1 септември 2013.
- ↑ Kleyn, I. „Должина на дијагонали користејќи ја [[косинусова теорема]]“ (англиски). algebra.com. Посетено на 1 септември 2013. URL–wikilink conflict (help)
- ↑ Byer, Owen; Lazebnik, Felix; Smeltzer, Deirdre (2010). Methods for Euclidean Geometry. Mathematical Association of America. стр. 51–52.
- ↑ 9,0 9,1 Usiskin, Zalman; Griffin, Jennifer; Witonsky, David; Willmore, Edwin (2008), http://books.google.com/books?id=ZkoUR5lRwdcC&pg=PA63 На
|chapterurl=му недостасува наслов (help), The Classification of Quadrilaterals: A Study of Definition, 10. Cyclic quadrilaterals, Research in mathematics education, IAP, стр. 22, ISBN 978-1-59311-695-8 - ↑ Andreescu, Titu; Enescu, Bogdan (2006). Mathematical Olympiad Treasures. Birkhäuser. стр. 64–68. ISBN 978-0817682521..
Надворешни врски[уреди | уреди извор]
- Стојановска, Л. (2010). „Паралелограм“. Архивирано од изворникот на 2013-09-15. Посетено на 1 септември 2013. интерактивен
- Стојановска, Л.; Тромпеска, М. (2010). „Конструкција на паралелограм со две страни и агол]“. Посетено на 1 септември 2013. интерактивен со видео објаснување за рачна и Геогебра конструкција
- Стојановска, Л.; Тромпеска, М. (2010). „Конструкција на паралелограм со две страни и висина“. Посетено на 1 септември 2013. интерактивен со видео објаснување за рачна и Геогебра конструкција
- Стојановска, Л.; Тромпеска, М. (2010). „Конструкција на паралелограм со две страни и дијагонала“. Посетено на 1 септември 2013. интерактивен со видео објаснување за рачна и Геогебра конструкција
- Златковска, С. (2012). „Мини презентација за дијагонали и висини на паралелограм“. Архивирано од изворникот на 2016-03-05. Посетено на 1 септември 2013.
- R. Pierce (2011). „Вртежна симетрија“ (англиски). MathisFun. Посетено на 1 септември 2013.
- „Паралелограм“ (англиски). Math Open Reference. 2009. Посетено на 1 септември 2013. интерактивен
- „Плоштина на паралелограм“ (англиски). Math Open Reference. 2009. Посетено на 1 септември 2013. интерактивен
- „Дијагонали на паралелограм“ (англиски). Math Open Reference. 2009. Посетено на 1 септември 2013. интерактивен
- {{Наведена мрежна страница | url=http://www.elsy.at/kurse/index.php?kurs=Parallelogram+and+Rhombus&status=public Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)] (англиски)
- Weisstein, Eric W. (2013). „Паралелограм“ (англиски). Math World- A Wolfram Web Resource. Посетено на 1 септември 2013.
- „Interactive Parallelogram --sides, angles and slope“ (англиски). Посетено на 1 септември 2013.
- Bogomolny, A. (2010). „Area of Parallelogram“ (англиски). Cut-the-Knot. Посетено на 1 септември 2013. интерактивен
- Bogomolny, A. (2010). „Equilateral Triangles On Sides of a Parallelogram“ (англиски). Cut-the-Knot. Посетено на 1 септември 2013. интерактивен















![{\displaystyle {A}=\left[{\begin{array}{*{20}{c}}{a_{11}}&{a_{12}}\\{a_{21}}&{a_{22}}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f46968e34fa98cb5912b51972460a1e5a0db097)


