Бијекција

|
| Бијекција. Има точно една стрелка до секој елемент во кодоменот B (од елемент од доменот А). |
Во математиката, бијективна функција или бијекција е функција f : A → B која е и инјективна и сурјективна. Тоа значи: за секој елемент b во кодоменот B постои точно еден елемент a од доменот A таков што f(a)=b. Бијекцијата исто така се нарекува 1-1 кореспонденција.[1][2]
Терминот бијективност и сродните термини сурјективност и инјективност беа воведени од страна на Никола Бурбаки (Nicholas Bourbaki)[3] и група други, воглавно француски математичари од 20 век, кој почнувајќи од 1935 година напиша серија книги за презентирање на модерната напредна математика.
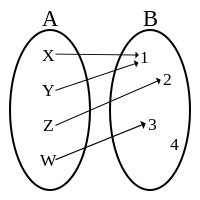
|
| Не е бијекција. (Не е ниту сурјекција, ниту инјекција.) |
Основни својства[уреди | уреди извор]
Формално имаме:
- е бијективна функција ако за секој постои точно еден таков што
Елементот се вика претслика на елементот .
- Функција е бијекција ако и само ако секој елемент во кодоменот има точно една претслика во доменот. (Види и: Сурјективна функција, Инјективна функција.)
Забелешка: Сурјекција значи минимум една претслика. Инјекција значи максимум една претслика. Бијекција значи точно една претслика.
Кардиналност[уреди | уреди извор]
Кардиналноста на едно множество е мерка на бројот на елементите во множеството. На пример, ако A={X,Y,Z,W}, тогаш кардиналноста на А е 4 и пишуваме #A=4. Кардиналноста на едно множество се одредува преку бијекција помеѓу даденото множество и множество со позната кардиналност.[4]
- Две множества ја имаат истата кардиналност ако постои бијекција помеѓу нив. (Види кардиналност.)
- Ако кардиналноста на A и B е конечен број, #A=#B=n тогаш при доказ дека функцијата f:A → B e бијекција доволно е да се докаже дека е сурјекција или да се докаже дека е инјекција.
- Ако кардиналноста на A и B е еднаква, но не е конечен број тогаш ова не важи.
Пример: Нека А=B=ℕ. Идентичната функција f(x)=x e бијекција. Функцијата f(x)=2x е инјекција која не е сурјекција. Функцијата f(x)=round(x/2) е сурјекција која не е инјекција каде што round(z) го заокружува z така што f(1)=round(1/2)=round(0,5)=1, f(2)=round(2/2)=1, f(3)=round(3/2)=round(1,5)=2, ....
Бијекции и инверзни функции[уреди | уреди извор]
- Бијекцијата може да се преврти со обратно насочување на сите стрелки од пресликувањето. Новата функција се вика инверзна функција (на првобитната функција). Види инверзна функција.
Формално: Нека f : A → B е бијективна функција. Инверзната функција на бијективна функција f е (бијективна) функција g : B → A дефинирана со: ако f(a)=b, тогаш g(b)=a. Значи, сите стрелки на пресликување се обратно насочени.
- Инверзна функција на инверзна функција е првобитната функција.[5])
- Една функција има инверзна функција ако и само ако е бијекција.[6][7][8]
Забелешка: Нотацијата за инверзна функција на функцијата f е проблематична. Имено, со
- се означува инверзната функција на функцијата f, а со
- се означува реципрочната вредност на бројот x.
- Една од најважните особини на бијективните функции е тоа дека инверзна релација на бијективна функција е функција, т.н. инверзна функција. Инверзните функции како што се квадратен корен на квадратна функција, логаритамска функција на експоненцијална функција, ... имаат многу голема улога во математиката.
Примери[уреди | уреди извор]
Елементарни функции[уреди | уреди извор]
Нека f(x):ℝ→ℝ е реална функција y од реален аргумент x. (Значи влез и излез се броеви.)
- Графичко толкување: функцијата f е бијекција ако секоја хоризонтала права го пресекува графиконот на f во точно една точка.
- Алгебарско толкување: функцијата f е бијекција ако за кој било yo постои xo таков што yo=f(xo) и ако f(xo)=f(x1) значи xo=x1.
Пример: Линеарната функција на која било коса права е бијективна, односно y=ax+b каде што a≠0 е бијекција. (Види линеарна функција.) Слика 1.
- Дискусија: Види го соодветниот пример кај сурјекција и инјекција.
- Инверзна функција: y=(x-b)/a
Пример: Кубната полиномна функција f(x)=x3 е бијекција. Слика 2 и Слика 5: тенката жолта крива.
- Инверзна функција е 3-ти корен, односно
f(x)= ∛x. Слика 5: дебелата зелена крива.
Пример: Квадратната функција f(x) = x2 не е бијекција (од ℝ→ℝ). Слика 3. Не е сурјекција. Не е инјекција. Меѓутоа со ограничување на доменот и кодоменот до множеството на ненегативни броеви [0,+∞) се добива бијекција (види примери подолу).
Бијекции и нивните инверзни функции[уреди | уреди извор]
Нека f(x):A→B каде што A и B се подмножества на ℝ.
- Да претпоставиме дека f не е бијекција. За кое било x каде што изводот на f постои и не е нула, постои број δ>0 таков да ограничувањето на f на δ-околината на x е бијекцијата (на сликата на околината).[4]
- Графиконите на меѓусебно инверзни функции се симетрични во однос на правата y=x. (Види и Инверзна функција.)
Пример: Квадратната функција дефинирана на ограничениот домен и кодомен [0,+∞)
- каде што
е бијекција. Слика 6: тенката жолта крива.
Пример: Функцијата квадратен корен дефинирана на ограничуваниот домен и кодомен [0,+∞)
- каде што
е бијекцијата дефинирана како инверзната функција на квадратната функција: x2. Слика 6: дебелата зелена крива.
Забелешка: Последниот пример го покажува следното. За одредување дали некоја функција е бијекција или не, потребно е да се знае:
- доменот на функцијата
- машината на функцијата
- кодоменот на функцијата
Пример: Нека машината биде f(x)=x².
- Оваа машина со домен=ℝ и кодомен=ℝ не е инјекција и не е сурјекција. Меѓутоа,
- оваа иста машина со домен=[0,+∞) и кодомен=[0,+∞) е и инјекција и сурјекција, па затоа и бијекција.
Пример: Експоненцијалната функција дефинирана на доменот ℝ и на ограничуваниот кодомен (0,+∞)
- каде што
е бијекција. Слика 4: тенката жолта крива (земено е a=10).
Пример: Логаритамската функција со основа a дефинирана на ограничуваниот домен (0,+∞) и на кодоменот ℝ
- каде што
е бијекцијата дефинирана како инверзната функција на експоненцијалната функција: ax. Слика 4: дебелата зелена крива (земено е a=10).
Наводи[уреди | уреди извор]
- ↑ Weisstein, Eric. „Bijective function“ (англиски). From MathWorld--A Wolfram Web Resource. Посетено на 1 January 2014.[мртва врска]
- ↑ C.Clapham, J.Nicholson (2009). „Oxford Concise Dictionary of Mathematics, Bijection“ (PDF) (англиски). Addison-Wesley. стр. 88. Посетено на 1 January 2014.
- ↑ Miller, Jeff (2010). „Earliest Uses of Some of the Words of Mathematics“ (англиски). Tripod. Посетено на 1 February 2014.
|contribution=е занемарено (help) - ↑ 4,0 4,1 Tanton, James (2005). Encyclopedia of Mathematics, Cardinality. Facts on File, New York. стр. 60. ISBN 0-8160-5124-0. (англиски)
- ↑ „Inverse of Bijection is Bijection“ (англиски). Посетено на 1 February 2014.
- ↑ „Injection iff Left Inverse“ (англиски). Посетено на 1 February 2014.
- ↑ „Surjection iff Right Inverse“ (англиски). Посетено на 1 February 2014.
- ↑ „Bijection iff Left and Right Inverse“ (англиски). Посетено на 1 February 2014.
Поврзано[уреди | уреди извор]
Надворешни врски[уреди | уреди извор]
- „Injective, Surjective, Bijective“ (англиски). 2013. Посетено на 1 декември 2013. интерактивен квиз
- „Injectivity, Surjectivity“ (англиски). Wolfram Alpha. Посетено на 1 декември 2013.[мртва врска] интерактивно





















