Прстен (геометрија)

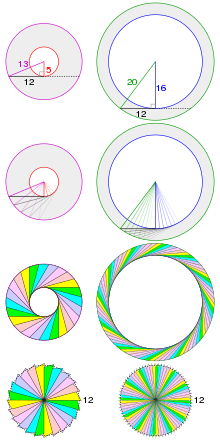
Прстен — во математиката, област помеѓу два концентрични кругови. Овој лик името го добил според неговиот облик на прстен.

Отворениот прстен е тополошки еквивалентен и на отворениот цилиндар $S 1 \times (0,1)$ и на прободена рамнина.

Плоштина[уреди | уреди извор]

Плоштината на прстенот е разлика на плоштините на поголемата кружница со полупречник $R$ и помалата со полупречник $r$ :

A=\pi \left(R^{2}-r^{2}\right)=\pi d^{2}.

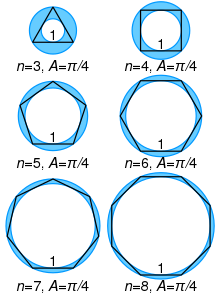
Плоштината на прстенот се определува со должината на најдолгата отсечка во прстенот, што е тангентна тетива на внатрешната кружница, $2 d$ на придружениот дијаграм. Тоа може да се покаже со помош на Питагоровата теорема бидејќи оваа права е тангента на помалата кружница и е нормална на неговиот полупречник во таа точка, така што $d$ и $r$ се страни на правоаголен триаголник со хипотенуза $R$ , а плоштината на прстенот е дадена со:

A=\int _{r}^{R}\!\!2\pi \rho \,d\rho =\pi \left(R^{2}-r^{2}\right).

Плоштината може да се добие и преку пресметка со делење на прстенот на бесконечен број на прстени со бесконечно мала ширина $dρ$ и површина $2π ρ dρ$ и потоа интегрирање од $ρ = r$ до $ρ = R$ :

A={\frac {\theta }{2}}\left(R^{2}-r^{2}\right).

Плоштината на прстенест исечок со агол $θ$ , со $θ$ мерен во радијани, е дадена со:

A=\pi R^{2}-\pi r^{2}=\pi \left(R^{2}-r^{2}\right).

Комплексна структура[уреди | уреди извор]

Во комплексната анализа, прстен $ann(a; r, R)$ во комплексната рамнина е отворен регион дефиниран како:

r<|z-a|<R.

Ако $r$ е $0$ , областа е позната како прободен диск (диск со точка дупка во средиштето) со полупречник $R$ околу точката $a$ .

Како подмножество на сложената рамнина, прстенот може да се смета како Риманова површина. Комплексната структура на прстенот зависи само од соодносот $r R$ .