Кружници на Аполониј

Кружници на Аполониј се кои било од неколкуте групи кружници поврзани со Аполониј од Перга, познат древен геометар. Повеќето од овие кружници се среќаваат во рамнинската Евклидова геометрија, но аналози се дефинирани и на други површини; на пример, соодветните фигури на површината на сферата може да се дефинираат преку стереографска проекција.

Главните употреби на овој термин се петкратни:

1. Аполониј покажал дека кружницата може да се дефинира како множество од точки во рамнина за кои односот на растојанијата до две фиксни точки, познати како фокуси, е константен. Оваа Аполониева кружница е основата на проблемот со потерата на Аполониј. Тоа е посебен случај на првото семејство опишано во #2.
2. Аполониевите кружници се две фамилии на меѓусебно ортогонални кружници. Првата фамилија се состои од кружници за кои се добиваат сите можни соодноси на растојанијата до два фиксни фокуса (истите кружници како во #1), додека второто семејство се состои од сите можни кружници кои минуваат низ двата фокуса. Овие кружници ја формираат основата на биполарните координати .
3. Кружниците на Аполониј на триаголник се три кружници од кои секоја поминува низ едно теме на триаголникот и има константен однос на растојанијата до другите две темиња. Изодинамичните точки и правата на Лемуан на триаголник може да се одредат со помош на овие кружници на Аполониј.
4. Проблемот на Аполониј е да се конструираат кружници кои се истовремено тангентни на три дадени кружници. Решенијата на овој проблем понекогаш се нарекуваат кружници на Аполониј.
5. Аполониевата мрежа (заптивка) е еден од првите фрактали кои некогаш биле опишани. Таа е збир на меѓусебно тангентни кружници, формирани со повторување на проблемот на Аполониј.

Дефиниција за кружница на Аполониј

Слика 1. Дефиниција за кружница на Аполониј.

Кружница обично се дефинира како множество од точки P кои се на дадено фиксно растојание $r$ (радиус на кружницата) од дадена точка (центарот на кружницата). Сепак, постојат и други, еквивалентни дефиниции за кружница. Аполониј открил дека кружницата може да се дефинира како множество од точки P за кои односот на нивните растојанија $\lambda ={\dfrac {d_{1}}{d_{2}}}$ до две дадени точки (означени со A и B на сликата 1) е константен. Овие две точки понекогаш се нарекуваат фокуси.

Доказ со употреба на вектори во Евклидови простори

Нека $d_{1}$, $d_{2}$ се два различни позитивни реални броја. Нека C е внатрешната делбена точка на AB во односот $d_{1}:d_{2}$, a D е надворешната делбена точка на AB во истиот однос, $d_{1}:d_{2}$. Имаме

${\overrightarrow {\mathrm {PC} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}},\ {\overrightarrow {\mathrm {PD} }}={\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}.$

Тогаш,

${\begin{aligned}&{\overline {\mathrm {PA} }}:{\overline {\mathrm {PB} }}=d_{1}:d_{2}.\\\Leftrightarrow {}&d_{2}|{\overrightarrow {\mathrm {PA} }}|=d_{1}|{\overrightarrow {\mathrm {PB} }}|.\\\Leftrightarrow {}&d_{2}^{2}|{\overrightarrow {\mathrm {PA} }}|^{2}=d_{1}^{2}|{\overrightarrow {\mathrm {PB} }}|^{2}.\\\Leftrightarrow {}&(d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }})\cdot (d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }})=0.\\\Leftrightarrow {}&{\frac {d_{2}{\overrightarrow {\mathrm {PA} }}+d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}+d_{1}}}\cdot {\frac {d_{2}{\overrightarrow {\mathrm {PA} }}-d_{1}{\overrightarrow {\mathrm {PB} }}}{d_{2}-d_{1}}}=0.\\\Leftrightarrow {}&{\overrightarrow {\mathrm {PC} }}\cdot {\overrightarrow {\mathrm {PD} }}=0.\\\Leftrightarrow {}&{\overrightarrow {\mathrm {PC} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PD} }}={\vec {0}}\vee {\overrightarrow {\mathrm {PC} }}\perp {\overrightarrow {\mathrm {PD} }}.\\\Leftrightarrow {}&\mathrm {P} =\mathrm {C} \vee \mathrm {P} =\mathrm {D} \vee \angle {\mathrm {CPD} }=90^{\circ }.\end{aligned}}$

Според тоа, точката P е на кружницата со дијаметар CD.

Доказ со помош на теоремата за симетрала на агол

Доказ за дефиницијата на кружница на Аполониј

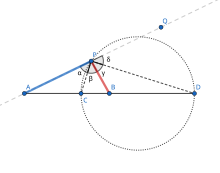
Најпрвин разгледајте ја точката $C$ на отсечката помеѓу $A$ и $B$ која го задоволува соодносот. Од условот

$${\frac {\overline {AP}}{\overline {BP}}}={\frac {\overline {AC}}{\overline {BC}}}$$

па од теоремата за симетрала на агол, аглите $\alpha =\angle APC$ и $\beta =\angle CPB$ се еднакви. Потоа земете ја другата точка $D$ на продолжението на отсечката $AB$ која го задоволува соодносот. Значи

$${\frac {\overline {AP}}{\overline {BP}}}={\frac {\overline {AD}}{\overline {BD}}}.$$

Сега, нека $Q$ е некоја друга точка каде било на продолжението на полуправата $AP$. Според теоремата за симетрала на агол, правата $PD$ го преполовува надворешниот агол $\angle QPB$. Затоа, $\gamma =\angle BPD$ и $\delta =\angle QPD$ се еднакви и $\beta +\gamma =90^{\circ }$. Затоа, според теоремата на Талес, $P$ лежи на кружницата која има дијаметар $CD$.

Проблемот со потера на Аполониј

Проблемот со потера на Аполониј е да се открие дали бродот кој заминува од една точка $A$ со брзина $v_{A}$ може да пресретне друг брод кој ќе тргне од некоја друга точка $B$ и оди со брзина $v_{B}$_. Минималното време на пресретнување на двата брода се пресметува при претпоставка дека бродовите одат праволиниски. Претпоставуваме дека брзините на бродовите не се менуваат, а односот на нивните брзини го означуваме со $\mu$. Ако двата брода се судрат или се сретнат во некоја точка $I$, тогаш растојанијата кои ќе ги помине секој од нив се поврзани со равенката:

$a=\mu b$

Со квадрирање на двете страни, добиваме:

$a^{2}=b^{2}\mu ^{2}$

$a^{2}=x^{2}+y^{2}$

$b^{2}=(d-x)^{2}+y^{2}$

$x^{2}+y^{2}=[(d-x)^{2}+y^{2}]\mu ^{2}$

Ако се развие изразот, имаме:

$x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]\mu ^{2}$

Со понатамошен развој, имаме:

$x^{2}+y^{2}=x^{2}\mu ^{2}+y^{2}\mu ^{2}+d^{2}\mu ^{2}-2dx\mu ^{2}$

Ако се префрлат изразите на левата страна:

$x^{2}-x^{2}\mu ^{2}+y^{2}-y^{2}\mu ^{2}-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

$x^{2}(1-\mu ^{2})+y^{2}(1-\mu ^{2})-d^{2}\mu ^{2}+2dx\mu ^{2}=0$

Изразот се дели со $1-\mu ^{2}$(што е можно бидејќи $\mu \neq 1$):

$x^{2}+y^{2}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+{\frac {2dx\mu ^{2}}{1-\mu ^{2}}}=0$

Го комплетираме изразот до полн квадрат:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}-{\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}-{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}+y^{2}=0$

Ги префрламе не-квадратните членови на десната страна:

${\begin{aligned}\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}\\&={\frac {d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}+{\frac {d^{2}\mu ^{2}}{1-\mu ^{2}}}{\frac {(1-\mu ^{2})}{(1-\mu ^{2})}}\\&={\frac {d^{2}\mu ^{4}+d^{2}\mu ^{2}-d^{2}\mu ^{4}}{(1-\mu ^{2})^{2}}}\\&={\frac {d^{2}\mu ^{2}}{(1-\mu ^{2})^{2}}}\end{aligned}}$

На крајот:

$\left(x+{\frac {d\mu ^{2}}{1-\mu ^{2}}}\right)^{2}+y^{2}=\left({\frac {d\mu }{1-\mu ^{2}}}\right)^{2}$

Затоа, точката мора да лежи на кружница како што е дефинирана од Аполониј, со појдовните точки како фокуси.

Кружници кои имаат заедничка радикална оска

Слика 2. Множество од кружници на Аполониј. Секоја сина кружница ја пресекува секоја црвена кружница под прав агол и обратно. Секоја црвена кружница минува низ двата фокуса, кои одговараат на точките А и B на Слика 1.

Кружниците дефинирани со Аполониевиот проблем за потера за истите две точки A и B, но со различни соодноси на двете брзини, се разделени една од друга и формираат непрекинато семејство кое ја покрива целата рамнина; ова семејство на кружници е познато како хиперболичен прамен. Другото семејство од кружници, кои минуваат низ A и B, се нарекуваат елиптичен прамен. Овие два прамена од Аполониеви кружници се сечат еден со друг под прав агол и ја формираат основата на биполарниот координатен систем. Во секој прамен, кои било две кружници имаат иста радикална оска; радикалните оски на двата прамена се заемно нормални, а центрите на кружниците од едниот прамен лежат на радикалната оска на другиот прамен.

Решенија за проблемот на Аполониј

Проблемот на Аполониј може да има најмногу осум решенија. Трите дадени кружници се обоени во црно, додека кружниците на решението се обоени.

Во Евклидската геометрија на рамнината, проблемот на Аполониј е да се конструираат кружници кои се тангентни на три дадени кружници во рамнината.

За трите дадени кружници генерално има осум различни кружници кои се тангентни на нив и секоја кружница која е решение трите дадени кружници ја допираат на различен начин (однатре или однадвор): во секое решение, различно подмножество од трите кружници е затворено во кружницата која е решение.

Аполониева заптивка

Слика 4. Симетрична Аполониева заптивка, наречена и Лајбницово пакување, по нејзиниот пронаоѓач Готфрид Лајбниц

Со повеќекратно решавање на проблемот на Аполониј за да се најде впишаниот круг, меѓусебните тангенцијални кружници може да се пополнат произволно ситно, формирајќи Аполониева заптивка, позната и како Лајбницово пакување или Аполониево пакување. Оваа заптивка е фрактал, кој е самосличен и има димензија $d$ која не е точно позната, но е приближно 1,3. Димензијата $d$ е повисока од онаа на правилна (или исправлива) крива,$d=1$, но e помалa од онaa на рамнината ($d=2$). Аполониевата заптивка првпат била опишана од Готфрид Лајбниц во XVII век и е закривен претходник на триаголникот на Сиерпински од XX век. Аполониевата заптивка, исто така, има длабоки врски со други области од математиката; на пример, тоа е граничното множество на Клајнови групи; види ја исто така теоремата за пакување на кругови.

Изодинамични точки на триаголник

Кружниците на Аполониј може да означуваат и три посебни кружници ${\mathcal {C}}_{1},{\mathcal {C}}_{2},{\mathcal {C}}_{3}$ дефинирани преку произволен триаголник $\mathrm {A_{1}A_{2}A_{3}}$. Кружницата ${\mathcal {C}}_{1}$ се дефинира како единствена кружница која минува низ темето $\mathrm {A_{1}}$ на триаголникот и за чии точки односот на растојанија до другите две темиња $\mathrm {A_{2}}$ и $\mathrm {A_{3}}$ е непроменлив (според дефиниција на Аполониј за кружница од погоре). Слично, кружницата ${\mathcal {C}}_{2}$ се дефинира како единствена кружница која минува низ темето на триаголникот $\mathrm {A_{2}}$ и која е ГМТ на точки за кои односот на растојанијата до другите две темиња $\mathrm {A_{1}}$ и $\mathrm {A_{3}}$ е константен; аналогно се дефинира и кружницата ${\mathcal {C}}_{3}$.

Сите три кружници ортогонално ја сечат опишаната кружница околу триаголникот. Сите три кружници минуваат низ две точки $S$ и $S^{\prime }$, кои се познати како изодинамични точки (изодинамични центри) на триаголникот. Правата која ги поврзува овие заеднички пресечни точки е радикалната оска за сите три кружници. Двете изодинамични точки се инверзни една на друга во однос на опишаната кружница на триаголникот.

Центрите на овие три кружници лежат на една права (правата на Lemoine). Оваа права е нормална на радикалната оска - правата одредена од изодинамичните точки.

Поврзано

• Аполониевка точка
• Елипса