Бернулиева распределба
Веројатносна функција
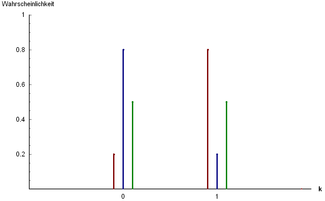
Три примери за Бернулиева распределба:
P
(
x
=
0
)
=
0
,
2
{\displaystyle P(x=0)=0{,}2}
и
P
(
x
=
1
)
=
0
,
8
{\displaystyle P(x=1)=0{,}8}
P
(
x
=
0
)
=
0
,
8
{\displaystyle P(x=0)=0{,}8}
и
P
(
x
=
1
)
=
0
,
2
{\displaystyle P(x=1)=0{,}2}
P
(
x
=
0
)
=
0
,
5
{\displaystyle P(x=0)=0{,}5}
и
P
(
x
=
1
)
=
0
,
5
{\displaystyle P(x=1)=0{,}5}
Параметри
0
≤
p
≤
1
{\displaystyle 0\leq p\leq 1}
q
=
1
−
p
{\displaystyle q=1-p}
Носител
k
∈
{
0
,
1
}
{\displaystyle k\in \{0,1\}}
ВФ
{
q
=
1
−
p
ако
k
=
0
p
ако
k
=
1
{\displaystyle {\begin{cases}q=1-p&{\text{ако }}k=0\\p&{\text{ако }}k=1\end{cases}}}
РФ
{
0
ако
k
<
0
1
−
p
ако
0
≤
k
<
1
1
ако
k
≥
1
{\displaystyle {\begin{cases}0&{\text{ако }}k<0\\1-p&{\text{ако }}0\leq k<1\\1&{\text{ако }}k\geq 1\end{cases}}}
Средина
p
{\displaystyle p}
Медијана
{
0
ако
p
<
1
/
2
[
0
,
1
]
ако
p
=
1
/
2
1
ако
p
>
1
/
2
{\displaystyle {\begin{cases}0&{\text{ако }}p<1/2\\\left[0,1\right]&{\text{ако }}p=1/2\\1&{\text{ако }}p>1/2\end{cases}}}
Модус
{
0
ако
p
<
1
/
2
0
,
1
ако
p
=
1
/
2
1
ако
p
>
1
/
2
{\displaystyle {\begin{cases}0&{\text{ако }}p<1/2\\0,1&{\text{ако }}p=1/2\\1&{\text{ако }}p>1/2\end{cases}}}
Варијанса
p
(
1
−
p
)
=
p
q
{\displaystyle p(1-p)=pq}
ПАО
1
2
{\displaystyle {\frac {1}{2}}}
Накосеност
q
−
p
p
q
{\displaystyle {\frac {q-p}{\sqrt {pq}}}}
Вишок зашиленост
1
−
6
p
q
p
q
{\displaystyle {\frac {1-6pq}{pq}}}
Ентропија
−
q
ln
q
−
p
ln
p
{\displaystyle -q\ln q-p\ln p}
МТФ
q
+
p
e
t
{\displaystyle q+pe^{t}}
КФ
q
+
p
e
i
t
{\displaystyle q+pe^{it}}
ВТФ
q
+
p
z
{\displaystyle q+pz}
Фишерова информација
1
p
q
{\displaystyle {\frac {1}{pq}}}
Бернулиева распределба во теоријата на веројатноста и статистиката — прекинатата веројатносна распределба на една случајна променлива која ја има вредноста 1 со веројатност
p
{\displaystyle p}
q
=
1
−
p
{\displaystyle q=1-p}
опит кој поставува прашање „да–не“. Ваквите прашања водат до исходи со една од две вредности: „успех“ (1) со веројатност p и „неуспех“ (0) со веројатност q . Со оваа распределба може да се претстави фрлање паричка каде 1 и 0 би биле „глава“ и „писмо“, а p би била веројатноста да се падне глава (или обратно, каде 1 е писмо, а p ќе биде веројатноста за писмо). Нечесните парички би имале
p
≠
1
/
2.
{\displaystyle p\neq 1/2.}
Наречена е по швајцараскиот математичар Јакоб Бернули [1] биномната распределба со еден спроведен опит (така што n би бил 1 за таква биномна распределба). Воедно таа претставува посебен случај на двоточкестата распределба , чии можни исходи не мора да бидат 0 и 1.
Ако
X
{\displaystyle X}
Pr
(
X
=
1
)
=
p
=
1
−
Pr
(
X
=
0
)
=
1
−
q
.
{\displaystyle \Pr(X=1)=p=1-\Pr(X=0)=1-q.}
Веројатносната фунција
f
{\displaystyle f}
k е
f
(
k
;
p
)
=
{
p
ако
k
=
1
,
q
=
1
−
p
ако
k
=
0.
{\displaystyle f(k;p)={\begin{cases}p&{\text{ако }}k=1,\\q=1-p&{\text{ако }}k=0.\end{cases}}}
[2] Ова може да се изрази и како
f
(
k
;
p
)
=
p
k
(
1
−
p
)
1
−
k
за
k
∈
{
0
,
1
}
{\displaystyle f(k;p)=p^{k}(1-p)^{1-k}\quad {\text{за }}k\in \{0,1\}}
или како
f
(
k
;
p
)
=
p
k
+
(
1
−
p
)
(
1
−
k
)
за
k
∈
{
0
,
1
}
.
{\displaystyle f(k;p)=pk+(1-p)(1-k)\quad {\text{за }}k\in \{0,1\}.}
Бернулиевата распределба е посебен случај на биномната распределба со
n
=
1.
{\displaystyle n=1.}
[3]
Зашиленоста оди до бесконечност за високи и ниски вредности на
p
,
{\displaystyle p,}
p
=
1
/
2
{\displaystyle p=1/2}
вишок зашиленост отколку било која друга веројатносна распределба, имено −2.
Бернулиевите распределби за
0
≤
p
≤
1
{\displaystyle 0\leq p\leq 1}
Процената на максимална веројатност на
p
{\displaystyle p}
Очекуваната вредност на една Бернулиева случајна променлива
X
{\displaystyle X}
E
[
X
]
=
p
{\displaystyle \operatorname {E} [X]=p}
Ова се должи на тоа што, за Бернулиево распределена случајна променлива
X
{\displaystyle X}
Pr
(
X
=
1
)
=
p
{\displaystyle \Pr(X=1)=p}
Pr
(
X
=
0
)
=
q
{\displaystyle \Pr(X=0)=q}
E
[
X
]
=
Pr
(
X
=
1
)
⋅
1
+
Pr
(
X
=
0
)
⋅
0
=
p
⋅
1
+
q
⋅
0
=
p
.
{\displaystyle \operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.}
[2] Варијансата на Бернулиево распределен
X
{\displaystyle X}
Var
[
X
]
=
p
q
=
p
(
1
−
p
)
{\displaystyle \operatorname {Var} [X]=pq=p(1-p)}
Прво имаме
E
[
X
2
]
=
Pr
(
X
=
1
)
⋅
1
2
+
Pr
(
X
=
0
)
⋅
0
2
=
p
⋅
1
2
+
q
⋅
0
2
=
p
=
E
[
X
]
{\displaystyle \operatorname {E} [X^{2}]=\Pr(X=1)\cdot 1^{2}+\Pr(X=0)\cdot 0^{2}=p\cdot 1^{2}+q\cdot 0^{2}=p=\operatorname {E} [X]}
Од ова следи
Var
[
X
]
=
E
[
X
2
]
−
E
[
X
]
2
=
E
[
X
]
−
E
[
X
]
2
=
p
−
p
2
=
p
(
1
−
p
)
=
p
q
{\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X]-\operatorname {E} [X]^{2}=p-p^{2}=p(1-p)=pq}
[2] Од овој резултат лесно е да се докаже дека, за секоја Бернулиева распределба, нејзината варијанса ќе има вредност во рамките на
[
0
,
1
/
4
]
{\displaystyle [0,1/4]}
Накосеноста (коефициентот на асиметрија) е
q
−
p
p
q
=
1
−
2
p
p
q
{\displaystyle {\frac {q-p}{\sqrt {pq}}}={\frac {1-2p}{\sqrt {pq}}}}
X
−
E
[
X
]
Var
[
X
]
{\displaystyle {\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}}
q
p
q
{\displaystyle {\frac {q}{\sqrt {pq}}}}
p
{\displaystyle p}
−
p
p
q
{\displaystyle -{\frac {p}{\sqrt {pq}}}}
q
{\displaystyle q}
γ
1
=
E
[
(
X
−
E
[
X
]
Var
[
X
]
)
3
]
=
p
⋅
(
q
p
q
)
3
+
q
⋅
(
−
p
p
q
)
3
=
1
p
q
3
(
p
q
3
−
q
p
3
)
=
p
q
p
q
3
(
q
−
p
)
=
q
−
p
p
q
.
{\displaystyle {\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}.\end{aligned}}}
Сите сирови моменти се еднакви поради тоа што
1
k
=
1
{\displaystyle 1^{k}=1}
0
k
=
0
{\displaystyle 0^{k}=0}
E
[
X
k
]
=
Pr
(
X
=
1
)
⋅
1
k
+
Pr
(
X
=
0
)
⋅
0
k
=
p
⋅
1
+
q
⋅
0
=
p
=
E
[
X
]
.
{\displaystyle \operatorname {E} [X^{k}]=\Pr(X=1)\cdot 1^{k}+\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=\operatorname {E} [X].}
k
{\displaystyle k}
μ
k
=
(
1
−
p
)
(
−
p
)
k
+
p
(
1
−
p
)
k
.
{\displaystyle \mu _{k}=(1-p)(-p)^{k}+p(1-p)^{k}.}
Првите шест централни моменти се
μ
1
=
0
,
μ
2
=
p
(
1
−
p
)
,
μ
3
=
p
(
1
−
p
)
(
1
−
2
p
)
,
μ
4
=
p
(
1
−
p
)
(
1
−
3
p
(
1
−
p
)
)
,
μ
5
=
p
(
1
−
p
)
(
1
−
2
p
)
(
1
−
2
p
(
1
−
p
)
)
,
μ
6
=
p
(
1
−
p
)
(
1
−
5
p
(
1
−
p
)
(
1
−
p
(
1
−
p
)
)
)
.
{\displaystyle {\begin{aligned}\mu _{1}&=0,\\\mu _{2}&=p(1-p),\\\mu _{3}&=p(1-p)(1-2p),\\\mu _{4}&=p(1-p)(1-3p(1-p)),\\\mu _{5}&=p(1-p)(1-2p)(1-2p(1-p)),\\\mu _{6}&=p(1-p)(1-5p(1-p)(1-p(1-p))).\end{aligned}}}
Вишите централни моменти може да се изразат покомпактно како
μ
2
{\displaystyle \mu _{2}}
μ
3
{\displaystyle \mu _{3}}
μ
4
=
μ
2
(
1
−
3
μ
2
)
,
μ
5
=
μ
3
(
1
−
2
μ
2
)
,
μ
6
=
μ
2
(
1
−
5
μ
2
(
1
−
μ
2
)
)
.
{\displaystyle {\begin{aligned}\mu _{4}&=\mu _{2}(1-3\mu _{2}),\\\mu _{5}&=\mu _{3}(1-2\mu _{2}),\\\mu _{6}&=\mu _{2}(1-5\mu _{2}(1-\mu _{2})).\end{aligned}}}
Првите шест кумуланти се
κ
1
=
p
,
κ
2
=
μ
2
,
κ
3
=
μ
3
,
κ
4
=
μ
2
(
1
−
6
μ
2
)
,
κ
5
=
μ
3
(
1
−
12
μ
2
)
,
κ
6
=
μ
2
(
1
−
30
μ
2
(
1
−
4
μ
2
)
)
.
{\displaystyle {\begin{aligned}\kappa _{1}&=p,\\\kappa _{2}&=\mu _{2},\\\kappa _{3}&=\mu _{3},\\\kappa _{4}&=\mu _{2}(1-6\mu _{2}),\\\kappa _{5}&=\mu _{3}(1-12\mu _{2}),\\\kappa _{6}&=\mu _{2}(1-30\mu _{2}(1-4\mu _{2})).\end{aligned}}}
Ако
X
1
,
…
,
X
n
{\displaystyle X_{1},\dots ,X_{n}}
Бернулиеви опити со веројатност за успех p , тогаш нивното множество е распределено според биномна распределба со параметри n и p :
∑
k
=
1
n
X
k
∼
B
(
n
,
p
)
{\displaystyle \sum _{k=1}^{n}X_{k}\sim \operatorname {B} (n,p)}
[2] Бернулиевата распределба едноставно е
B
(
1
,
p
)
{\displaystyle \operatorname {B} (1,p)}
B
e
r
n
o
u
l
l
i
(
p
)
.
{\textstyle \mathrm {Bernoulli} (p).}
Категоричната распределба е воопштувањето на Бернулиевата распределба за променливи со било кој постојан број на прекинати вредности.
Бета-распределбата е сврзувачкиот претходник of Бернулиевата распределба.Геометриската распределба го моделира бројот на независни и еднакви Бернулиеви опити потребни за да се добие еден успех.Ако
Y
∼
B
e
r
n
o
u
l
l
i
(
1
2
)
{\textstyle Y\sim \mathrm {Bernoulli} \left({\frac {1}{2}}\right)}
2
Y
−
1
{\textstyle 2Y-1}
↑ James Victor Uspensky: Introduction to Mathematical Probability , McGraw-Hill, New York 1937, стр. 45
↑ 2,0 2,1 2,2 2,3 Bertsekas, Dimitri P. (2002). Introduction to Probability . Tsitsiklis, John N., Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific. ISBN 188652940X OCLC 51441829 . ↑ McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition . Boca Raton: Chapman and Hall/CRC. Section 4.2.2. ISBN 0-412-31760-5













![{\displaystyle {\begin{cases}0&{\text{ако }}p<1/2\\\left[0,1\right]&{\text{ако }}p=1/2\\1&{\text{ако }}p>1/2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2653cf6608e09c52e4f9c5aeef62bcf0eef39fde)




















![{\displaystyle \operatorname {E} [X]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb41a45634ab84b13b83cb1488b626aa2129285)


![{\displaystyle \operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5011326253761bfe33bc3d51773a83268b8a56b7)
![{\displaystyle \operatorname {Var} [X]=pq=p(1-p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d4e26d8a1fdfb90e91a2fafd5fb3841de88f1fb)
![{\displaystyle \operatorname {E} [X^{2}]=\Pr(X=1)\cdot 1^{2}+\Pr(X=0)\cdot 0^{2}=p\cdot 1^{2}+q\cdot 0^{2}=p=\operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bf32718a7a52087297a46d9ebc177ee0c80df07)
![{\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X]-\operatorname {E} [X]^{2}=p-p^{2}=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41972e4aade1430eb47d46a91051f00a583e0c45)
![{\displaystyle [0,1/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604604d2122dc1c25141a841483b889d6832f261)

![{\displaystyle {\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bdd3a134128b0517590174937df60485f0828d0)



![{\displaystyle {\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5c4b867e768adc821f038408b00a6c8bdce2e4)


![{\displaystyle \operatorname {E} [X^{k}]=\Pr(X=1)\cdot 1^{k}+\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=\operatorname {E} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cbafd464e73d482dc6c32d1c4f3eaedd5539952)












