Шестаголник
| Правилен шестаголник | |
|---|---|
 Правилен шестаголник | |
| Вид | правилен многуаголник |
| Рабови и темиња | 6 |
| Шлефлиев симбол | {6}, t{3} |
| Коксетер–Динкинови дијаграми | |
| Група на симетрија | диедарска (D6), ред 2×6 |
| Внатрешен агол | 120° |
| Својства | испакнат, впишан, рамностран, изогонален, изотоксален |
Шестаголник — многуаголник со шест темиња и шест страни.
Правилен шестаголник
[уреди | уреди извор]Правилниот шестаголник е шестаголник кај кого сите страни се со еднакви должини и сите внатрешни агли се еднакви.
Внатрешните агли на правилен шестаголник имаат по 120° (степени), а збирот на сите внатрешни агли на кој било шестаголник изнесува 720°. Како што е можно да се покрие рамнина со рамнострани триаголници или квадрати, и правилниот шестаголник ја има таа особина.
Пчелното саќе има основни елементи во облик на шестаголник токму затоа што таквата форма овозможува ефикасна и економична употреба на просторот и материјалот од кого е изградено.
Ако забележиме дека правилниот шестаголник е составен од 6 рамнострани триаголници, неговата површина ќе биде шест пати поголема од површината на рамностран триаголник и ако неговата страна е со должина , ќе биде дадена со формулата:[1]
Периметарот на шестаголник чија страна е со должина е еднаков на , должината на дијагоналата е .
Конструкција
[уреди | уреди извор]Правилен шестаголник може да се конструира со помош на линијар и шестар. Следнава анимација ја илустрира чекор по чекор конструкцијата на правилен шестаголник која ја дал Евклид во своите „Елементи“.

Неправилни шестаголници
[уреди | уреди извор]Секој шестаголник кој не е правилен се нарекува неправилен. Овој вид може да ги има следниве облици:
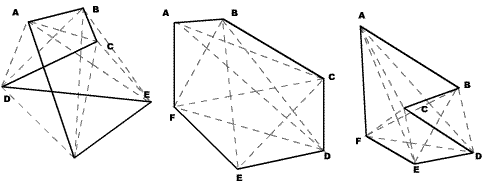 | ||
| Вкрстен шестаголник | Испакнат шестаголник | Вдлабнат шестаголник |
| Темиња | Страни | Дијагонали |
| 6 | 6 | 9 |
Каде може да се види шестаголник
[уреди | уреди извор]-
Поглед од воздух на Форт Џеферсон во националнион парк Драј Тортугас
-
Пчелно саќе
-
Микрофотографија на снегулка
Поврзано
[уреди | уреди извор]- Многуаголник
- Правилен многуаголник
- Четириаголник
- Петаголник
- Седумаголник
- Осумаголник
- Деветаголник
- Десетаголник
Надворешни врски
[уреди | уреди извор]| „Шестаголник“ на Ризницата ? |
- Шестаголник на Mathworld
- Дефиниција и особини на шестаголник со интерактивна анимација
| ||||||||||||||||||||||
- ↑ Боривоје Миладиновиќ, Трајче Ѓорѓијевски и Никола Петрески, Математика за II година гимназиско образование. Скопје: Алби, 2009, стр. 135.







