Троутон-Ноблов опит

Кружен кондензатор B, со пречник од 7,7 cm, изграден од повеќе слоеви на микашист и станиол, сместен во мазен сферичен целулозна топка D која е препокриена со проводна боја, и била затегната со фина фосфоро-бронзена жица долга 37 см во заземјена цевка. Жицата била поврзана со една електрода на Вимхурстовата машина која ги одржувала плочите на кондензаторот под напон од 3000 волти. Спротивните плочи на кондензаторот како и самата целулозна топка биле заземјени со жица од платина потопена во сулфурна киселина која не служела само како спроводна електрода , туку и ги придушувала осцилациите и дејствувала како исушувач. Огледало прикачено на кондензаторот било набљудувано преку телескоп и дозволувало да се направат мали измени во просторната насоченост за набљудување.

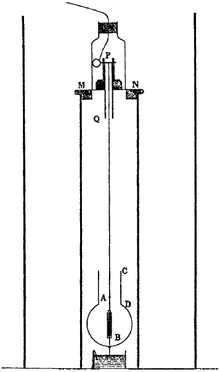
Троутон-Ноблов опит — опит да се открие движењето на Земјата низ етерот. Овој опит бил спроведен од 1901-1903 од страна на Фредерик Томас Троутон и Х.Р.Нобл. Тој бил заснован на предлогот од Џорџ Фицџералд според кој наелектризиран кондензатор со паралелна плоча, кој се движи низ етер треба самиот да се ориентира нормално во однос на движењето. Како и при Мајкелсон-Морлиевиот обид, Трутон и Нобл добиле нулта резултат: не можело да се забележи ниту едно движење релативно кон етерот. Нулта резултатот бил репродуциран со зголемена чувствителност од страна на Рудолф Томачек, Чејс и Хајден.

Такви експериментални резултати сега можат да се видат со специјална релативност за да ја рефлектираат валидноста на принципот на релативност и отсуството на апсолутна рамка за одмор (или етер). Трутон-Нобелиовиот експеримент е исто така поврзан со експриментот на мислата како на пример Трутон-Нобеловиот парадокс или парадоксот Луис-Толман. Неколку можни решенија беа предложени за да се реши овој тип на парадокси, во согласност со специајалната релативност.

Трутон-Ноблов опит

Во експериментот, суспендираниот кондензатор со паралелна плоча се држи на фино извртен конец и се полни. Ако теоријата за етерот беше точна, промената во Максвеловата равенка поради движењето на Земјата низ етерот би довела до вртежен момент, што би ги довела плочките да се израмнат/усогласат нормално со движењето. Ова е дадено во равенката:

$\tau =-E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '$

Каде $\tau$ е вртежниот момент,$E$ е енергијата на кондензаторот, $\alpha$ е аголот помеѓу нормалата на плочката и брзината. Од друга страна, тврдењето на специјланата релативност дека Максвеловите равенки се непроменливи за сите рамки на рефернца кои се движат со константна брзина би предвидиле нулта резултат односно не би имало вртежен момент. Така, освен ако етерот е фиксиран во однос на Земјата, експериментот е тест за онаа теорија која е поточна. Нулта резултат, пак, ја потврдува Лоренцовата непроменлива за специјалната релативност.

Меѓутоа, додека негативниот исход лесно може да се објасни за рамката на мирување на уредот, објаснувањето од гледна точка на неподвижната рамка е многу потешко и се нарекува Трутон-Нобелов парадокс, кој може да се реши на повеќе начини.

Парадоксот на лостот под прав агол

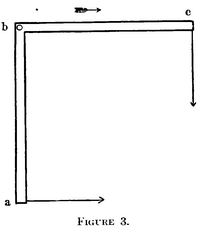
Трутон-Нобеловиот парадокс е суштински еднаков на мисловниот експеримент наречен парадоксто на лостот под прав агол, кој за првпат бил претставен од Гилберт Њутон Луис и Ричард Чејс Толман во 1909 година. Претставете си лост под прав агол со крајни точки abc. Во неговата рамка на мирување, силите $f_{y}$ кон ba и на $f_{x}$ кон bc мора да бидат еднакви за да постигнат еквилибриум, така што нема да се постигне вртежен момент по законот на лостот:

$\tau '=L_{0}\left(f'_{x}-f'_{y}\right)=0$

Каде $\tau$ е вртежниот момент и $L_{0}$ е останатата должина од едно-лостовата рака. Сепак, благодарение на контракцијата на должината,ba е подолго од bc во еден неподвижен систем и затоа законот на лостот дава:

$\tau =f_{x}\cdot L_{0}-f_{y}\cdot L_{0}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}=L_{0}\left(f_{x}-f_{y}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)$

Може да се види дека вртежниот момент не е нула, што најверојатно би довело до тоа лостот да се ротира во една неподвижна рамка. Бидејќи нема видлива ротација, Луис и Толман заклучиле дека не постои ни вртежен момент и затоа:

${\frac {f_{x}}{f_{y}}}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

Но, како што било покажан од Макс фон Лу во 1911 г., ова е контрадикторно на релативистичката експресија на силата,

$f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

што дава,

${\frac {f_{x}}{f_{y}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

Кога ова ќе се примени на законот на лотосот, се добива следниов вртеж:

$\tau =-L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}}$

кој во суштина е истиот проблем како и при Трутон-Нобеловиот парадокс.

Решенија

Деталната релативистичка анализа на Трутон-Нобеловиот парадокс и парадоксот на лостот под прав агол треба да се разгледуваат внимателно, како на пример, ефектите видени од набљудувачите во различни референти рамки- но на крајот на краиштата сите теортски описи го даваат истиот резултат. И во двата случаи еден очигледен вртеж на обојет (кога се набљудува од одредена референта рамка), не резултира со ротација на објектот и и во двата случаи ова се објаснува преку точното пресметување на релативен начин на трансформацијата на релевантните сили, моментумот и забрзувањата предизвикани од нив. Раната историја на описи на овој експеримент била разгледана од Јансен во 1995 година.

Луовиот проток

Првото решение на Трутон-Нобеловиот парадокс било дадено од Хендрик Лоренц во 1904 година. Неговиот резултат се заснова на претпоставката дека вртежот и моментумот предизвикани од електростатичките сили се компензира од вретжот и моментумот предизвикани од молекуларните сили. Ова подоцна било елаборирано од Макс фон Лу во 1911 г., кој го дал стандардното решение за овој тип на парадокси. Решението било засновано на таканаречената „инерција на енергијата“ како што е дефинирана од Макс Планк. Според Лу, енергијата која е момнтално поврзана за одреден моментум ( Луовиот проток) е произведена од телата кои се движат по еластичен напреѓања. Тоа резултира во механички вртеж, кој во Трутон-Нобеловиот експеримент е еднаков на:

$\tau =E'{\frac {v^{2}}{c^{2}}}\sin 2\alpha '$

И во лостот под прав агол:

$\tau =L_{0}\cdot f'_{x}\cdot {\frac {v^{2}}{c^{2}}}$

Што точно го компензира електромагнетното вртење спомнато погоре, и на овој начин и во двата случи нема ротација.Со други зборови: Електромагнетниот вртеж е всушност потребен за униформираното движење на телото т.е. да го спречи телото да ротира поради механичкиот вртеж предизвикан од еластичното напреѓање. Оттогаш има многу издадени трудови кои елаборираат за Луровиот проток и нудат неколку измени или реинтерпретации, кои вклучуваат различни варијанти на „скриен“ моментум.

Преформулации на силата и моментумот

Група на автори биле незадоволни со идејата дека вртежот и против-вртежот се случуваат само затоа што се избрани различни инертни рамки. Нивна цел била да ги заменат стандардните искажувања за моментумот и силата и еквилибриумот. Така што кога нема вртеж во рамката на мирување на објектот во прашање, нема да има вртежи ни во другите рамки.. Оваа теорија е направена како аналогија на 4/3 проблемот на електромагнетната маса на електрони, каде што слични методи биле спроведени од Енрико Ферми во 1921 г. и Фриц Рорлих во 1960 г.: Во стандардната формулација за релативната динамика, секој набљудувач може да ја користи хипер-површината на симултаноста, додека во дефиницијата од Феми/Рорлих се користи хипер-површината на симултаноста од рамката на мирување на објектот. Според Јансен, дали би се одлучиле за Луовиот стандарден модел или за некоја од алтернативите е прашање на лично убедување. r reading</ref> Следејќи го овој модел на размислување, Рорлих ја направил разликата помеѓу „очигледни“ и „вистинити“ Лоренцови трансформации. На примепм, „вистинска“ трансформација на должинат би била резултатот на директната апликација на Лоренцовата трансформација, која ги дава несимултаните позиции на крајните точки од друга рамка. Од друга страна, контракцијата на должината би била пример за очигледна трансформија, бидејќи симултаните позиции на крајните точки од рамката на движење мора да бидат искалкулирани дополнително во првоначалната Лоренцова трансформација. Кавалери и Салгарели (1969г.) ја прават разликата помеѓу „синхрони“ и „асинхрони“ услови на еквилибриум. Според нивното мислење, синхрони сили треба да се користат само за рамката на мирување на објектот, додека за рамката на движење истити сили треба да бидат искористени асинхроно.

Сила и забрзување

Ричард Ц.Толман и Пол Софус Епстин објавиле решение во 1911 г. Кое не вклучувало компензирачки сили или редефиниции на силата и еквилибриумот. Слично решение било откриено од страна на Франклин во 2006 г. Тие алудирале на фактот дека силата и забрзувањето не секогаш ја имаат истата насока, т.е. релацијата на масата, силата и забрзувањето има тензорен карактер во релативноста. Тоа значи дека улогата на концептот за силата во релативноста е многу поразлична од онаа во Њутоновата механика. Епстин замислил прачка без маса со крајни точки ОМ, која е монтирана на точката О, и една честичка со маса на мирување m е монтирана во точката М. Прачката го опфаќа аголот со О. Применувјќи сила кон ОМ во точката М, се постигнува еквилибриум во рамката на мирување кога.Како што беше покажано погоре, овие сили ја имаат формата во неподвижна рамка:

$f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}},\ \tan \alpha =\tan \alpha '{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

И оттаму: ${\frac {f_{x}}{f_{y}}}={\frac {\tan \alpha }{1-{\frac {v^{2}}{c^{2}}}}}$. Резултантната сила не тргнува директно од О кон М. Но дали ова води до ротација на прачката? Не, бидејќи Епстин сега го зема предвид забрзувањето предизвикано од двете сили. Релативната експресија во случајот кога масата mсе забрзува од две сили во надолжна и попречна насока е еднаква на:

$a_{x}={\frac {f_{x}}{m\gamma ^{3}}},\ a_{y}={\frac {f_{y}}{m\gamma }}$, where $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$.

И оттаму: ${\frac {a_{x}}{a_{y}}}=\tan \alpha$. На овој начин немаме никава ротација во системот. Слични размислувања се применуваат и на лостот под прав агол и на Трутон-Нобеловиот експеримент. На овој начин се решаваат парадоксите, бидејќи двете забрзувања (како вектори) се насочени кон центарот на гравитација на системот, иако двете сили не го прават. Епстин додал дека ако на некој му причинува поголемо задаволство да повторно да ја воспостави паралелата помеѓу силата и забрзувањето на кои сме навикнати во Њутоновата механика, тогаш тој треба да ја вклучи и компензираната сила, која формално кореспондира на Луровиот проток. Епстин развил таков формализам во додадените параграфи во неговиот труд од 1911 година.

Поврзано

• Историја на специјалната релативност

Дополнителна литература

Историја

• Michel Janssen, "A comparison between Lorentz's ether theory and special relativity in the light of the experiments of Trouton and Noble, Ph.D. thesis (1995). Online: TOC, 1, 2, 3, 4, refs.
• Janssen, Michel H. P. (2008), „Drawing the line between kinematics and dynamics in special relativity“, Symposium on Time and Relativity: 1–76

Учебници

• Tolman, R.C. (1917), „The Right-Angled Lever“, The theory of relativity of motion, Berkeley: University of California press, стр. 539–776, 152–153
• Pauli, Wolfgang (1981) [1921]. „Applications to special cases. Trouton's and Noble's experiment“. Theory of Relativity. New York: Dover. стр. 127–130. ISBN 0-486-64152-X.
• Panofsky, Wolfgang; Phillips, Melba (2005) [1962]. Classical electricity and magnetism. Dover. стр. 274, 349. ISBN 0-486-43924-0.CS1-одржување: повеќе имиња: список на автори (link)
• Jackson, John D. (1998). Classical Electrodynamics (3. изд.). Wiley. ISBN 0-471-30932-X.

Американско списание за физиката

• Gamba, A. (1967). „Physical Quantities in Different Reference Systems According to Relativity“. American Journal of Physics. 35 (2): 83–89. Bibcode:1967AmJPh..35...83G. doi:10.1119/1.1973974.
• Butler, J. W. (1968). „On the Trouton-Noble Experiment“. American Journal of Physics. 36 (11): 936–941. Bibcode:1968AmJPh..36..936B. doi:10.1119/1.1974358.
• Aranoff, S. (1969). „Torques and Angular Momentum on a System at Equilibrium in Special Relativity“. American Journal of Physics. 37 (4): 453–454. Bibcode:1969AmJPh..37..453A. doi:10.1119/1.1975612.
• Furry, W. H. (1969). „Examples of Momentum Distributions in the Electromagnetic Field and in Matter“. American Journal of Physics. 37 (6): 621–636. Bibcode:1969AmJPh..37..621F. doi:10.1119/1.1975729.
• Butler, J. W. (1969). „A Proposed Electromagnetic Momentum-Energy 4-Vector for Charged Bodies“. American Journal of Physics. 37 (12): 1258–1272. Bibcode:1969AmJPh..37.1258B. doi:10.1119/1.1975297.
• Butler, J. W. (1970). „The Lewis-Tolman Lever Paradox“. American Journal of Physics. 38 (3): 360–368. Bibcode:1970AmJPh..38..360B. doi:10.1119/1.1976326.
• Rohrlich, F. (1970). „Electromagnetic Momentum, Energy, and Mass“. American Journal of Physics. 38 (11): 1310–1316. Bibcode:1970AmJPh..38.1310R. doi:10.1119/1.1976082.
• Sears, Francis W. (1972). „Another Relativistic Paradox“. American Journal of Physics. 40 (5): 771–773. Bibcode:1972AmJPh..40..771S. doi:10.1119/1.1986643.
• Aranoff, S. (1973). „More on the Right-Angled Lever at Equilibrium in Special Relativity“. American Journal of Physics. 41 (9): 1108–1109. Bibcode:1973AmJPh..41.1108A. doi:10.1119/1.1987485.
• Nickerson, J. Charles; McAdory, Robert T. (1975). „The Trouton-Noble paradox“. American Journal of Physics. 43 (7): 615–621. Bibcode:1975AmJPh..43..615N. doi:10.1119/1.9761.CS1-одржување: повеќе имиња: список на автори (link)
• Cavalleri, G.; Grøn, Ø.; Spavieri, G.; Spinelli, G. (1978). „Comment on the article "Right-angle lever paradox" by J. C. Nickerson and R. T. McAdory“. American Journal of Physics. 46 (1): 108–109. Bibcode:1978AmJPh..46..108C. doi:10.1119/1.11106.CS1-одржување: повеќе имиња: список на автори (link)
• Grøn, Ø. (1978). „Relativistics statics and F. W. Sears“. American Journal of Physics. 46 (3): 249–250. Bibcode:1978AmJPh..46..249G. doi:10.1119/1.11164.
• Holstein, Barry R.; Swift, Arthur R. (1982). „Flexible string in special relativity“. American Journal of Physics. 50 (10): 887–889. Bibcode:1982AmJPh..50..887H. doi:10.1119/1.13002.CS1-одржување: повеќе имиња: список на автори (link)
• Singal, Ashok K. (1993). „On the "explanation" of the null results of Trouton-Noble experiment“. American Journal of Physics. 61 (5): 428–433. Bibcode:1993AmJPh..61..428S. doi:10.1119/1.17236.
• Teukolsky, Saul A. (1996). „The explanation of the Trouton-Noble experiment revisited“. American Journal of Physics. 64 (9): 1104–1109. Bibcode:1996AmJPh..64.1104T. doi:10.1119/1.18329.
• Jackson, J. D. (2004). „Torque or no torque? Simple charged particle motion observed in different inertial frames“. American Journal of Physics. 72 (12): 1484–1487. Bibcode:2004AmJPh..72.1484J. doi:10.1119/1.1783902.

Европско списание за физиката

• Aguirregabiria, J. M.; Hernandez, A.; Rivas, M. (1982). „A Lewis-Tolman-like paradox“. European Journal of Physics. 3 (1): 30–33. Bibcode:1982EJPh....3...30A. doi:10.1088/0143-0807/3/1/008.CS1-одржување: повеќе имиња: список на автори (link)
• Franklin, Jerrold (2006). „The lack of rotation in the Trouton Noble experiment“. European Journal of Physics. 27 (5): 1251–1256. arXiv:physics/0603110. Bibcode:2006EJPh...27.1251F. doi:10.1088/0143-0807/27/5/024.
• Franklin, Jerrold (2008). „The lack of rotation in a moving right angle lever“. European Journal of Physics. 29 (6): N55–N58. arXiv:0805.1196. Bibcode:2008EJPh...29...55F. doi:10.1088/0143-0807/29/6/N01.

Списание за физика А

• Jefimenko, Oleg D. (1999). „The Trouton-Noble paradox“. Journal of Physics A. 32 (20): 3755–3762. Bibcode:1999JPhA...32.3755J. doi:10.1088/0305-4470/32/20/308.

Нуово Кименто

• Arzeliès, H. (1965). „Sur le problème relativiste du levier coudé“. Il Nuovo Cimento. 35 (3): 783–791. doi:10.1007/BF02739341.
• Rohrlich, F. (1966). „True and apparent transformations, classical electrons, and relativistic thermodynamics“. Il Nuovo Cimento B. 45 (1): 76–83. Bibcode:1966NCimB..45...76R. doi:10.1007/BF02710587.
• Newburgh, R. G. (1969). „The relativistic problem of the right-angled lever: The correctness of the Laue solution“. Il Nuovo Cimento B. 61 (2): 201–209. Bibcode:1969NCimB..61..201N. doi:10.1007/BF02710928.
• Cavalleri, G.; Salgarelli, G. (1969). „Revision of the relativistic dynamics with variable rest mass and application to relativistic thermodynamics“. Il Nuovo Cimento A. 62 (3): 722–754. Bibcode:1969NCimA..62..722C. doi:10.1007/BF02819595.CS1-одржување: повеќе имиња: список на автори (link)
• Aranoff, S. (1972). „Equilibrium in special relativity“ (PDF). Il Nuovo Cimento B. 10 (1): 155–171. Bibcode:1972NCimB..10..155A. doi:10.1007/BF02911417. Архивирано од изворникот (PDF) на 2012-03-28. Посетено на 2015-11-01.
• Grøn, Ø. (1973). „The asynchronous formulation of relativistic statics and thermodynamics“. Il Nuovo Cimento B. 17 (1): 141–165. Bibcode:1973NCimB..17..141G. doi:10.1007/BF02906436.
• Pahor, S.; Strnad, J. (1974). „Statics in special relativity“. Il Nuovo Cimento B. 20 (1): 105–112. Bibcode:1974NCimB..20..105P. doi:10.1007/BF02721111.CS1-одржување: повеќе имиња: список на автори (link)
• Cavalleri, G.; Spavieri, G.; Spinelli, G. (1975). „Ropes and pulleys in special relativity (relativistic statics of threads)“. Il Nuovo Cimento B. 25 (1): 348–356. Bibcode:1975NCimB..25..348C. doi:10.1007/BF02737685.CS1-одржување: повеќе имиња: список на автори (link)
• Chamorro, A.; Hernández, A. (1978). „A synchronous formulation of relativistic statics“. Il Nuovo Cimento B. 41 (1): 236–244. Bibcode:1977NCimB..41..236C. doi:10.1007/BF02726555.CS1-одржување: повеќе имиња: список на автори (link)
• Hernández, A.; Rivas, M.; Aguirregabiria, J. M. (1982). „A quantitative analysis of the trouton-noble experiment“. Il Nuovo Cimento B. 72 (1): 1–12. Bibcode:1982NCimB..72....1H. doi:10.1007/BF02894929.CS1-одржување: повеќе имиња: список на автори (link)
• Ai, Hsiao-Bai (1993). „The historical misconception in relativistic statics“. Il Nuovo Cimento B. 108 (1): 7–15. Bibcode:1993NCimB.108....7A. doi:10.1007/BF02874335.
• Nieves, L.; Rodriguez, M.; Spavieri, G.; Tonni, E. (2001). „An experiment of the Trouton-Noble type as a test of the differential form of Faraday's law“. Il Nuovo Cimento B. 116 (5): 585. Bibcode:2001NCimB.116..585N.CS1-одржување: повеќе имиња: список на автори (link)
• Spavieri, G.; Gillies, G. T. (2003). „Fundamental tests of electrodynamic theories: Conceptual investigations of the Trouton-Noble and hidden momentum effects“. Il Nuovo Cimento B. 118 (3): 205. Bibcode:2003NCimB.118..205S.CS1-одржување: повеќе имиња: список на автори (link)

Основите на физиката

• Prokhovnik, S. J.; Kovács, K. P. (1985). „The application of special relativity to the right-angled lever“. Foundations of Physics. 15 (2): 167–173. Bibcode:1985FoPh...15..167P. doi:10.1007/BF00735288.CS1-одржување: повеќе имиња: список на автори (link)
• Spavieri, Gianfranco (1990). „Proposal for experiments to detect the missing torque in special relativity“. Foundations of Physics Letters. 3 (3): 291–302. Bibcode:1990FoPhL...3..291S. doi:10.1007/BF00666019.
• Ivezić, Tomislav (2005). „Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment“. Foundations of Physics Letters. 18 (5): 401–429. arXiv:physics/0412167. Bibcode:2005FoPhL..18..401I. doi:10.1007/s10702-005-7533-7.
• Ivezić, Tomislav (2006). „Four-Dimensional Geometric Quantities versus the Usual Three-Dimensional Quantities: The Resolution of Jackson's Paradox“. Foundations of Physics. 36 (10): 1511–1534. arXiv:physics/0602105. Bibcode:2006FoPh...36.1511I. doi:10.1007/s10701-006-9071-y.
• Ivezić, Tomislav (2006). „Trouton Noble Paradox Revisited“. Foundations of Physics. 37 (4–5): 747–760. arXiv:physics/0606176. Bibcode:2007FoPh...37..747I. doi:10.1007/s10701-007-9116-x.

Надворешни врски

• Kevin Brown, "Trouton-Noble and The Right-Angle Lever at MathPages.
• Michel Janssen, "The Trouton Experiment and E = mc² Архивирано на 17 октомври 2015 г.," Einstein for Everyone course at UMN (2002).