Лак (геометрија)
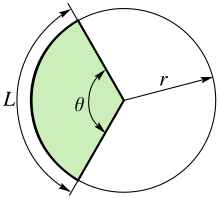
Лак[1][2] — дел од крива во геометријата ограничен со две точки на таа крива[3]. На пример, лак на круг е дел од обемот на кружницата, но исто толку можеме да зборуваме за лак на парабола или на елипса.
Тетива е отсечка што ги спојува краевите на лакот[3].
Стрелката е права нормална на тетивата и минува низ точката на лакот најоддалечена од тетивата[3] .
Се вели дека лакот е конвексен ако секоја права линија не може да го пресече на повеќе од две точки. Кривина (глобална) на конвексен лак е аголот формиран од тангентите на двата краја на лакот[3].
- За аналитичко проучување на лаковите, во рамнина и во n-димензионални векторски простори, видете Параметарски лак;
- За целиот вокабулар поврзан со параметарски лакови, видете Лексикон на параметарски лакови.
Наводи
[уреди | уреди извор]- ↑ „лак“ — Дигитален речник на македонскиот јазик
- ↑ „лак“ — Официјален дигитален речник на македонскиот јазик
- 1 2 3 4 Augustin Privat-Deschanel; Adolphe Jean Focillon (1864). Dictionnaire général des sciences. 1. Tandou, Victor Masson et Garnier Frères. стр. 149 Arc (géométrie).
