Квадар
| Квадар | |
|---|---|
| |
| Вид | Призма |
| Страни | 6 правоаголници |
| Рабови | 12 |
| Темиња | 8 |
| Група на симетрија | D2h (*222) |
| Својства | испакнатост, зоноедар, изогоналност |
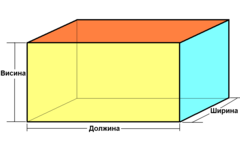
Во геометријата, квадар (наречен и квадратна призма) е геометриско тело со шест правоаголни страни, т.е. личи на правоаголна кутија. Сите агли се прави, а спротивните страни на квадарот се еднакви. Ова е исто правоаголна призма.
Квадратниот квадар (наречен и квадратна призма) е посебен вид на квадар кај кој најмалку две страни се квадрати. коцката е посебен случај на квадратна призма, каде сите шест страни се квадрати.
Ако димензиите на квадарот се a, b и c, тогаш неговиот волумен ќе биде abc, а неговата плоштина ќе биде 2ab + 2bc + 2ac.
Должината на просторна дијагонала е
Квадарот е испакнат полиедар. Неговите страни заградуваат еден единствен простор. Тој има 6 страни, 8 темиња и 12 рабови.
Ојлеровата формула вели дека бројот на страни (С), темиња (Т), и рабови (Р) на еден полиедар се во сооднос по формулата С + Т = Р + 2, што во овој случај е 6 + 8 = 12 + 2.
Квадарните облици често се користат за кутии, креденци, соби, згради итн. Квадарот им припаѓа на телата кои можат да поплочат 3-димензионален простор. Обликот му е прилично сестран, во можност самиот да содржи повеќе помали квадари, на пр. шеќерните коцки во кутија, помали кутии во поголема, креденец во соба, како и собите во куќата.
Квадар чиишто должини на рабовите и дијагоналите изнесуваат цели броеви (недецимални) се нарекува Ојлерова цигла, како на пример со страни од 44, 117 страни од 240. Совршен квадар е Ојлерова цигла чија просторна дијагонала е со должина од исто така цел број. Моментално е непознато дали совршен квадар навистина постои.
Формули[уреди | уреди извор]

Во табелата се дадени почесто користените формули за квадар:
| Површина | |
| Зафатнина | |
| Мали дијагонали | |
| Голема дијагонала | |
| Полупречник на опишана сфера | |
| Аголот меѓу големата дијагонала и основата |
Поврзано[уреди | уреди извор]
Надворешни врски[уреди | уреди извор]
|









