Унија (теорија на множества)

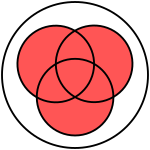
Унија (со ознака ∪) на одредена група множества – множество од сите елементи во групата.[1] Таа е една од фундаменталните операции со која множествата можат да се комбинираат и меѓусебно поврзуваат.
Унија на две множества[уреди | уреди извор]
Унија на две множества А и В е множеството елементи кои се елементи на множествата А, В или во А и В “. Изразено со симболи,
- .[2]
На пример, ако А = {1, 3, 5, 7} и B = {1, 2, 4, 6} тогаш A ∪ B = {1, 2, 3, 4, 5, 6, 7}. Посложен пример (кој вклучува две бесконечни множества) е:
- A = {x е непарен цел број поголем од 1}
- B = {x е парен цел број поголем од 1}
Множествата не можат да имаат дупли елементи,[2][3] следствено унијата на множествата {1, 2, 3} и {2, 3, 4} е {1, 2, 3, 4}. Повеќекратното присуство на идентични елементи нема ефект на кардиналноста на множеството или неговата содржина.
Алгебарски својства[уреди | уреди извор]
Бинарната унија е асоцијативна операција; така,
Операциите може да се извршуваат по кој било редослед и заградите може да се испуштат без промени на резултатот (горниот израз еквивалентно може да се изрази како A ∪ B ∪ C).
Слично, унијата е комутативна, па множествата може да бидат напишани по кој било редослед.[4]
Празното множество е неутрален елемент за операцијата унија. Така, A ∪ ∅ = A, за кое било множество A. Ова следи од аналогните факти за логичката дисјункција.
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ Weisstein, Eric W. „Union“. Wolfram's Mathworld.
- ↑ 2,0 2,1 Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (2002-01-01). Basic Set Theory (англиски). American Mathematical Soc. ISBN 9780821827314.
- ↑ deHaan, Lex; Koppelaars, Toon (2007-10-25). Applied Mathematics for Database Professionals (англиски). Apress. ISBN 9781430203483.
- ↑ Halmos, P. R. (2013-11-27). Naive Set Theory (англиски). Springer Science & Business Media. ISBN 9781475716450.
Надворешни врски[уреди | уреди извор]
 Унија (теорија на множества) на Ризницата
Унија (теорија на множества) на Ризницата- „Union“ од Ерик В. Вајсштајн — MathWorld (англиски)
- Хацевинкел, Михил, уред. (2001), „Union of sets“, Математичка енциклопедија, Шпрингер, ISBN 978-1556080104
- Infinite Union and Intersection at ProvenMath De Morgan's laws formally proven from the axioms of set theory.





