Логички двоуслов
Логички двоуслов (наречен и материјален двоуслов или бикондиционал) — логички опратор кој поврзува два исказа „p ако и само ако q“, каде p е хипотеза (или претходник), а q е заклучок (или следственик).[1] Овој оператор се означува со двострана стрелка (↔), знак за еднаквост (=), знак за еквиваленција (≡), или пак EQV. Ова е логички еквивалентно на (p → q) ∧ (q → p), или Буловиот оператор ЕКСНИЛИ (исклучително НИЛИ) . Ова е еквивалентно на „(не p или q) и (не q или p)“. Логички е еквивалентно и на „(не p и не q) или (p и q)“.
Хипотезата понекаде се нарекува и „доволен услов“ додека пак заклучокот може да се нарече „неопходен услов“.
Единствената разлика од материјалниот услов е случајот каде што хипотезата е невистинита, но заклучокот е вистинит. Во тој случај резултатот е вистинит, но сепак во двоусловот резултатот е невистинит.
По концептуално (идејно) толкување, a = b значи „Сите a се b и сите b се a“; со други зборови, множествата a и b се совпаѓаат: идентични се. Ова не значи дека концептите имаат исто значење. На пример: „триаголник“ и „тристран“, „рамноаголен триаголник“ и „рамностран триаголник“. Претходникот е подмет, а следственикот е прирок на еден универзален потврден исказ.
По исказно толкување, a ⇔ b значи дека a имплицира b и b имплицира a; со други зборови, дека исказите се еквивалентни, т.е. едновремено или вистинити или невистинити. Ова не значи дека тие се со исто значење. На пример: „Триаголникот ABC има две еднакви страни“, и „Триаголникот ABC има два еднакви агли“. Претходникот е премисата или причинителот, а следственикот е последицата. Кога една импликација ќе се преведе во хипотетичко (или условно) расудување, претходникот се нарекува хипотеза (или услов), а следственикот се нарекува теза.
Често двоусловот се илустрира со употреба на еквиваленција на конјункцијата на два обратни услови, покажувајќи ги посебно.
Кога двата елемента на двоусловот се искази, тие можат да се одвојат во два услова, од кои еден се нарекува теорема, а другиот реципроцитет. Така кога теоремата и нејзиниот реципроцитет се вистинити, тогаш имаме двоуслов. Од една едноставна теорема произлегува импликација чиј претходник е хипотеза и чиј следственик е теза на таа теорема.
Се вели дека хипотезата е доволен услов за тезата, и дека тезата е неопходен услов хипотезата; т.е. доволно е хипотезата да биде вистинита за тезата да биде исто така вистинита; додека пак неопходно е тезата да биде вистинита за хипотезата да биде исто така вистинита. Кога една теорема и нејзиниот реципроцитет се вистинити, велиме дека нејзината хипотеза е неопходен и доволен услов за тезата; т.е. дека истовремено е и причинител и последица.
Дефиниција
[уреди | уреди извор]Логичка еднаквост (двоуслов) е операција со две логички вредности, најчесто вредностите на два исказа, којашто дава вредност вистина ако и само ако обата оператори се невистинити или обата се вистинити.
Таблица на вистинитост
[уреди | уреди извор]Таблицата на вистинитост за p ↔ q е следнава:
| p | q | ≡ |
|---|---|---|
| т | т | т |
| т | ⊥ | ⊥ |
| ⊥ | т | ⊥ |
| ⊥ | ⊥ | т |
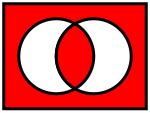
Венов дијаграм
[уреди | уреди извор]Веновиот дијаграм за „A ако и само ако B“ (црвените места се вистинити)
Својства
[уреди | уреди извор]- асоцијативност:
- комутативност:
- рефлексивност:
- запазување на вистинитост: Толкувањето според кое на сите променливи им се назначува вистинитосна вредност „вистина“ дава вистинитосна вредност „вистина“ како резултат на логичкиот двоуслов.
- линеарност
Правила на инференција
[уреди | уреди извор]Како и сите сврзници во логиката од прв ред, двоусловот има правила на инференција за негова примена во формални докази.
Двоусловен вовед
[уреди | уреди извор]Двоусловниот вовед ни овозможува да заклучиме дека, ако B следи од A, и A следи од B, тогаш A ако и само ако B.
На пример, од исказот „ако дишам, тогаш жив сум" и "ако сум жив, тогаш дишам“, може да се заклучи дека „Дишам ако и само ако сум жив“.
B → A A → B ∴ A ↔ B
Двоусловна елиминација
[уреди | уреди извор]Двоусловната елиминација ни овозможува да го изведеме условот од еден двоуслов: ако ( A ↔ B ) е вистина, тогаш можеме да заклучиме една насока на двоусловот, ( A → B ) и ( B → A ).
На пример, ако е вистина дека дишам ако и само ако сум жив, тогаш вистина е дека ако дишам, жив сум; така вистина е дека ако сум жив, дишам.
Формално претставено:
( A ↔ B ) ∴ ( A → B )
исто така
( A ↔ B ) ∴ ( B → A )
Белешки
[уреди | уреди извор]- ↑ Handbook of Logic, стр. 81
Наводи
[уреди | уреди извор]Brennan, Joseph G. Handbook of Logic, Второ издание. Harper & Row. 1961
Поврзано
[уреди | уреди извор]- Ако и само ако
- Логичка еквиваленција
- Логичка еднаквост
- ЕКСИЛИ порта
- Двоусловна елиминација
- Двоусловен вовед
Оваа статија содржи материјал од Biconditional на PlanetMath, кој е под ГЛСД лиценца.