Црвоточина
Оваа статија или заглавие има потреба од викифицирање за да ги исполни стандардите за квалитет на Википедија. Ве молиме помогнете во подобрувањето на оваа статија со соодветни внатрешни врски. |
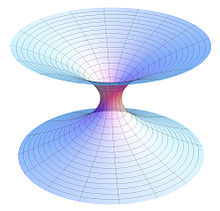
Црвоточина (или црвја дупка) — претставува хипотетичко тополошко обележје на време-просторот, коешто всушност претставува скратен пат низ времето и просторот. За поедноставено визуелно претставување на црвоточината, замислете го време-просторот како дводимензионална рамна површина (погледнете ја илустрацијата од десната страна). Доколку оваа површина се превитка на пола во 3 димензии, ни овозможува да си претставиме “мост” од црвоточина. (Ве молиме имајте предвид дека оваа слика е само визуализација прикажана за да се покаже во суштина незамислива структура која постои во 4 или повеќе димензии. Деловите на црвоточината може да бидат повисоки димензионални анлогии од деловите на превитканата дводимензионална површина; како на пример, наместо усти коишто се кружни форми во дводимензионалната рамнина, кај вистинската црвоточина, устите може да бидат сфери во тридимензионална површина). Црвоточината, теоретски, повеќе наликува на тунел со два краја секој на различна зафатнина и место во време – просторот. Не постојат видливи докази за постоењето на црвоточините, меѓутоа теоретски гледано постојат валидни солуции, кај равенката теорија на релативноста, којашто ги вклучува и црвоточините. Првиот вид на црвоточина како решение коешто беше откриено беше црвоточината Шварцчајлд којашто е претставена во Шварцчајлд метричкиот систем, опишувајќи внатрешна црна дупка, но се осозна дека овој вид на црвоточина пребрзо би се распаднал, за било што да би можело да премине од едниот на другиот крај. Црвоточините кои всушност би можеле да се преминат, познати како траверзабилни (преминливи) црвоточини, би постоеле само доколку, егзотичната материја со густина од негативна енергија, би можела да се искористи за да ги стабилизира. (Многу Физичари, како на пример Стивен Хокинг, Кип Торн и др. Сметаат дека ефектот Касимир е доказ дека густините од негативна енергија се возможни во контекст на теоријата за релативитет, исто така и хипотезата за квантната пена, понекогаш се користи за да се сугерира дека мали црвоточини може да се создадат и да исчезнат спонтано на Планково ниво (субатомско) ниво. Исто така се претпоставува дека, доколку црвоточина, одржувана отворена, од страна на космичките жици со негативна маса, создадена некаде за време на големата експлозија (Биг Бенг), би можела да се развие до макроскопско ниво, преку космичка инфлација. Американскиот теоретски физичар Џон Архибалд Вилер за првпат го воведува терминот црвоточина во 1957, меѓутоа уште во 1921 година германскиот математичар Херман Вејл ја поставува теоријата за црвоточините, преку масовна анализа на енергијата во електромагнетното поле.
Овие анализи наведуваат на размислување за ситуации......... каде што има мрежен ток од сили во вид на линии, коешто топологистите го нарекуваат “рачка” на повеќекратно поврзан простор, а за што на физичарите можеби би требало да им се прости за поживописниот термин “црвоточина”.
Дефиниција[уреди | уреди извор]
Основниот концепт за црвоточина со внатрешен универзум, е дека тоа претставува компактен регион на време – просторот, чија граница е тополошки безначајна, меѓутоа чива внатрешност не е едноставно поврзана. Формализирајќи ја ова идеја води до дефиниција како на пример следнава, преземена од делото на Мет Висер - Лоренциски црвоточини.
Доколку време Минковскиевиот простор содржи компактен регион Ω и доколку топологијата на Ω е во облик Ω ~ R x Σ, каде што Σ е тројноразновиден во контекст на нетривијалната топологија, чија граница има топологија во облик dΣ ~ S2 И доколку, понатаму, хиперповршините Σ се налик на простори, тогаш регионот Ω содржи квазитрајна црвоточина со внатрешен универзум.
Карактеризирањето на црвоточините со внатрешен универзум е уште потешко. Како на пример, може да замислиме “бебе-универзум” поврзан со својот “родител” преку тесен “папок”. Некој можеби папокот би го гледал како грло на црвоточината, меѓутоа време просторот едноставно е поврзан. Поради оваа причина црвоточините се дефинираат геометриски, спротивно од топологијата, како регионина времепросоторот кој ја ограничува поединечната деформација на затворените површини. На пример во делото на Енрико Родриго – Физиката на Ѕвездените Порти, црвоточината вообичане со дефинира неформално како
Регион на времепросторот кој содржи “световна цевка” (временската еволуција на затворена површина), која не може постојано да се дерформира (намали) до световна линија (временската еволуција на точка).
Шварцчајлдови црвоточини[уреди | уреди извор]
Лоренциските црвоточини, познати уште како и Шварцчајлдови црвоточини или Ајнштајн-Розен мостови, се мостови помеѓу две просторни области, коишто може да бидат моделирани како вакуумски солуции на Ајнштајновите равенки за полиња, и коишто, досега се смета дека се внатрешни делови од максимално проширениот Шварцчајлд метрички систем, опишувајќи внатрешна црна дупка без полнеж и без ротација. “Максимално проширениот” се однесува на идејата дека времепросторот нема никакви “рабови”: За каква било траекторија на слободно-паѓачката честичка (следејќи го геодезикот) во времепросторот, би било возможно да се продолжи патеката произволно, далеку во иднината или минатото на честичката, доколку траекторијата не наиде на гравитациска сингуларност (бесконечно голема гравитација) како онаа во центарот на внатрешноста на црната дупка. Со цел да се задоволи ова барање (услов), излегува дека како додаток на внатрешниот регион на црната дупка, којшто честичките го преминуваат кога однадвор ќе навлезат во хоризонтот на настани, мора да постои регион со одвоена внатрешност - бела дупка, кој ни овозможува да ги издолжиме траекториите на кои, надворешниот набљудувач ги гледа како да се креваат надалеку од хоризонтот на настани. Исто како што има два одделни внатрешни региони на максимално проширениот времепростор, исто така постојат и два одделни надворешни региони, понекогаш нарекувани два различни “универзуми”, каде што вториот универзум ни овозможува да екстраполираме некои возможни траектории на честичките во двата внатрешни региони. Ова значи дека внатрешниот регион на црната дупка, може да содржи мешавина од честички кои упаднале и од двата универзуми ( и затоа набљудувачот кој упаднал од едниот универзум, можеби би можел да ја види светлината, која упаднала од другиот), а исто така честичките од вантрешниот регион – бела дупка може да избегаат и во двата универзума. Сите четири региони може да се видат во дијаграмот на времепросторот кој користи Крускал-Зекерес координати (координатен систем за Шварцчајлд геометријата за црните дупки), како што е дискутирано и илустрирано на страната бели дупки и црвоточини. Во овој времепростор, возможно е да се дојде до кординантни системи доколку се одбере една хиперповршина со константно време (множество од точки кои имаат иста временска координата, каде секоjа точка на површината има налик на просторна одвоеност, давајќи т.н. “лик на просторна површина”) и се црта “вметнувачки дијаграм”, каде што се исцртува кривата на просторот во тоа време (разгледај ја дискусијата за “вметнувачките дијаграми” на оваа страна), вметнувачкиот дијаграм ќе наликува како цевка која ги поврзува двата надворешни региони, позната како “Ајнштајн-Розен мост”. На пример разггледај ги дијаграмите на оваа страна кои покажуваат максимално проширена Шварцчајлд солуција со Крускал-Зекер координатите, заедно со белите хиперповршини на непроменливото време нацртани на (времето и во некои други координантни системи освен Круска-зекер координатите, затошто хиперповршината на константното време кај Крускал-Зекер, би изгледала како хоризонтална линија нацртана кога би била нацртана во Крускал-Зекер дијаграмот) одговарачкиот вметнувачки дијаграм за конкретната хиперповршина. Запамети дека Шварцчајлд метричкиот систем опишува идејализирана црна дупка којашто постои бесконечно од гледиште на надворешниот набљудувач; пореалистична црна дупка, која се создава во определено време, преку згаснувањето на една ѕвезда, би имала потреба од друг метрички систем. Кога ѕвездената паѓачка материја се вметнува во дијаграмот историја на црната дупка, таа го отстранува делот од дијаграмот кој одговара на внатрешниот регион-бела дупка, заедно со делот на дијаграмот којшто е определен за внатрешниот универзум. Ајнштајн-розен мостот е откриен од страна на Алберт Ајнштајн и неговиот колега Нејтан Розен, којшто и прв ги објави резултатите во 1935 г. Меѓутоа во 1962 Џон А. Вилер и Роберт Фулер издадоа документ преку кој изнесуваат дека овој вид на црна дупка е нестабилен, и дека ќе исчезне пребрзо за да може светлината (или било која друга честичка којшто се движи поспоро од светлината) која што паѓа од еден внатрешен регион, да стигне до другиот внатрешен регион. Уште пред да станат очигледни проблемите во стабилноста на Шварцчајлд цврјите дупки, се сметаше дека квазарите се белите дупки кои го офрмуваат крајот на црвоточините од овој вид. Иако Шварцчајлд црвоточините не се трверзабилни(преминливи), нивното постоење го инспирираше Кип торн да замисли преминливи (траверзабилни) црвоточини создадени задржувајќи го “грлото” од Шварцчајлдовиот модел за црвоточини, отворени со екзотична материја (материја која има негативна маса/енергија).
Преминливи црвоточини[уреди | уреди извор]
Лоренцовите преминливи (траверзабилни) црвоточини би овозможиле патување од еден дел на универзумот до друг дел во истиот универзум премногу бргу, или би овозможиле патување од еден кон друг универзум. Возможноста за постоење на траверзабилни црвоточини во теоријата за релативноста беше за првпат демонстрирана од страна на Кип торн и неговиот дипломиран студент Мајк Морис во весник 1988год. И поради таа причина, видот на траверзабилната црвоточина која тие ја прикажаа, одржувана отворена од страна на сферична школка од егзотична материја, се нарекува Морис-Торн црвоточина. Подоцна други видови на траверзабилни црвоточини беа прикажани како возможни решенија под капата на равенките од теоријата за релативитет, вклучувајќи и разновидни видови анализирани преку весник во 1989 г. од страна на Мет Висер, каде што може да биде направена преминлива патека низ црвоточината, меѓутоа патеката не треба да преминува низ регионот со егзотична материја.
Меѓутоа во Гос – Бонет теоријата (модификација на теоријата за релативитет вклучувајќи дополнителни специјални димензии кои понекогаш се изучуваат во контекстот на мембранската космологија) егзотичната материја не е клучна за да постојат црвоточините – тие може да постојат дури и без материја. Видот на црвоточините одржувани отворени со помош на космички конци (мембрани) со негативна маса беше презентиран од срана на Висер во соработка со Крамер, каде што беше прикажано дека таквите црвоточини би можеле природно да се создадат во раниот универзум. Црвоточините поврзуваат две точки во времепросторот, што во принцип значи дека би овозможиле и патување низ времето, а исто така и низ просторот. Во 1988, Морис, Торн и Јуртсевер експлицитно работеа на тематиката како да преобразат црвоточина која овозможува патување низ простор, во црвоточина која овозможува патување низ време. Меѓутоа, според теоријата за релативитет, не би било возможно да искористиш црвоточина да се вратиш во времето назад, порано од времето кога црвоточината била за првпат преобразена во временска машина, забрзувајќи една од нејзините две усти.
Рејчодуриевата теорема и егзотичната материја=[уреди | уреди извор]
За да се разбере зошто е потребна егзотична материја, замислете пристигачка светлина патувајќи во правецот на геодезикот, а потоа ја преминува црвоточината и се издолжува на другата страна. Издолжувањето оди од негативитет кон позитивитет. Затоа што вратот на црвоточината има конечна големина, не би очекувале нејзиното каустично средство да се развие, не барем во близината на вратот. Според оптичка Рејчодуриева тероема за ова е потребно прекршување на просечната нулта енергетска состојба. Квантнинте ефекти како на пример Касимир ефектот, неможат да ја нарушат просечната нулта енергетска состојба во било кој соседен просто со нулта прекршување, но пресметките во полукласичната гравитација налагаат дека квантните ефекти можеби можат да ги нарушат овие состојби во извитоперениот времепростор. Дури и да можат, можеби квантните ефекти неможат да нарушат послаба состојба позната како”акронално просечна нулта енергетска состојба” , а ова може да ја отфрли возможноста за траверзабилни црвоточини.
Побрзо патување од светлината[уреди | уреди извор]
Невозможноста за патување со поголема брзина од светлината се аплицира само локално. Црвоточините овозможуваат суперлуминално/суперсветлинско (побрзо од светлината) патување осигурувајќи дека брзината на светлината не е надмината локално во било кое време. Патувајќи низ црвоточина сублуминални/субсветлински (побавни од светлината) брзини се применуваат. Доколку се поврзнаи две точки преку црвоточина, времето коешто е потребно да се премине дупката, ќе биде помало од времето коешто му е потребен на светлосниот зрак за да го помине просторот надвор од црвоточината. Како и да е, светлосен зрак кој патува низ црвоточина, секогаш ќе го победи патникот. Како аналогија, трчајќи по страната на планината со максимална брзина ќе трае подолго отколку да пешачиш по ископаниот тунел.
Патување низ времето[уреди | уреди извор]
Теоријата за релативитет предлага дека, доколку постојат траверзабилни црвоточини, тие можат да овозможат патување низ времето. Ова би се постигнало преку забрзување на едниот крај од црвоточината на поголема брзина во однос на другиот, и во даден интервал подоцна, враќање на првобитната брзина (релативистичка временска дилатација), како резултат забрзаната уста од црвоточината би стареела помалку од стационарната видлива за нбљудувачот, слично на она што е прикажано во близначкиот парадокс. Меѓутоа, времето се поврзува рзлично во црвоточината од времето надвор од неа, па така синхроизираните часовници ќе останат синхронизирани за оној кој патува низ црвоточината, без разлика како се движат нејзините усти. Ова значи дека секој што влегол преку забрзаната уста на црвоточината, ќе излезе преку стационарната во момент од времето пред неговиот влез. На пример, замислетен два часовника на двете усти и двата ја покажуваат годината 2000. По патувањето со релативистични брзини, забрзаната уста се враќа на истиот регион како стационарната уста, каде што часовникот кај забрзаната уста покажува 2005 додека кај стационарната покажува 2010. Патникот кој влегол преку збарзаната уста, во овој момент, ќе излезе преку стационарната, каде што неговиот часовник исто покажува 2005, во истиот регион, меѓутоа 5 години во минатото. Таква конфигурација на црвоточините би им овозможила на чесичките да оформат затворен вртлок во времепросторот познат како затворена временска крива. Се смета дека не е возможно црвоточината да се преобрази во временска машина на овој начин, претпоставките се направени во контекст на теоријата за релитивитет, меѓутоа оваа теорија не ги вклучува квантните ефекти. Некои анализи кои се служат со полукласичниот пристап за да ги вметнат класичните ефекти во теоријата за релативитет индицираат дека повратен јазол од виртуелни честички би циркулирал низ црвоточината со постојано зголемувачки интензитет, уништувајќи ја уште пред каква било информација да премине преку неа содествувајќи со хронолошки заштитничката претпоставка. Ова беше доведено до прашање поради претпоставката за распрснувачко зрачење при патувањето низ црвоточина, затоа е спречена бесконечна акумулација. Дебатата за оваа тематика е опишана од страна на Кип С. Торн во книгата Црни дупки и временски витли, а постручна дискусија може да се најде во Квантната физика на Хронолошка протекција од Мет Визер. Ито така тука е и Римскиот прстен, којшто претставува конфигурација од повеќе црвоточини. Овој прстен најверојатно овозможува затворена временска јамка со стабилни црвоточини кои се анализирани преки полукласичната гравитација, иако без целосна теорија за квантната гравитација непотврдено е дали полукласичниот пристап е доверлив во конкретниов случај.
Метрички системи[уреди | уреди извор]
Теориите за метричките системи на црвоточините ја опишуваат геометријата на времепросторот и служат како теориски модели за патување низ времето.
Во фантастиката[уреди | уреди извор]
Црвоточините се чести елементи во научната фантастика и дозволуваат меѓуѕвездено (понекогаши меѓувселенско) патување во човечки временски периоди.
|

