Хи-квадратна распределба
Во теоријата за веројатност и статистиката, хи-квадратна распределба со υ степени на слобода е распределба на збирот од квадратите на n независни нормални случајни променливи. Тоа е еден од најшироко употребуваните распределби на веројатност во дедуктивната статистика, на пример, во проверка на хипотези или во донесување заклучок за интервалите на доверба. Хи-квадратната распределба е посебен случај на гама-распределбата, и уште се нарекува Пирсонова распределба и централен хи-квадратна распределба.[1][2]
Дефиниција[уреди | уреди извор]
Ако x1,x2……,xn се независни, стандардни, нормални променливи, тогаш збирот на нивните квадрати е распределен според хи-квадратната распределба со υ степени на слобода.[3]
Врската меѓу варијансата на примерокот со таа на популацијата е прикажана во χ2. Соодносот помеѓу варијансата на примерокот (S2) помножен со n-1, и варијансата на популацијата (σ2) е распределбата χ2, ако популацијата од која се извлечени вредностите има нормална распределба.[4]
Особености[уреди | уреди извор]
Ако примерокот е добиен од нормална распределба, вредноста во заградите е всушност z-вредност. Така χ2 е збир на квадрираните z-вредности.[5]
Доколку одблиску се разгледа формулата:
1. Прво, оваа распределба не може да има вредност помала од 0. Тоа е така бидејќи s2 и σ2 се квадрирани и големината на примерокот е позитивен интеграл. Оттаму, опсегот на било која променлива на хи-квадрат е од 0 до, теоретски, бесконечност.
2. Средината на хи-квадратна распределба е едноставно n-1, бројот на степени на слобода.
3. Формата на оваа распределба е дефинитивно асиметрична. Поради тоа што опсегот е ограничен на левата страна со 0 и неограничен на десната страна, неговата форма е искривена надесно. Искривеноста е значителна кога бројот на степени на слобода е мал, но истата се намалува како што степените на слобода се зголемуваат.[6]
4. Коефициент на асиметрија:
Распределбата е асиметрична. За υ -> ∞ распределбата станува симетрична.
5. Коефициент на сплоснатост:
За υ -> ∞ распооредот ја достигнува нормалната висина.[7]
Определување на степените на слобода[уреди | уреди извор]
-
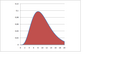
Функции за густината на веројатноста за хи-квадратната распределба со 1,4,8 и 12 степени на слобода (υ)
Распределбата е дефинирана само за позитивни вредности, бидејќи варијансите се сите позитивни вредности. Пример за функција на густина на веројатност е покажан во горниот графикон. Функцијата на густина е асиметрична со издолжена позитивна опашка. Можеме да карактеризираме одреден член од фамилијата на хи-квадратни распределби со единствен параметар познат како степени на слобода, означен со υ. Хи-квадратната распределба со υ степени на слобода ќе се означува како χ2υ. Средината и варијансата на оваа распределба се еднакви на бројот на степени на слобода и на двапати по бројот на степени на слобода.
Е(χ2υ) = υ и Var (χ2υ) = 2υ
Со користење на овие резултати за средината на варијансата на хи-квадратната распределба, наоѓаме дека:
-
Изведување на формула за варијанса на хи-квадратната распределба
А за да ја добиеме варијансата на s на квадрат имаме:
Можеме да ги користиме својствата за да ја најдеме варијансата на распределбата на примерокот за варијансата на примерокот кога матичната популација е нормална. Параметарот υ на хи-квадратната распределба се нарекува степени на слобода. За да помогнеме да се разбере концептот на степени на слобода, прво земете дека варијансата на примерокот е збир на квадратите на n вредности од обликот (xi - x̅)2. Овие n вредности не се независни бидејќи нивниот збир е нула. Оттука ако знаеме n-1 од вредностите (xi - x̅)2 :
Бидејќи можеме да ја одредиме n-тата големина ако ги знаеме преостанатите n-1 големини, велиме дека има n-1 степени на слобода – независни вредности – за пресметување на s2. Во спротивно, ако µ беше непозната, можевме да ја пресметаме оценетата вредност на σ2 со користење на големините (x1 – M), (x2 – M), … , (xn – M) при што секоја од нив е независна. Во тој случај би имале n степени на слобода од n независни опсервации на примерокот, xi. Меѓутоа М не е позната и мораме да ја користиме нејзината оценета вредност за да ја пресметаме оценката на σ2. Како резултат на тоа, еден степен на слобода е изгубен во пресметување на средината на примерокот, и имаме n-1 степени на слобода за s2.
Наоѓање на вредностите на хи-квадратната распределба[уреди | уреди извор]
За многу примени кои ја вклучуваат варијансата на популацијата треба да ги најдеме вредностите на кумулативната распределба на χ2, особено горните и долните опашки на распределбата. На пример:
P( x̅210) < K) = 0.05
P( x̅210) > K) = 0.05
За оваа цел, табеларно е прикажана распределбата на χ2 случајната променлива во таблицата. Во оваа таблица степените на слобода се дадени во левата колона, а критичните вредности за υ за различни нивоа на веројатност се означени во другите колони.
Така, за 10 степени на слобода, вредноста за долниот интервал е 3,94. Овој резултат е добиен со одење до редот 10 степени на слобода во левата колона и потоа со читање до колоната со наслов веројатност 0,950 на десно од влезовите на овие колони. χ2 вредноста е 3,94. Слично на тоа, за горниот 0,05 интервал, вредноста на К е 18,31. Овој резултат е добиен со одење до редот 10 степени на слобода во левата колона и потоа со читање до колоната со наслов веројатност 0,50 на десно од влезовите на овие колони. χ2 вредноста е 18,31.
P( x̅210) < 3,94) = 0.05
P( x̅210) < 18,31) = 0.05[8]
-
Позицијата на алфа кај Хи-квадрат
Донесување заклучок[уреди | уреди извор]
Со оглед на тоа дека има многу статистички ситуации каде распределбата на популацијата јасно не е нормална, употребата на χ2 распределбата за да се донесат заклучоци за σ2 (или индиректно за σ) во вакви случаи е несоодветна. Како резултат на ова, нашата способност да донесуваме заклучоци за популацијата или варијансата може да биде сериозно ограничена. Како може да се определи дали употребата на овој метод е соодветна? Добра идеја е се направи хистограм на примерокот, ако примерокот е доволно голем за да овозможи значајни информации. Ако хистограмот очигледно не е нормален ( ако е значајно искривен), тогаш овој хи-квадрат метод треба да се избегне. Ако примерокот е премал за да овозможи значајни информации, мора да се потпреме на субјективната проценка заснована на нашето личното познавање за распределбата на популацијата.[9]
Примена[уреди | уреди извор]
χ2-распределбата, како и секоја друга распределба, објаснува како случајната променлива се однесува. Таа кажува кои се најверојатните вредности на случајната променлива (каде има најмногу простор под кривата), и кои се најмалку веројатните вредности на случајната променлива (каде има најмалку простор под кривата).[10]
Хи-квадратната распределба е употребуван во повеќето статистички софтверски пакети, главно затоа што можат да се претставуваат табеларно.[9]
Најмногу се користи во областа на непараметарските тестови односно кај Хи-квадрат тестот. Всушност се применува за испитување на значајноста на разликите помеѓу емпириските и теоретските честоти, односно помеѓу стварните и теоретските вредностина еден или повеќе белези.[7]
Понекогаш во статистичките анализи, истражувачот е повеќе заинтересиран за варијансата на популацијата отколку средината на популацијата или пропорцијата на популацијата. На пример, на снабдувачите кои сакаат да стекнат повисок статус во својата работа или оние кои сакаат да ги задржат договорите со своите купувачи,често им се бара да ја прикажат редукцијата на варијацијата на деловите со кои ги снабдуваат клиентите. Тестовите се спроведени врз примероци со цел да се утврди големината на варијацијата и да се определи дали се исполнуваат целите кога станува збор за намалување на варијабилитетот.
Проценувањето на варијацијата е важно во многу различни ситуации во бизнисот. На пример, варијациите меѓу читањата кај авионскиот висиномер мора да бидат минимални. Не е доволно да се знае дека, просечно, определен бренд на висиномер ја прикажува вистинската надморска височина. Исто така, важно е разликата меѓу инструментите да биде мала. Така што, мерењето на варијацијата на висинометарот е критично. Деловите кои се вградуваат во моторите мора точно да се вклопуваат константно. Широкиот варијабилитет меѓу деловите може да резултира со дел кој е премногу голем за да го собере или да е премногу мал што ќе резултира со преголема толеранција, што предизвикува вибрации.[4]
Наводи[уреди | уреди извор]
- ↑ Милтон Абрамовиц; Ирене А. Стегун - Прирачник за математички функции со форули, графици и табели (1965)
- ↑ Н. Л. Џонсон; С.Коц; Н. Балакришнан - Непрекинати едноваријантни распределби (1994)
- ↑ Александер Муд; Френлин А. Грејбил, Дуан К. Боес - Вовед во стастистичката теорија(1974)
- ↑ 4,0 4,1 Кен Блек – Бизнис статистика за современо донесување одлуки(2008)
- ↑ Дејвид Е. Гробнер, Патрик В. Шенон, Филип К. Фрај, Кент Д. Смит -Бизнис статистика од аспект на донесување одлуки
- ↑ Џорџ К. Канавос, Дон М. Милер – Вовед во модерната бизнис статистика(1993)
- ↑ 7,0 7,1 Славе Ристески и Драган Тевдовски – Статистика за бизнис и економија(2010)
- ↑ Пол Њуболд, Вилијам Л. Карлсон, Бети Торн - Статистика
- ↑ 9,0 9,1 Џорџ К. Канавос, Дон М. Милер – Вовед во модерната бизнис статистика(1993)
- ↑ Мерлин К. Пелоси, Тереза М. Сандифер - Правење бизнис статистика со Excel; податоци, постапка и донесување одлуки