Полуправа

Полуправа како дел од права

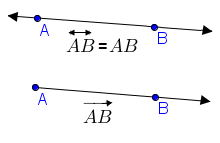
Во геометријата, полуправа (зрак) се опишува како дел од права кој започнува во една точка од правата и продолжува непрекинато по правата во една од двете насоки кои таа точка ги определува.^[1]^[2]^[3]

Во Евклидовата геометрија, за две различни точки А и В, постои една единствена полуправа со почетна точка А, која поминува низ B (па потоа продолжува бескрајно во таа насока). Истата се означува со $AB$ , а поретко и со $A{\overrightarrow {B}}$ или $[A{B})$ .
Полуправата е еднодимензионален објект, т.е. има должина, но нема ниту ширина ниту висина.
Полуправата има само една крајна точка (теме кое се смета за почеток), па затоа нема одредена должина, односно има бескрајна должина.

Забелешки[уреди | уреди извор]

Најчесто се користи поимот полуправа во следниве објаснувања.

Секоја точка А на една права ја дели правата во две полуправи.
Нека А и В се две различни точки. Пресекот на полуправите $[A{B})$ и $[BA)$ е отсечката ${\overline {AB}}$ .
Две посебни полуправи $[AB)$ и $[AC)$ со иста почетна точка определуваат агол.
Бројна оска е (единствената) права во еднодимензионален реален простор, а секоја полуправа на неа е решение на линеарна неравенка со една непозната. (На пример, неравенката $x>3$ геометриски се претставува со отворена полуправа која почнува во $x=3$ и продолжува бескрајно надесно.)

Параметарски облик на полуправа во тридимензионален простор[уреди | уреди извор]

Нека се дадени две точки $A(x_{1},y_{1},z_{1}),B(x_{2},y_{2},z_{2})\in \mathbb {R} ^{3}$ . Параметарскиот облик на полуправата со почеток во А, и која поминува низ В е ограничување на параметарскиот облик на правата низ А и В за $t\in [0,+\infty )$ , односно

   $\left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a}t}\\{y(t)={y_{1}}+{b}t}\\{z(t)={z_{1}}+{c}t}\end{array}}\right.$  каде  ${a=(x_{2}-x_{1})},\,{b=(y_{2}-y_{1})},\,{c=(z_{2}-z_{1})}$  ,    $t\in [0,\infty )$  .