Механичка рамнотежа
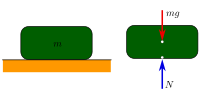
Во класичната механика, честичката е во механичка рамнотежа ако нето силата на честичките е нула. Со проширувањето, физички систем направен од многу делови е во механичка рамнотежа ако нето силата на секоја од поединечните делови е нула.:45–46
При дефинирање на механичка рамнотежа во оглед на силата, постојат многу различни дефиниции за механичка рамнотежа кои се сите математички еквиваленти. Во однос на импулсот, систем е во рамнотежа доколку динамиката на нејзините делови е константа. Во однос на брзината, системот е во рамнотежа доколку брзина е константна. Во вртежна механичка рамнотежа, аголниот импулс на објектот е конзервиран и нето вртежниот момент е нула.[1] генерално во конзервативни системи, рамнотежа се воспоставува во точката при конфигурацијата на просторот каде зголемувањето на потенцијална енергија во однос на генерализираните координати е нула.
Ако честичката во рамнотежа има брзина нула, тогаш честичката е во статична рамнотежа.[2][3] Ако сите честички во рамнотежа имаат константна брзина, тогаш е секогаш можно да се најде инертна референтна рамка во која честичката е неподвижна, со оглед на рамката.
Стабилност[уреди | уреди извор]
Важна одлика на системите во механичка рамнотежа е нивната стабилност.
Тест на потенцијална стабилност на енергија[уреди | уреди извор]
Ако имаме функција која го опишува потенцијалната енергија на системот, ние може да ја утврдиме рамнотежата на системот со користење на калкулус. Системот е во машинска рамнотежа на критичните точки од функцијата со опишување на потенцијалната енергија на системот. Ние може да ги лоцираме овие точки користејќи го фактот дека дериватот на функцијата е нула во овие точки. За да се утврди дали системот е стабилен или нестабилен, ќе го примениме вториот дериватен тест:

- Вториот дериват < 0: Потенцијалната енергија е во локален максимум, што значи дека системот се наоѓа во нестабилна рамнотежа. Ако системот е преместен на произволно мала оддалеченост од урамнотежената состојба, силите на системот ќе предизвикаат таа да се движи дури и подалеку.

- Вториот дериват > 0: Потенцијалната енергија е на локален минимум. Ова е стабилна рамнотежа. Ако повеќе од една состојба на стабилна рамнотежа е можна во еден систем, било која рамнотежа чија потенцијална енергија е поголема од апсолутниот минимум претставува метастабилна состојба.

- Вториот дериват = 0 или не постои: состојбата е неутрална и речиси останува во рамнотежа доколку се помести за мала количина. Да се испита прецизно стабилноста на системот, повисок ред деривати кои мораат да се испитаат. Состојбата е нестабилна ако најнискиот дериват ( ≠ 0 ) е негативен и прост, а стабилен ако најнискиот дериват ( ≠ 0 ) има позитивна вредност и е сложен, и неутрални ако сите повисоки деривати се нула. Во вистински неутрална состојба на енергија не се менува и состојбата на рамнотежа има определена големина. Ова понекогаш се нарекува како состојба која е маргинално стабилна.
Кога станува збор за повеќе од една димензија, можно е да се добијат различни резултати во различни правци, на пример стабилност во однос на преместувања во x-насока, но нестабилност во y-насока, случај познат како точка на седло. Генерално рамнотежа е стабилна ако таа е стабилна во сите правци.
Статистички неопределен систем[уреди | уреди извор]
Понекогаш нема доволно информации во врска со силите кои дејствуваат на телото за да се одреди ако тоа е во рамнотежа или не. Ова го прави статистички неопределен систем.
Примери[уреди | уреди извор]
Пример за механичка ранотежа кај тело во мирување е статична рамнотежа. Минималниот број на статични рамнотежи на конвексни тела ( мирување на тело на хоризонтална подлога со помош на гравитациска сила) е најважно. Во овој случај, минималниот број е 4, додека пак во 3 димензии може да се изгади тело со само една стабилна и една нестабилна рамнотежна точка, ова се нарекува гомбок.
Пример за механичка рамнотежа е човек кој притиска на федер. Тој може да го притисне додека не дојде во состојба каде што реактивната сила на федерот и силата која се соопштува врз федерот е еднаква, тогаш човекот нема да може да ја притисне уше повеќе. Во оваа состојба системот ќе биде во механичка рамнотежа. Кога силата на притискање ќе се намали федерот се враќа во својата првобитна состојба.
Забелешки и препораки[уреди | уреди извор]
- ↑ Beer FP, Johnston ER, Mazurek DF, Cornell PJ, and Eisenberg, ER (2009). Vector Mechanics for Engineers: Statics and Dynamics (9. изд.). McGraw-Hill. стр. 158.CS1-одржување: повеќе имиња: список на автори (link)
- ↑ Herbert Charles Corben & Philip Stehle (1994). Classical Mechanics (Reprint of 1960 second. изд.). Courier Dover Publications. стр. 113. ISBN 0-486-68063-0. Укажано повеќе од еден
|ISBN=и|isbn=(help) - ↑ Lakshmana C. Rao; J. Lakshminarasimhan; Raju Sethuraman; Srinivasan M. Sivakumar (2004). Engineering Mechanics. PHI Learning Pvt. Ltd. стр. 6. ISBN 81-203-2189-8. Укажано повеќе од еден
|ISBN=и|isbn=(help)
