Аналитичка геометрија

Аналитичка геометрија — дел од геометријата кој користи негеометриски методи за решавање на геометриски проблеми (задачи). Иако и стандардната геометрија користи аритметички (пресметковни) методи за решавање на проблемите, сепак, во аналитичката геометрија нивното разгледување се врши на поемпириски и поапстрактен начин, каде на одредена геометриска појава ѝ одговата соодветен систем равенки (кој пак може да брои и една равенка). Апаратот и методите со кои се служи аналитичката геометрија се разновидни, така што таа пред сè има допирни точки со математичката анализа и со линеарната алгебра, а директно е поврзана и со останатите гранки на геометријата (диференцијална, проективна и др.)
Основни поими и поделба[уреди | уреди извор]
Важен напредок се постигнува во 19. век со проиширувањето на поимот простор, односно разгледувањето на т.н. произволни простори во кои она што сетилно се наметнува како „правост“ (не-кривост, рамномерност, унифицираност) на еден простор не е исполнето, т.е. се разгледуваат простори кои не се Евклидови. Особен придонес за развој на оваа теорја имаат математичарите Бернхард Риман, Николај Лобачевски и Јанош Бојаи.
Иако има допирни точки со повеќе математички дисциплини, аналитичката геометрија има генерално независен пристап кон проблемите (што значи дека треба да се вложи повеќе труд за добро да се совлада). Модерниот пристап на ова поле пак, се потпира главно на линеарната алгебра и бара нејзини широки познавања, и, иако помалку чуден, дава подобра основа во совладувањето и надградбата на материјалот.
Според просторот во кој се разработуваат проблемите (задачите) аналитичката геометрија на евклисдите простори условно може да се подели на:
- аналитичка геометрија во рамнина (во 2Д) (под рамнина се подразбира дводимензионална рамнина од тридимензионалниот простор);
- аналитичка геометрија во простор (во 3Д) (потпростор се подразбира тридимензионалниот Евклидов простор);
- аналитичка геометрија во nD (односно разгледување на геометриски појави во простори со произволен број димензии)
Првите две гранки на аналитичката геометрија се поконкретни и поексплицитни, а со тоа и појасни и разбирливи, додека третата гранка е апстрактна, што поради бројот на димензии, што поради сè поголемиот удел на линеарната алгебра.
Аналитичка геометрија во Евклидови простори[уреди | уреди извор]
Секој n-димензионален простор се нарекува Евклидов ако во него може да се дефинира скаларен производ на два произволни вектори од просторот. Евклидовите простори се релативно лесни за разгледување и разработување без разлика на нивната димензионалност, бидејќи претставуваат логичка надградба на дво- и тридимензионалниот простор (кои исто така се Евклидов); Токму рамнинската (дводимензионална) аналитичка геометрија и просторната (тридимензионална) аналитичка геометрија се основните случаи со кои се занимава оваа гранка од математиката бидејќи се работи за сетилно пристапни случаи. Само да напоменеме, бидејќи Евклидовиот простор е во основа векторски простор, тој не мора да е реален, туку може да е и комплексен (точките да имаат и комплексни координати).
Рамнинска (2Д) аналитичка геометрија[уреди | уреди извор]
Овој дел се занимава со разработување и апстрактна дискусија на геометриските фигури во рамките на една рамнина. Тука пред сè се разгледуваат правите (разни начини на нивно претставување и значење на одредени елементи во рамките на едно претставување) и кривите од втор ред (кружница, елипса, парабола, хипербола) како и заемната положба помеѓу правите од една и кривите од втор ред од друга страна (т.е. опишување на тангенти, нормали, секанти).
Равенки на права во рамнина[уреди | уреди извор]
Правата во рамнина може да се претстави како график на линеарна функција. Иако постојат повеќе начини на претставување на правата како множество точки кои задоволуваат одредено равенство, заедничко за сите нив е тоа што во основа сите зависат од „правецот“ или градиентот на правата; под правец ќе го подразбираме аголот кој правата го зафаќа со позитивниот дел на -оската. Правата обично се бележи со мало латинско .
Експлицитен облик на равенка на права е всушност претставување на правата како график на линеарна функција. Тој се задава на следниов начин:
каде е коефициент на правец на правата дефиниран како , е аголот што го зафаќа правата со позитивниот дел на -оската, додека e отсечок што правата го отсекува на -оската.
Имплицитен облик на равенка на права е претставување на точките од правата како решенија на линеарна равенка со две непознати: и , т.е. равенка од облик:
Јасно, може да се направи „премин“ од имплицитен на експлицитен облик на равенката на права, ако последната равенка ја запишеме како:
Сегментен облик на равенка на права е претставување на правата преку отсечоците што таа ги отсекува на координатните оски (кај експлицитниот облик се користеше само отсечокот на -оската). Ако на -оската правата отсекува дел со должина , а на -оската дел со должина , тогаш правата може да се запише како равенка од облик:
Равенка на права низ една и низ две точки. ако е познат градиентот на правата: и координатите на барем една точка која лежи на правата: , тогаш правата може да се претстави преку следнава равенка:
Доколку, пак, се познати две точки коишто лежат на правата: и , тогаш правата може да се претстави со равенката:
каде со изразот е определен градиентот на правата.
Равенка на кружница[уреди | уреди извор]
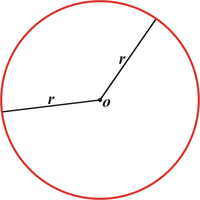
За разлика од правата каде зависноста на координатите на точките е линеарна, кај кружницата таа е квадратна. Слично како и за правата, и за кружницата постојат неколку начини на изразување на оваа зависност. Кружницата обично се бележи со мало латинско .
Централна равенка на кружница ја претставува кружницата со центар во координатниот почеток: која има полупречник . Таа е од облик:
Општа равенка на кружница ја претставува кружницата со центар во точка и полупречник и е од облик:
Доколку ги квадрираме изразите во последното равенство, се добива:
Ако формално запишеме:
тогаш добиваме дека кружницата може да се претстави со равенката:
Обратно, кружницата може да биде зададена токму како квадратна равенка со две непознати, од облик:
Тогаш координатите на центарот и полупречникот ги определуваме како:
Растојание меѓу две точки[уреди | уреди извор]
Равенка на елипса[уреди | уреди извор]
Равенка на хипербола[уреди | уреди извор]
Равенка на парабола[уреди | уреди извор]
Просторна (3D) аналитичка геометрија[уреди | уреди извор]
Во овој дел се разгледуваат и дискутираат на поапстрактен начин и геометриските фигури (како на пример, прави, кружници итн.) и геометриските тела (рамнина, топка, елипсоид, параболоид, хиперболоид итн) во просторот. Тука спаѓаат и специјалните случаи (тангента на просторно тело, тангенцијална рамнина на просторно тело и слично.)
Равенки на права во простор[уреди | уреди извор]
Равенки на рамнина во простор[уреди | уреди извор]
Околу повеќедимензионалната (nD) аналитичка геометрија[уреди | уреди извор]
Во повеќе од тридимензионални простори (кои се сетилно непристапни), се врши обопштување на поимите од претходно споменатите случаи (слично како што поимот топка е обопштување на поимот кружница од две, на три димензии). Тогаш наведените случаи се разгледуваат како потпростори од разгледуваниот простор (кој секако е векторски простор!), а во што се вклучува опсежен апарат кој е несвојствен за 2D и 3D аналитичката геометрија, а кој припаѓа на линеарната алгебра.
|




































