Централен агол

Централен агол
	Централен агол Θ има теме во центар O на кружницата
Тип	агол во рамнина (2д)
Поддршка	кружница

Нека е дадена кружница. Централен агол e агол чиe теме е центарот О на кружницата, а чии краци се два дистинктни полупречници.^[1] При опис или цртање на централен агол, покрај обележувањето на краците-полупречниците, т.е. пресечните точките А и В, децидно треба да се обележи дали се мисли на конвексниот (<180°) или неиспакнатиот агол (>180°).

Централен агол Θ е: 0° < Θ < 360° односно 0 < Θ < 2π (радијани)

Формули[уреди | уреди извор]


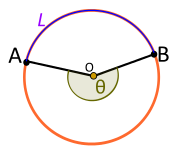
Сл.1: Централен агол. Конвексен (го зафаќа пократкиот лак L).

Ако пресечните точки А и В на краците со кружницата формираат пречник, тогаш Θ = 180° и е рамен агол. (Во радијани, Θ = π.)

Нека L е пократкиот лак помеѓу А и В, а R нека е полупречникот на кружницата.^[2]

Ако централниот агол Θ го зафаќа L (види сл.1), тогаш

 $0^{\circ }<\Theta <180^{\circ }\,,\,\,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }={\frac {L}{R}}$

Доказ (со степени): Периметарот на кружница со полупречник R e: 2Rπ, а лакот L е (^Θ/_360°) пропорционален дел од целиот периметар (види лак (кружница)). Значи:

L={\frac {\Theta }{360^{\circ }}}\cdot 2R\pi \,\Rightarrow \,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }


Сл.2: Централен агол. Неиспакнат (не го зафаќа пократкиот лак L).

Доказ (со радијани): Периметарот на кружница со полупречник R e: 2Rπ, а лакот L е (^Θ/_2π) пропорционален дел од целиот периметар (види лак (кружница)). Значи:

L={\frac {\Theta }{2\pi }}\cdot 2R\pi \,\Rightarrow \,\Theta ={\frac {L}{R}}

Ако централниот агол Θ не го зафаќа L, тогаш тој е неиспакнат агол (види сл.2) односно:

 $180^{\circ }<\Theta <360^{\circ }\,,\,\,\Theta =\left(360-{\frac {180L}{\pi R}}\right)^{\circ }=2\pi -{\frac {L}{R}}$

Наводи[уреди | уреди извор]

↑ Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Central Angle“ (PDF) (англиски). Addison-Wesley. стр. 122. Посетено на 1 септември 2013.
↑ „Central angle (of a circle)“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен

Поврзани теми[уреди | уреди извор]

Надворешни врски[уреди | уреди извор]

Златковска, С. (2010). „Врска меѓу централен и периферен агол“. Архивирано од изворникот на 2018-07-25. Посетено на 1 декември 2013. интерактивен
„Central angle (of a circle)“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен
„Central Angle Theorem“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен

[Oxford-1] Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Central Angle“ (PDF) (англиски). Addison-Wesley. стр. 122. Посетено на 1 септември 2013.

[2] „Central angle (of a circle)“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен

[1]

[2]