Сплајн
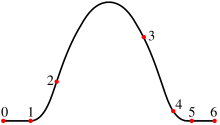
Сплајн (од анг. spline = „лајсна“) — посебна функција која се определува расцепкано со полиноми. При проблемите со интерполирање, честопати се претпочита сплајнова интерполација наместо полиномна бидејќи дава слични резултати (дури и кога користи полиноми од понизок степен), но ја одбегнува Рунгеовата појава кај вишите степени.
Кај сметачката графика, сплајновите се мошне застапени криви бидејќи се едноставни за конструирање, просто и точно се вреднуваат, и поради нивната способност да прават приближности на сложени облици прилагодување и интерактивна конструкција на криви.
Поимот „сплајн“ (spline) е преземен од еластичните свитливи лајсни што се користат во бродоградбата и проектирањето за исцртување на глатки криви облици.
Дефиниција[уреди | уреди извор]
Сплајнот е расцепкано-полиномна реална функција
на интервал [a,b] составен од k подредени разделени подинтервали со
- .
На секој интервал i, функцијата S е полином
- ,
така што
Редот на сплајнот (n) е еднаков на највисокиот ред на присутните полиноми , а полиномите треба да бидат такви што е непрекината и n-1 пати изведлива и во внатрешните јазолни точки . Ова значи дека во сите внатрешни јазолни точки за сите
Ако сите подинтервали се со иста должина, тогаш велиме дека сплајнот е рамномерен. Ако не се, тогаш сплајнот е нерамномерен.
Во голема мера најзастапени се кубните сплајнови, т.е. сплајновите од ред 3, бидејќи се користат за сплајнова интерполација која ја симулира функцијата на сплескани сплајнови.
Изведување на кубен сплајн[уреди | уреди извор]

Следниов извод прилагодува кубен сплајн на подредените парови со апциси и ординати , за . Ако земеме дека ни се познати вторите изводи во секоја точка , тогаш можеме да определиме параметризирана сплајнова функција со:[1]
каде A и B се определуваат:
- и
и
- и .
Можеме лесно да покажеме дека овој сплајн ги пресретнува сите подредени парови, а има втор извод
кој ги зачувува бараните изводи од втор ред во секоја позната точка.
За жал, изводите од втор ред не се познати и мора да ги пронајдеме. Ова можеме да го направиме со наложување на условот на непрекинатоста на првиот извод помеѓу интервалите. Ова значи дека изводот од кубниот сплајн
вреднуван со интервалот ( , ) мора да е еднаков на оној вреднуван со интервалот ( , ). Вака го добиваме следниов збир N-2 равенки со N непознати (вторите изводи):
- .
За да формулираме поблем што не е недоодреден, така што добиениот кубен сплајн ќе биде уникатен, ќе мора да назначиме уште два услова. „Природниот кубен сплајн“ користи услов на нулта закривеност во крајните точки на сплајнот, . Друга можност е да избереме први изводи во крајните точки и да ги замениве во првоизводната равенка за да ги исполниме преостанатите две равенки.
На крајот, изводот од кубниот сплајн се добива од решението на гореопишаните N равенки, и замената на второизведените решенија во сплајновата равенка, . Бидеќи секое решено закривување е поврзано (во однос) само со закривеноста на соседните делови, матрицата на решението на еден кубен сплајн секогаш ќе биде тридијагонална матрица и така може да се реши со O(N) операции со постоечки алгоритми на тридијагонална матрица.
Примери[уреди | уреди извор]

Еве прост пример за квадратен сплајн (од степен 2):
за кое .
Еве прост пример за кубен сплајн:
бидејќи
и
Еден пример кајшто применуваме сплајнови за составување на ѕвоновидната крива на веројатносната распределба се Ирвин-Холовите полиноми:
Историја[уреди | уреди извор]
Пред ерата на сметачите, пресметките се вршеле рачно и затоа се применува ле функции како скалестата функција. Со доаѓањето на сметачите, сплајновите ги замениле полиномите најпрвин во интерполацијата, а потоа почнале да се користат за конструирање на глатки и еластични облици кај сметачката графика.[2]
Сплајновите за прва пат се споменуваат во трудот на романскиот математичар Исак Јакоб Шенберг од 1946[3] што е веројатно првиот пример за употребата на „сплајн“ во смисла на глатка, расцепкана полиномна приближност. Меѓутоа овие идеи влечат корени во авиоконструкторството и бродоградбата.
Сплајнот како алатка (закривена лајсна) нашол примена во конструкцијата на авиони во Британија за време на Втората светска војна. Ваквото моделирање на крилата е позајмено од бродоградбата, кајшто овој облик се користел за исцртување на трупот на пловилото.
Во автоконструкторството, сплајнот се појавил независно на неколку места. Пионери во неговата употреба се Пол де Кастелжо од Citroën, Пјер Безје од Renault и Гарет Биркхоф, П.Р. Гарабедијан и Карл де Бор од General Motors.[4]
Поврзано[уреди | уреди извор]
Наводи[уреди | уреди извор]
- ↑ Press, W.H., Teukolsky, S.A., Vetterling, W.T., and Flannery, B.P., Numerical Recipes. The Art of Scientific Computing. III изд. Cambridge University Press. Cambridge, UK, 2007.
- ↑ Epperson, History of Splines, NA Digest, том 98, бр. 26, 1998.
- ↑ Schoenberg, Contributions to the problem of approximation of equidistant data by analytic functions, Quart. Appl. Math., том 4, стр. 45–99 и 112–141, 1946.
- ↑ Birkhoff, Fluid dynamics, reactor computations, and surface representation, in: Steve Nash (ed.), A History of Scientific Computation, 1990
- Stoer & Bulirsch, Introduction to Numerical Analysis. Springer-Verlag. стр. 93-106. ISBN 0387904204
- Chapra, Canale, "Numerical Methods for Engineers", V изд.
Надворешни врски[уреди | уреди извор]
| „Сплајн“ на Ризницата ? |
- Интерактивен вовед во сплајновите - ibiblio.org (англиски)
- Кориснички зададена функција на кубен сплајн за Excel (англиски)
- Алатка за интерполација на кубни сплајнови (англиски)
- Белешки, PPT, Mathcad, Maple, Mathematica, Matlab- Институт за холистички бројчени методи (англиски)

![{\displaystyle S:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/74953511637124762d95723d119b1d38fc8deaec)
![{\displaystyle [t_{i-1},t_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9be6f68e690582b18646e7c6afe955a30090915b)

![{\displaystyle P_{i}:[t_{i-1},t_{i}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c481a456bf3cd4fa71fd88bdb3102248f75a0c7)
































