Нидлман–Вуншов алгоритам

Класа	Порамнување на низи
Најлош случај
Просторна сложеност во најлош случај

Нидлман–Вуншовиот алгоритам е алгоритам кој се користи во биоинформатиката за порамнување на нуклеотидни или белковински низи. Овој алгоритам претставувал една од првите апликации на динамичкото програмирање за споредување на биолошките низи. Тој бил развиен од Саул Б. Нидлман и Кристијан Д. Вунш и објавен во 1970 година.^[1] Во суштина алгоритмот го дели поголемиот проблем (на пр. целосната низа) на серија помали проблеми, а потоа ги користи решенијата на помалите проблеми за реконструкција на решението на поголемиот проблем.^[2] Алгоритмот, исто така, е познат како алгоритам на оптимално совпаѓање, или како техника на глобално порамнување. Тој сѐ уште е широко применуван за оптимално глобално порамнување на низи, особено кога квалитетот на глобалното порамнување е од најголема важност.

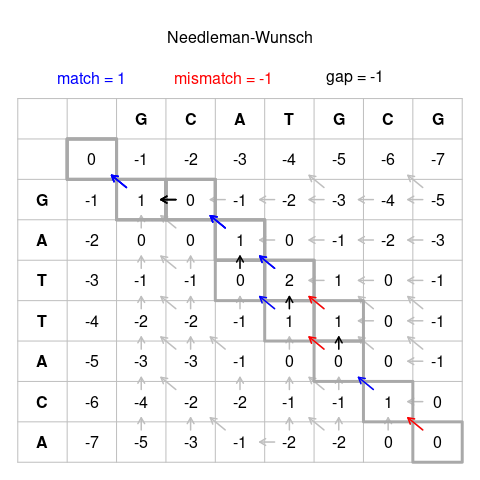
Слика 1: Нидлман-Вуншов алгоритам за порамнување во парови
Резултати: Низи Најдобри порамнувања --------- ---------------------- GCATGCU GCATG-CU GCA-TGCU GCAT-GCU GATTACA G-ATTACA G-ATTACA G-ATTACA Интерпретација на почетниот чекор: Левата колона во горната слика може да се толкува на следниот начин (ставајќи "+" пред секоја низа): Порамнување: +GCATGCU +GATTACA Бод: 0 // Се совпаѓаат, нема бод Порамнување: +GCATGCU +GATTACA Бод: 0 // 1 празнина, бод -1 Порамнување: +GCATGCU +GATTACA Бод: 0 // 2 празнини, бод -2 Порамнување: +GCATGCU +GATTACA Бод: 0 // 3 празнини, бод -3 Порамнување: +GCATGCU +GATTACA Бод: 0 // 4 празнини, бод -4 ... Истото може да се направи и за највисокиот ред.

Вовед[уреди | уреди извор]

Овој алгоритам може да се користи за кои било две низи. Следниот водич ќе користи две мали ДНК-низи како примери, прикажани во дијаграмот:

GCATGCU
GATTACA

Конструирање на координатна мрежа[уреди | уреди извор]

Прво се пристапува кон конструирање на координатна мрежа, како онаа прикажана на Слика 1 погоре. Започнете ја првата низа од врвот на третата колона, а втората низа од почетокот на третиот ред. Пополнете ги до крај, како што е прикажано на Слика 1. Сѐ уште не треба да има броеви во координатната мрежа.

		G	C	А	Т	G	C	U

G
А
Т
Т
А
C
А

Избор на систем за бодување[уреди | уреди извор]

Потоа, одлучете како ќе ги бодувате секој поединечен пар на букви. Употребувајќи го горниот пример, едно можно порамнување е:

12345678
GCATG-CU
G-ATTACA

Буквите (знаците) може да се совпаѓаат, да не се совпаѓаат, или да формираат празнина (бришењето или вметнување (индел)):

Совпаѓање: двете букви во тековниот индекс се исти.
Несовпаѓање: двете букви во тековниот индекс се различни.
Индел (ИНсерција или ДЕЛеција): во најдоброто порамнување има една буква која се порамнува со празнина во другата низа.

За секој од овие случаи се доделува одреден бод (бод) и збирот на бодовите за секој пар е бодот кој го добива целото кандидатно порамнување. Постојат повеќе различни системи за доделување на бодови; некои од нив се наведени подолу. Засега, ќе се употребува системот на Нидлман и Вунш:^[1]

Совпаѓање: +1
Несовпаѓање или Индел: -1

За примерот прикажан погоре, бодот на порамнувањето би бил 0:

GCATG-CU
G-ATTACA
+-++--+- -> -1*4 + 1*4 = 0

Пополнување на табелата[уреди | уреди извор]

Започнете со нула во вториот ред, втора колона. Движете се низ ќелиите ред по ред, пресметувајќи го бодот за секоја ќелија. Бодот се пресметува со споредување на бодовите на соседните ќелии на ќелијата во прашање: ќелијата од левата страна, горната ќелија и горната лева (дијагонална) ќелија, а потоа додавање на соодветниот бод за совпаѓање, несовпаѓање или индел. Потоа пресметајте ги кандидатните бодови на кандидатите за секоја од трите можности:

Патеката од горната или левата ќелија претставува спарување во индел, па затоа земете го бодот од левата и горната ќелија, и додадете го бодот за индел на секој од нив.
Дијагоналната патека претставува совпаѓање/несовпаѓање, па земете го бодот од горната лева дијагонална ќелија и додајте го бодот за совпаѓање, доколку соодветните бази во редот и колоната се совпаѓаат, или бодот за несовпаѓање, доколку соодветните бази во редот и колоната не се совпаѓаат.

Конечниот бод за ќелијата е највисокиот од трите кандидати.

Со оглед на тоа дека не постојат „погорни“ или „погорни леви“ ќелии за вториот ред, само постојната ќелија на лево може да се користи за пресметување на бодот на секоја ќелија. Па затоа се додава -1 за секое поместување надесно, што резултира со следните бодови за првиот ред: 0, -1, -2, -3, -4, -5, -6, -7. Истото важи и за втората колона, бидејќи може да се користи само постоечкиот бод над секоја ќелија. Така добиената табела е:

		G	C	А	Т	G	C	U
	0	-1	-2	-3	-4	-5	-6	-7
G	-1
А	-2
Т	-3
Т	-4
А	-5
C	-6
А	-7

Првиот случај, со постоечки бодови во сите 3 правци е пресекот на првите букви (во овој случај G и G). Дадени се околните ќелии:

		G
	0	-1
G	-1	X

Оваа ќелија има три можни вредности:

Дијагоналниот горно-лев сосед има бод 0. Парот на G и G е совпаѓање, па затоа додадете го бодот за совпаѓање: 0+1 = 1
Горниот сосед има бод -1, а движењето од таму претставува индел, па затоа додадете го бодот за индел: (-1) + (-1) = (-2)
Левиот сосед, исто така, има бод -1, претставува индел и, исто така, дава (-2).

Најголемиот кандидат е 1, и тој се внесува во ќелијата:

		G
	0	-1
G	-1	1

Ќелијата која го дава најголемиот кандидатен бод, исто така, мора да биде запаметена. Во комплетираниот дијаграм прикажан на слика 1 погоре, тоа е прикажано како стрелка од ќелијата во ред и колона број 3 кон ќелијата во ред и колона број 2.

Во следниот пример, дијагоналниот чекор за X и Y претставува несовпаѓање:

		G	C
	0	-1	-2
G	-1	1	X
А	-2	Y

Х:

Горе: (-2)+(-1) = (-3)
Лево: (+1)+(-1) = (0)
Горе-лево: (-1)+(-1) = (-2)

Y:

Горе: (1)+(-1) = (0)
Лево: (-2)+(-1) = (-3)
Горе-лево: (-1)+(-1) = (-2)

За X и Y, највисокиот бод е нула:

		G	C
	0	-1	-2
G	-1	1	0
А	-2	0

Најголемиот кандидатен бод може да се добие од две или од сите соседни ќелии:

	Т	G
Т	1	1
А	0	X

Горе: (1)+(-1) = (0)
Горе-лево: (1)+(-1) = (0)
Лево: (0)+(-1) = (-1)

Во овој случај, сите правци кои придонесуваат за највисокиот кандидатен бод мора да бидат обележани како можни ќелии на потекло во крајниот дијаграм на слика 1, на пр. во ќелијата во ред и колона 7.

Пополнувањето на табелата на овој начин ги дава бодовите за сите можни кандидати за порамнувањето, а бодот во ќелијата во долниот десен агол претставува бодот за најдоброто порамнување.

Следење на стрелките назад кон потеклото[уреди | уреди извор]

Обележете ја патеката од ќелијата во долниот десен агол назад кон ќелијата во горниот лев агол, следејќи ја насоката на стрелките. Од оваа патека, низата се конструирана врз основа на следните правила:

Дијагонална стрелка претставува совпаѓање или несовпаѓање, така што буквите од колоната и буквата од редот на ќелијата на потекло ќе бидат порамнети.
Хоризонтална или вертикална стрелка претставува индел. Хоризонталните стрелки ќе порамнат празнина („-“) со буквата од редот („страничната“ низа), вертикалните стрелки ќе порамнат празнина со буквата од колоната („горната“ низа).
Ако има повеќе стрелки од избор, тие претставуваат разгранување на порамнувањето. Ако две или повеќе гранки припаѓаат на патеки од долната лева ќелија до горната десна ќелија, тие се подеднакво добри порамнувања. Во овој случај, обележете ги патеките како посебни кандидати за порамнувањето.

Следејќи ги овие правила, чекорите за еден можен кандидат за порамнување од слика 1 се:

U → CU → GCU → -GCU → T-GCU → AT-GCU → CAT-GCU → GCAT-GCU
A → CA → ACA → TACA → TTACA → ATTACA → -ATTACA → G-ATTACA
          ↓
 (гранка) → TGCU → ...
          → TACA → ...

Системи за бодување[уреди | уреди извор]

Основни системи за бодување[уреди | уреди извор]

Наједноставните системи за бодување едноставно даваат вредност за секое совпаѓање, несовпаѓање и индел. Водичот опишан погоре користи вредности за совпаѓање = 1, несовпаѓање = -1, индел = -1. На овој начин, колку е понизок бодот на порамнувањето толку е поголемо Левенштајновото растојание, па така кај овој систем на бодување пожелен е повисок резултат. Друг систем на бодување може да биде:

Совпаѓање = 0
Индел = 1
Несовпаѓање = 1

За овој систем, бодот на порамнувањето ќе го претставува Левенштајновото растојание помеѓу двете низи. За различни ситуации можат да бидат создадени различни системи за бодување, на пример, ако празнините се сметаат за многу лоши за даденото порамнување, за нив можат да се дадат најголеми казнени бодови, како на пример:

Совпаѓање = 0
Несовпаѓање = 1
Индел = 10

Пробајте го овој пример.

Матрица на сличност[уреди | уреди извор]

Покомплицираните системи на бодување атрибутираат вредности не само за видот на промена, туку и за буквите кои се вклучени. На пример, совпаѓањето помеѓу A и A може да добие бод 1, но совпаѓањето помеѓу T и T може да добие бод 4. Овде, на пример, се дава поголемо значење на совпаѓањето на Т нуклеотидите отколку на A нуклеотидите, т.е. совпаѓањето на Т нуклеотидите се смета дека е поважно за порамнувањето. Ова мерење врз основа на букви исто така важи и за несовпаѓањата.

За да се претстават сите можни комбинации на букви и нивните резултирачки бодови, се користи матрица на сличност. Матрицата на сличност за најосновниот систем е претставена како:

	А	G	C	Т
А	1	-1	-1	-1
G	-1	1	-1	-1
C	-1	-1	1	-1
Т	-1	-1	-1	1

Секој бод претставува префрлање од една од буквите која ќелијата ја порамнува со другата. На тој начин, ова ги претставува сите можни совпаѓања и бришења (за азбука составена од буквите ACGT). Забележете дека сите совпаѓања се наоѓаат по должина на дијагоналата, а, исто така, дека не треба да биде пополнета целата табела, само еден триаголник, бидејќи резултатите се реципрочни. = (Бодот за A → C = Бодот за C → A). Ако го спроведувате правилото Т-Т = 4 од горе, се добива следната матрица на сличност:

	А	G	C	Т
А	1	-1	-1	-1
G	-1	1	-1	-1
C	-1	-1	1	-1
Т	-1	-1	-1	4

Статистички се конструирани различни матрици за бодување, кои даваат тежина на различни активности соодветни за одредено сценарио. Ова е особено важно кај порамнувањето на белковинските низи поради различната честота на различните аминокиселини. Постојат две поголеми семејства на матрици за бодување, од кои секоја претрпува дополнителни измени за прилагодување кон специфични сценарија:

PAM
BLOSUM

Казнени бодови за празнина[уреди | уреди извор]

При порамнувањето на низи, често се јавуваат празнини (т.е. индели), кои понекогаш можат да бидат доста големи. Од биолошка гледна точка, поголема е веројатноста да една поголема празнина се јави како резултат на една голема бришењето, а не како резултат на повеќе мали бришења. Затоа, два мали индела треба да имаат полош бод од еден голем индел. Наједноставниот и најчестиот начин да се направи ова е преку голем бод за нов индел и помал бод за продолжување на празнина за секоја буква која го продолжува инделот. На пример, нов индел може да чини -5 бода, а продолжување на индел може да чини -1 бод. На овој начин порамнувањето, како што е:

GAAAAAAT
G--A-A-T

кое има повеќе еднакви порамнувања, некои со повеќе помали порамнувања, сега ќе се порамни на следниот начин:

GAAAAAAT
GAA----Т

Напредно претставување на алгоритмот[уреди | уреди извор]

Бодовите за порамнетите карактери (знаци) се специфицирани со матрица на сличност. Овде, $S (a, b)$ е сличноста на знаците а и b. Таа користи линеарна казна за празнина, наречена $d$ .

На пример, ако матрицата на сличност е:

	А	G	C	Т
А	10	-1	-3	-4
G	-1	7	-5	-3
C	-3	-5	9	0
Т	-4	-3	0	8

тогаш порамнувањето:

AGACTAGTTAC
CGA---GACGT

со казна за празнина од -5 бода, ќе го има следниот збирен бод:

S (A,C) + S (G,G) + S (A,A) + (3 \times d) + S (G,G) + S (T,A) + S (T,C) + S (A,G) + S (C,T)

= -3 + 7 + 10 - (3 × 5) + 7 + (-4) + 0 + (-1) + 0 = 1

За да се најде порамнувањето со највисок бод, се распределува дво-димензионална низа (или матрица) F. Записот во ред i и колона j е означен со $F_{ij}$ . Постои еден ред за секој карактер на низата A, и една колона за секој карактер на низата B. На овој начин, ако се порамнуваат низи со големини n и m, количината на меморија која се користи е во $O(nm)$ . Хиршберговиот алгоритам содржи само подмножество на низата во меморија и користи $\Theta (\min\{n,m\})$ простор, а во секој друг поглед е сличен на Нидлман-Вуншовиот алгоритам (и исто така бара $O(nm)$ време).

Како што алгоритмот напредува, $F_{ij}$ ќе биде назначен да биде оптималниот бод за порамнувањето на првите $i=0,\dotsc ,n$ карактери во A и првите $j=0,\dotsc ,m$ карактери во B. Потоа се применува принципот на оптималност на следниов начин:

Основа:

F_{0j}=d*j

F_{i0}=d*i

Рекурзија, врз основа на принципот на оптималност:

F_{ij}=\max(F_{i-1,j-1}+S(A_{i},B_{j}),\;F_{i,j-1}+d,\;F_{i-1,j}+d)

Псевдо-кодот за алгоритмот за пресметување на F матрицата изгледа вака:

d ← бод за несовпаѓање
за i=0 до должина(A)
  F(i,0) ← d*i
за j=0 до должина(B)
  F(0,j) ← d*j
за i=1 до должина(A)
  за j=1 до должина(B)
  {
    Match ← F(i-1,j-1) + S(A_i, B_j)
    Delete ← F(i-1, j) + d
    Insert ← F(i, j-1) + d
    F(i,j) ← max(Match, Insert, Delete)
  }

Откако ќе се пресмета F матрицата, записот $F_{nm}$ го дава максималниот бод меѓу сите можни порамнувања. За да се пресмета порамнувањето кое, всушност, го дава овој бод, се започнува од долната десна ќелија, и се споредува вредноста со трите можни извори (Match, Insert, Delete, наведени погоре) за да се утврди од кого потекнува. Ако е Match, тогаш $A_{i}$ и $B_{j}$ се порамнуваат, ако е Delete, тогаш $A_{i}$ е порамнета со празнина, и ако е Insert, тогаш $B_{j}$ е порамнета со празнина. (Во принцип, истата вредност може да ја имаат повеќе порамнувања, што доведува до алтернативни оптимални порамнувања.)

ПорамнувањеA ← ""
ПорамнувањеB ← ""
i ← должина(A)
j ← должина(B)
додека (i > 0 или j > 0)
{
  ако (i > 0 и j > 0 и F(i,j) == F(i-1,j-1) + S(A_i, B_j))
  {
    ПорамнувањеA ← A_i + ПорамнувањеA
    ПорамнувањеB ← B_j + ПорамнувањеB
    i ← i - 1
    j ← j - 1
  }
  или ако (i > 0 и F(i,j) == F(i-1,j) + d)
  {
    ПорамнувањеA ← A_i + ПорамнувањеA
    ПорамнувањеB ← "-" + ПорамнувањеB
    i ← i - 1
  }
  или
  {
    ПорамнувањеA ← "-" + ПорамнувањеA
    ПорамнувањеB ← B_j + ПорамнувањеB
    j ← j - 1
  }
}

Комплексност[уреди | уреди извор]

Пресметувањето на бодот $F_{ij}$ за секоја ќелија во табелата е $O(1)$ операција, па затоа на временската комплексност на алгоритмот за две низи со должина $n$ и $m$ е $O(mn)$ .^[3] Било покажано дека е можно да се подобри времето на извршување на $O(mn/\log n)$ со употреба на т.н. Метод на Четирите Руси.^[3]^[4] Бидејќи алгоритмот пополнува $n\times m$ табела, просторната комплексност е $O(mn)$ .^[3]

Поврзано[уреди | уреди извор]

Наводи[уреди | уреди извор]

↑ ^1,0 ^1,1 Needleman, Saul B. & Wunsch, Christian D. (1970). „A general method applicable to the search for similarities in the amino acid sequence of two proteins“. Journal of Molecular Biology. 48 (3): 443–53. doi:10.1016/0022-2836(70)90057-4. PMID 5420325.
↑ „bioinformatics“. Посетено на 10 September 2014.
↑ ^3,0 ^3,1 ^3,2 Wing-Kin., Sung (2010). Algorithms in bioinformatics : a practical introduction. Boca Raton: Chapman & Hall/CRC Press. стр. 34–35. ISBN 9781420070330. OCLC 429634761.
↑ Masek, William; Paterson, Michael (February 1980). „A faster algorithm computing string edit distances“. Journal of Computer and System Sciences. 20: 18–31. doi:10.1016/0022-0000(80)90002-1 – преку Elsevier Science Direct.

Надворешни врски[уреди | уреди извор]

[Needleman-1] 1,0 ^1,1 Needleman, Saul B. & Wunsch, Christian D. (1970). „A general method applicable to the search for similarities in the amino acid sequence of two proteins“. Journal of Molecular Biology. 48 (3): 443–53. doi:10.1016/0022-2836(70)90057-4. PMID 5420325.

[2] „bioinformatics“. Посетено на 10 September 2014.

[:0-3] 3,0 ^3,1 ^3,2 Wing-Kin., Sung (2010). Algorithms in bioinformatics : a practical introduction. Boca Raton: Chapman & Hall/CRC Press. стр. 34–35. ISBN 9781420070330. OCLC 429634761.

[4] Masek, William; Paterson, Michael (February 1980). „A faster algorithm computing string edit distances“. Journal of Computer and System Sciences. 20: 18–31. doi:10.1016/0022-0000(80)90002-1 – преку Elsevier Science Direct.

[1]

[2]

[3]

[4]