Диелектрик
Диелектрик е електричен изолатор кој може да биде поларизиран со примена на електрично поле. Кога диелектрикот е ставен во електричното поле, електричните полнежи не течат низ материјалот како кај проводниците, но само малку се поместуваат од нивната рамнотежна позиција предизвикувајки диелектрична поларизација. Поради оваа поларизација, позитивните полнежи се поместуваат во насока на полето, а негативните во спротивната насока. Ова придонесува за создавање на внатрешно електрично поле кое делумно го надоместува надворешното поле во внатрешноста на диелектрик. Ако диелектрикот е составен од слабо врзани молекули, молекулите не само што стануваат поларизирани туку и се преорентираат така што нивната оска на симетрија се поклопува со насоката на надворешното поле. Иако поимот изолатор се однесува на низок степен на електрична спроводливост, терминот диелектрик обично се користи за да опише материјали со висок поларизација. Поларизацијата се изразува со број кој е наречен диелектрична константа. Често сретнуван, но сепак значаен пример на диелектрик е електрично изолациониот материјал помеѓу металните плочи на кондензаторот. Поларизацијата на диелектрик од страна на електричното поле го зголемува полнежот на плочите на кондензаторот. Истражувањето на диелектричните својства се занимава со складирањето и дисипацијата на електричната и магнетната енергија во материјалите. Тоа е од голема важност за да се објаснат разни феномени во електрониката, оптиката и физиката на тврдите материи.
Поимот диелектрик прв го употребил Вилијам Вевел како одговор на барање на Мајкл Фарадеј.
Електрична суксептибилност[уреди | уреди извор]
Електрична суксептибилност χe на диелектричен материјал е мерка за тоа колку лесно материјалот се поларизира како одговор на електричното поле. Ова пак ја одредува диелектричната константа на материјалот која влијае на многу други појави во тој медиум, капацитетот на кондензатори до брзината на светлината. Таа е дефинитана како константа на пропорционалност (која може да биде тензор) која го поврзува електричното поле Е со густината на индуцираната поларизација P,
Каде што е електричен пермеабилитет на слободен простор. Суксептибилност на медиумот е поврзан со неговиот релативен пермеабилитет со
Значи во вакуум, Електричното поместување D е поврзано со густината на поларизација Р;
Расејување[уреди | уреди извор]
Во принцип, материјалот не може веднаш да се поларизира како одговор на даденото поле. Погенерална формула како функција од времето, е дадена со
Значи, поларизацијата е спираловидност на електричното поле во претходните времиња со временски зависна susceptibility . Горниот лимит на овој интеграл може да се продолжи до бесконечност ако се дефинира за . Инстантен одговор на материјалот кога е ставен во електрично поле се одликува со Дирак делта функција од susceptibility . Во линеарен систем, попогодно е да се земе Фириерова трансформација и ова да се запише како функција од честотата. Поради спираловиднос теорема, интегралот станува едноставен производ, Susceptibility исто како и диелектричната константа имаат едноставна зависност од честотата. Обликот на граф на susceptibility во однос на честотата ги карактеризира расејувачките својства на материјалот. Исто така, фактот дека поларизацијата може да зависи само од електричното поле во претходните времиња, времиња (i.e. for ), како последица од causality, наметнува Крамерс-Крониг ограничувања на susceptibility .
Диелектрична поларизација[уреди | уреди извор]
Основен атомски модел[уреди | уреди извор]
Во класичниот пристап кон модел за диелектрик, материјата се состои од атоми. Секој атом се состои од облак на негативен полнеж (електрони) кои се врзани за и обиколуваат околу позитивен полнеж во неговиот центар. Пордаи релативното голема дистанца мегу нив, ниту еден од атомите во диелектричните материјали немаат интеракција еден со друг. (Овој модел не се обидува да ја опише структурата на материјата, туку на интеракцијата помеѓу електричното поле и материјата). Во присуство на електрично поле негативниот облак е искривен како што е прикажано во горниот десен агол на сликата. Ова може да се сведе на едноставен дипол користејки го принципот на суперпозиција. Диполот се одликува со свој диполен момент, вектор прикажан на сликата како сина стрелка со ознака М. Односот помеѓу електричното поле и диполниот момент резултира во прикажаното однесување на диелектрик. (Забележете дека диполниот момент е прикажан посочувајки во иста насока како и електричното поле. Ова не е секогаш точно и е големо поедноставување, но тоа е погодно за многу материјали). Кога електричното поле ќе се отстрани атомот се враќа во првобитната состојба. Времето потребно да го стори тоа се нарекува време на релаксација: кое има експоненцијална форма. Ова е суштината на моделот во физиката. Понатаму однесувањето на диелектрикот зависи од ситуацијата. Колку што се усложнува ситуацијата, толку побогат модел е потребен, со цел прецизно да го опише однесувањето. Важни прашања се:
- Дали електричното поле е константно или варира со времето?
- Ако електричното поле варира, со која брзина варира?
- Кои се одликите на материјалот?
- Дали е важна насоката на полето ?
- Дали материјалот е хомоген?
- Дали постојат граници кои треба да бидат земени предвид?
- Дали системот е линеарен или има нелинеарности кои треба да бидат земени предвид?
Односот помеѓу електричното поле Е и диполниот моемент М доведува до однесувањето на диелектрикот, кој, за одреден материјал може да се одликува со функцијата F, дефинирана од страна на равенката
- .
Кога и типот на електричното поле и видот на материјалот се дефинирани, треба да се избере наједноставната функција F која точно ги предвидува феномените кои не интересираат. Примери на феномени кои можат да бидат проучувани се: • Показател на прекршување • Расеаност на групна брзина • Бирефригенција • Самососредоточување • Хармонична генерација
Диполна поларизација[уреди | уреди извор]
Диполната поларизација е поларизација која е најзастапена кај поларните молекули. Оваа поларизација е резултат на постојани диполи, на пример асиметричните врски помеѓу кислородни и водородни атоми кои имаат поларизација и без присуство на надворешно електрично поле. Собирањето на сите диполи ја формира макроскопската поларизација Кога ќе се примени надворешно електрично поле, растојанието помеѓу полнежите, кое е поврзано со хемиското сврзување, останува константно во поларизацијата, мегутоа поларизацијата ротира. Оваа ротација се појавува на временска рамка која зависи од вртежниот момент и вискозноста на околните молекули. Бидејќи ротацијата не е моментална, биполните поларизации го губат одговорот на електричните полиња со најниска честота. Одложувањето на одговорот на промената на електричното поле предизвикува триење и топлина.
Јонска поларизација[уреди | уреди извор]
Јонска поларизација е поларизација која е предизвикана од мегусебната оддалеченост мегу позитивните и негативните јони во јонски кристали (NaCl). Ако кристалите или молекулите не се состојат само од атоми од ист вид, дистрибуцијата на полнеж околу еден атом во кристалот или молекулата има тенденција да биде позитивна или негативна. Како резултат на ова, кога вибрации во кристалната решетка или молекуларните вибрации ќе предизвикаат одделување на атомите, центрите на позитивните или негативните полнежи можат да бидат на различни локации. Овие локации се погодени од симетријата на преместувањата. Кога центрите не се поклопуваат, во молекулите или кристалите се појавува поларизација. Оваа поларизација се вика јонска поларизација. Јонската поларизација предизвикува феро електрична транзиција исто како и диполна поларизација. Транзицијата која е предизвикана од ориентацијата на постојаните диполи во одредена насока се нарекува order disorder phase transition. Транзицијата која е предизвикана од јонската поларизација во кристали се нарекува displacive phase transition.
Диелектрично расејување[уреди | уреди извор]
Во физиката, диелектричното расејување е зависноста на диелектричната константа од честотата на надворешното електрично поле. Бидејќи секогаш постои застој помеѓу промените во поларизацијата и промените во електричното поле, диелектричната константа е комплицирана, имагинарна функција од честотата на електричното поле. Тоа е многу битно за апликацијата на диелектричните материјали и анализа на системите на поларизација. Ова е еден случај од општ феномен познат како материјално расејување: одговор на медиум на ширење на бранот кој е зависен од честотата. Кога честотата станува повисока: 1. Диполната поларизација не може да ги следи промените во електричното поле во микробрановиот регион, околу 1010 Hz 2. Во инфрацрвениот или далеку инфрацрвениот регион околу 1013 Hz јонската поларизација го губи одговорот на електричното поле 3. Електронската поларизација го губи својот одговор во ултравиолетовата област околу 1015 Hz. Во регионот под ултравиолетовата бранова должина, диелектричната константа се доближува до ε 0 во секоја супстанција, каде ε 0 е пермеабилитет на слободен простор. Бидејќи пермеабилитет ја покажува силата на односот помеѓу електричното поле и поларизацијата, ако поларизацијата го губи својот одговор, диелектричната константа се намалува.
Диелектрична релаксација[уреди | уреди извор]
Диелектрична релаксација е моментно одложување(или застој) во диелектричката константа на материјалот. Ове е обично предизвикано од доцнењето на молекуларната поларизација во однос на менувањето на електричното поле во диелектричен медиум. (на пример помеѓу кондензатори или помеѓу две многу големи спроводливи површини). Диелектричката релаксација во менувањето на електричното поле може да се смета за аналог на хистерезис во менувањето на магнетното поле (за намотки или трансформатори). Релаксацијата најчесто е одложување или застој во одговорот на линеарен систем, и затоа диелектричната релаксација се мери во однос на очекуваните линеарни стабилни состојби (рамнотежа) на диелектричните вредности. Заостанувањето на времето помеѓу електричното поле и поларизацијата подразбира неповратна деградација на енергијата(G). Во физиката, диелектрична релаксација се однесува на одговорот на диелектричен медиум на надворешно електрично поле во областа на микробранови честоти. Оваа релаксација често се објаснува користејки ја диелектричната константа како функција од честотата, што за идеални системи е опишана со Дебуевата равенка. Од друга страна, искривувањето поврано со јонска и електронска поларизација покажува однесување на резонанца од осцилаторен тип. Карактерот на искривувањето зависи од структурата, составот и околината на примерокот. Бројот на можни бранови должини на зрачење поради релаксацијата на диелектрикот можат да се пресметаат со првиот Хемингсов закон (наречен по Марк Хемингс),
каде што n е број на различни бранови должини на емитирано зрачење l е бројот на енергетско ниво (вклучувајќи основно ниво).
Дебуе релаксација[уреди | уреди извор]
Дебуе релаксација е диелектрична релаксација на идеална популација на диполи кои не реагираат мегу себе, како одговор на надворешно електрично поле. Таа обично се мери во имагинарен пермеабилитет на медиум како функција од честотата на надворешното поле ,
каде што е пермеабилитет на лимитот на висока честота , where каде што е статичен, пермеабилитет на ниска честота и е карактеристично време на релаксација на медиумот. Овој модел на релаксација бил претставен од страна и го носи името на хемичарот Петар Дебуе (1913).
Варијанти на Дебуевата равенка[уреди | уреди извор]
- 1.Кол-кол равенка
- 2.Кол-Дејвидсон равенка
- 3.Хаврилак-Негами релаксација
- 4.Колрауч-Вилијамс-Вотс функција (Фуриеова трансформација на протегната експоненцијална функција)
Апликации[уреди | уреди извор]
Кондензатори[уреди | уреди извор]
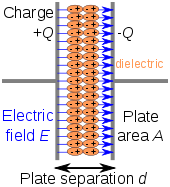
Комерцијално произведените кондензатори обично користат цврст диелектричен материјал со висока диелектрична константа како медиум кој ги разделува позитивните и негативните полнежи. Овој материјал често е нарекуван во технички контекст како кондензаторен диелектрик. Најочигледна предност на користењето на ваков материјал е што тој го спречува директниот електричен контакт на двете проводни плочи на кои се складирани полнежите. Сепак, позначајно е тоа што висок пермеабилитет овозможува на даден напон да се складира поголемо количество на полнежи. Ова може да се види преку третирање на случајот на линеарен диелектрик со диелектрична константа ε и дебелина d меѓу двете плочи на кои е складирана униформна густина на полнеж σ ε. . Во овој случај густината на полнеж е дадена со равенката,
и капацитет на единица површина од
Од ова, таа лесно може да се види дека поголемо ε води кон поголема акумулација на полнежи и со тоа поголем капацитет. Диелектричните материјали кои се користат во кондензатори исто така се избрани за да бидат отпорни на јонизација. Ова им овозможува на кондензаторите да работат на висок напон пред диелектрикот да се јонизира и да почне да спроведува несакани струи.
Диелектричен резонатор[уреди | уреди извор]
Диелектричен резонатен осцилатор (DRO) е електронски компонент кој покажува резонанца во релативно тесен спектар на честоти, генерално во микробрановиот простор. Тој се состои од puck од керамика кој има голема диелектрична константа и низок фактор на дисипација. Таквите резонатори се најчесто употребувани за да се обезбеди референтна честота во оцилаторно коло. Непокриен диелектричен резонатор може да се користи како Диелектрична резонаторна Антена (DRA).
Некои практични диелектрици[уреди | уреди извор]
Диелектричните материјали можат да бидат цврсти материи, течности или гасови. Покрај тоа, голем вакуум исто така може да биде корисен диелектрик иако неговата релативна диелектрична константа е 1. Цврстите диелектрици се можеби најчесто користени диелектрици во електротехниката, а многу цврсти тела се добри изолатори. Некои примери вклучуваат порцелан, стакло, и највеќе пластика. Воздух, азот и сулфур хексафлорид се трите најчесто користени гасни диелектрици. • Индустриски премази како parylene обезбедуваат диелектрична бариера помеѓу подлогата и неговата околина. • Минералното масло се користи во голема мера во електричните трансформатори како течен диелектрик и да асистира во ладењето. Диелектричните течности го повисоки диелектрични константи како што е electrical grade castor oil најчесто се користат во кондензатори кои работат на висок напон за да спречат corona discharge и да се зголеми капацитетот. • Бидејќи диелектриците се противат на протокот на електрична енергија, површината на диелектрикот може да го задржи вишокот на полнежи. Ова може да се случи случајно, кога диелектрикот е протриен (triboelectric effect). Ова може да биде корисн, како на Ван де Грааф генератор или би можело да биде потенцијално деструктивно како што е во случај на електричните празнења. • Специјално преработените диелектрици, наречени електрети (ferroelectrics) можат да задржат вишок на внатрешни полнежи или замрзната поларизација. Електретите имаат полу постојано надворешно електрично поле и тие се електростатички аналог на магнет. Електретите имаат многу апликации низ домовите и во индустријата. • Некои диелектрици можат да генерираат потенцијална разлика кога се подложени на механички стрес или можат да ја променат физичката форма ако се подложени на надворешен напон. Ова својство е наречено пизоелектричество. Пизоелектричните материјали се друга класа на многу корисни диелектрици. • Некои јонски кристали и полимерски диелектрици покажуваат спонтан диполен момент кој може да биде променет со применување на електрично поле однадвор. Ова се нарекува ferroelectric ефект. Овој начин е аналог на начинот на кој феро магнетите реагираат со магнетно поле применето однадвор. Фероелектричните материјали имаат многу високи диелектрични константи, што ги прави многу корисни за употреба за кондензатори.
Наводи[уреди | уреди извор]
- Давид Џексон: Класична Електродинамика. Вили, Њујорк 1998
|
























