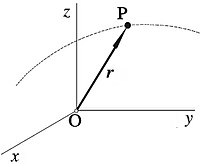
Радиус-вектор

Радиус-вектор на една честица во Декартовиот координатен систем.

Радиус-векторот или вектор на положбата (најчесто се означува $\vec r$ или $\mathbf r$) е вектор кој ја опишува положбата на една точка во просторот во однос на некоја друга фиксна точка (која е референтно тело) наречена координатен почеток, која го претставува векторскиот почеток, а крајот на векторот е во точката чија положба ја одредува. Во тридимензионалниот Декартов координатен систем, радиус-векторот се определува од равенката:

$\mathbf r = x\mathbf i + y\mathbf j + z\mathbf k$

каде x, y, z се координати (апсциса, ордината и апликата) на точката, а $\mathbf i$, $\mathbf j$ и $\mathbf k$ се единични вектори на соодветните координати.

Доколку дадена точка се движи, односно ја менува својата положба во текот на времето, тогаш радиус-векторот со својот врв ја опишува траекторијата на точката. Математички изразена, промената на положбата на векторот во зависност од времето се нарекува параметарска равенка на траекторијата:

$\mathbf{r} = \mathbf{r}(t) \,,$

каде со t е означено времето, која всушност претставува параметарски зададена равенка на крива која точката ја испишува во текот на своето движење.

Векторот на поместување d на една точка за одреден временски интервал $t = [t_1, t_2]$ може да се добие со векторско одземање на почетниот од крајниот радиус-вектор:

$\mathbf{d} = \mathbf{r}(t_2) - \mathbf{r}(t_1) \,,$

каде $t_1$ означува почетен, а $t_2$ краен момент на времето.