Тесеракт
| Тесеракт 16-ќелијник (16-коцка) | |
|---|---|
 | |
| Вид | испакнат правилен многуќелијник |
| Шлефлиев симбол | {4,3,3} t0,3{4,3,2} или {4,3}×{ } t0,2{4,2,4} или {4}×{4} t0,2,3{4,2,2} или {4}×{ }×{ } t0,1,2,3{2,2,2} или { }×{ }×{ }×{ } |
| Коксетеров дијаграм | |
| Ќелии | 8 {4,3} |
| Страни | 24 {4} |
| Рабови | 32 |
| Темиња | 16 |
| Темена фигура |  тетраедар |
| Петриев многуаголник | осумаголник |
| Коксетерова група | B4, [3,3,4] |
| Двојствено | 16-ќелијник |
| Својства | испакнат, изоголален, изотоксален, изоедарски |
| Рамномерен показател | 10 |
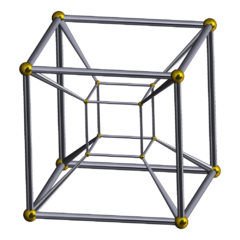
Тесеракт (четиридимензионална хиперкоцка) — четиридимензионалнен аналог на коцката. Тоа значи дека, тесерактот е за коцката она што коцката е за квадратот. Поформално, тесерактот е правилен испакнат многуќелијник со осум коцкести ќелии. Зборот тесеракт се мисли дека е измислен од Чарлс Хавард Хинтон.
Воопштувањата на коцката со повеќе од три димензии се нарекуваат хиперкоцки или мерни политопи. Ова статија зборува за 4Д-хиперкоцката наречена „тесеракт“.
Геометрија[уреди | уреди извор]
Стандардниот тесеракт во Евклидовиот 4-простор е даден како испакната обвивка на точките (±1, ±1, ±1, ±1). Тоа значи дека тесератктот се состои од точките:
Тесерактот е ограничен со осум хиперрамнини (xi = ±1). Секој пар од непаралелни хиперрамнини се вкрстува и сочинува 24 квадратни страни на тесерактот. Три коцки и три квадрати се сечат при секој раб. Четири коцки, шест квадрати и четири раба се сретнуваат во секое теме. Сѐ на сѐ, тесерактот се содржи од 8 коцки, 24 квадрата, 32 раба, и 16 темиња.
Бидејќи секое теме на еден тесеракт е напореден на четири раба, теменото тело на тесерактот е правилен тетраедар. Затоа тесерактот носи Шлефлиева ознака {4,3,3}. Дуалниот политоп на тесерактот се нарекува хексадекаедар или 16-ќелијник, со Шлефлевиева ознака {3,3,4}.
Проекции на 2 димензии[уреди | уреди извор]
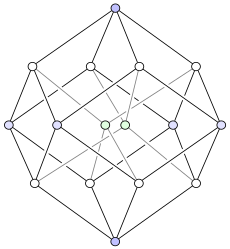
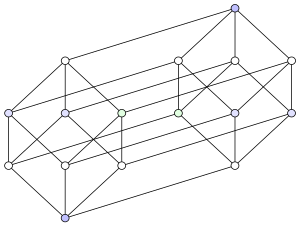
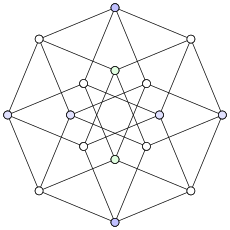
Овој објект не е лесно замислив, но можно е да се проектираат тесеракти на три и дводимензионални простори. Освен тоа, проекциите на 2Д-рамнина се уште покорисни со преместување на местата на проектираните темиња. На овој начин, можеме да добиеме слики кои повеќе не го одразуваат просторниот сооднос во рамките на тесерактот, но кои ја илустрираат структурата на поврзаност на темињата. Еве примери:
 |
 |
|
Првата илустрација покажува како во принцип се добива тексеракт со комбинација на две коцки. Шемата е слична на правењето на коцка од два квадрата: ставите два примерока од подолнодимензионалната коцка едне на друг и спојте ги соодветните темиња. Втората слика го образложува фактот што секој раб на тесерактот е со иста должина. Оваа слика ито така му овозможува на човечкиот ум да најде мноштво коцки кои се фино меѓусебно поврзани. Третиот дијаграм конечно ги поредува темињата на тесерактот во оглед на раздалеченоста низ рабовите, во оглед на најдолната точка.
Проекции на 3 димензии[уреди | уреди извор]
Првоќелинјата паралелна проекција на тесерактот во тридимензионален простор има коцкеста обвивка. Најблиските и најдалеките ќелии се проектирани на коцката, а оистанатите 6 ќелии се проектирани на 6-те квадратни страни на коцката.
Првостраничната паралелна проекција на тесерактот во тридимензионален простор има кубоидна обвивка. Два дела од една ќелија се прокетираат на горната и долната површина на обвивката, а 4-те станати ќелии се проектираат на страничните лица.
Прворабната паралелна проекција на тесерактот во тридимензионалниот простор има обвивка во облик на шестаголна призма. 8-те ќелии се проектираат на волуменот на призмата во облик на паралелограмски призми, кои се поставени на шестаголната призма на начин кој е аналоген на тоа како лицата на 3Д коцката се проектираат врз 6 паралелограми во честоаголна обвивка под првотемената проекција.
Првотемената паралелна проекција на тесерактот во тридимензионален простор има ромбско додекаедарска обвивка. Постојат токму два начина на разложување на ромбски додекаедар на 4 ускладени паралелопипеди, давајќи заедно 8 можни паралелопипеди. Сликите на ќелиите на тесерактот под оваа проекција се токму овие 8 паралелопипеди. Ова проекција е проекцијата со максимален волумен.
На некој начин, во четиридимензионален свет со „ветер“, мрежата на тесерактот би била екстремно нестабилна и би била соборена, „смачкувајќи“ ја „страната на коцката“ врз кој би паднала. Ова е слично на тоа како дводимензионална мрежа на коцка би била нестабилна со ветер, паѓајќи врз една од нејзините две страни.
Разложување[уреди | уреди извор]
Тесерактот може да се разложи на осум коцки, како што коцката се разложува на шест квадрати (анимација). Ова разложување се нарекува мрежа Тесерактот има 261 засебни мрежи.[1] Разложените елементи можат да се избројат со пресликување на спарени стебла (стебло со спарено во неговиот комплемент).
Поврзано[уреди | уреди извор]
- Хипертопка (хиперсфера)
- Хиперрамнина
- Накрсен политоп
- Симплекс
- Многуќелијник
- Список на правилни политопи
- Четврта димензија
Наводи[уреди | уреди извор]
- ↑ „Разложување на 8-ќелијник“. (англиски)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

