Неопределени контролни системи
Неопределени контролен систем е контролен систем заснован на неопределена логика, односно математички систем кој анализира аналогни влезови кои примаат континуални вредности помеѓу 0 и 1, за разлика од класичната или дигитална логика каде влезовите се дискретни, односно 1 или 0 (вистина или невистина соодветно).
Фази контролен систем е контролен систем заснован на непрецизна логика, односно математички систем кој анализира аналогни влезови кои примаат континуални вредности помеѓу 0 и 1, за разлика од класичната или дигитална логика каде влезовите се дискретни, односно 1 или 0(вистина или невистина соодветно).
Преглед[уреди | уреди извор]
Непрецизната логика има широка употреба во машинската контрола. Терминот непрецизна самиот по себе воведува доза на скептицизам, звучи како нецелосна логика или како лажна логика. Но делот непрецизна не се однесува на недостаток или ограниченост на методот, туку на фактот дека непрецизната логика може да се справи со непрецизни концепти-концепти што не можат да се изразат со вистина или невистина, туку со делумна вистина. Исто така и генетските алгоритми и невронските мрежи можат да дадат добри резултати исто како и непрецизната логика, но предноста на непрецизната логика се состои во тоа што таа дава резултати коишто можат да бидат разберени од човекот, па така ова искуство може да се искоисти за во дизајн на контролерот. Со ова се олеснува механизирањето на задачите кои претходно биле успешно спроведувани од луѓето.
Непрецизно множество[уреди | уреди извор]
Влезните променливи на фази контролниот систем се мапирани во множества на припадност кои се определуваат според некоја функција на припадност, познати како непрецизни множества. Процесот на претворање на “крисп” вредноста на влезот во фази вредност се нарекува “фазификација”. Врз основа на дадените мапирања на влезните променливи во функции на припадност и вистински вредности, микроконтролерот одлучува каква акција да преземе врз основа на множество на правила, претстванеи во следниот облик:
АКО вредноста на температурата Е топло И брзината Е не многу брзо ТОГАШ притисокот Е благо намален.
Во овој пример, двете влезни променливи се “температура” и “брзина”. Овие променливи имаат вредности дефинирани како непрецизни множества. Излезната променлива “притисок”, е исто така дефинирана како непрецизно множество кое може да има вредности како “константен”, “благо покачен”, “благо намален”, итн. На прв поглед може да се каже дека ова правило може да се користи без да се употреби непрецизна логика, но кога одлуката седонесува врз основа на повеќе правила тогаш:
- Сите правила што се применуваат се вклучени, користејќи ги функциите на припадност и вистинските вредности добиени на влез, за да се одредат резултатите на правилото.
- Овој резултат ќе биде мапиран во функција на припадност и вистинска вредност која ќе ја контролира излезната променлива.
- Овие резултати се комбинираат за да се добие соодветната крисп вредност како одговор, моменталниот brake pressure, процедура позната како дефазификација.
Оваа комбинација на непрецизни операции и заклучување засновано на правила го опишуваат непрецизниот експертен систем. Традиционалните контролни системи се засноваат на математички модели во кои контролата на системот е опишана со користење на една или повеќе различни равенки кои го дефинираат излезот кој ќе го даде системот според влезовите кои ги добива. таквите системи најчесто се имплементираат како "PID контролери" (пропорционално-интегрирани-изведени контролери). Тие се резултат на долгогодишен развој и теоретски анализи, и се високо ефективни. Ако PID и другите традиционални контролни системи се толку добро развиени тогаш зошто да се занимаваме со непрецизна логика? Таа има неколку предности. Во повеќето случаи математичкиот модел кој би бил решение на контролниот процес може да не постои, или да биде премногу скап во однос на обработувачката моќ и меморија, и системот заснован на емпириски правила може да биде поефективен. Според тоа, непрецизната логика е соодветна за имплементација на поевтини имплментации засновани на евтини сензори, аналогно-дигитални претворачи со слаба резолуција итн. Ваквите системи ќе можат лесно да бидат надоградувани со додавање на нови правила за да се подобрат перформансите или да се додават нови одлики. во повеќето случаи, непрецизната логика може да се користи за да се подобрат веќе постоечките традиционални системи за контрола со додавање на дополнителен слој на интелигенција на моменталниот контролен метод.
Непрецизна контрола во детали[уреди | уреди извор]
Непрецизните контролери концептуално се многу едноставни. Тие се состојат од влезна етапа, обработувачка и излезна етапа. Влезната етапа го мапира излезот од сензорот, или други излези, на пример од прекинувачи и слично во соодветната функција на припадност и вистинита вредност. Обработувачката етапа ги повикува соодветните правила и генерира резултат за секој, потоа ги комбинира резултатите од правилата. И на крај излезната етапа ги претвора комбинираните резултати назад во специфична излезна вредност.
Најчесто користена функција на припадност е триаголната функција, потоа трапезоидната итн, но формата на кривата и не е толку важна, колку што е важно колку криви има и каде се поставени. Обично се ористат од 3 до 7 криви за да го покријат опсегот на влезната вредност. Како што е спомнато претходно, обработувачката етапа се заснова на колекција на логички правила кои се во облик АКО-ТОГАШ, каде делот се нарекува причина, додека ТОГАШ делот се нарекува поседица. Типичен фази систем има десетина правила. Следново правило е правило за термостат:
АКО (температура е “студена”) ТОГАШ (загревањето е “високо”)
Ова правило ја користи вистинската вредност на влезот “температура”, која има вредност “студено”, за да генерира резултат во непрецизнот множество за излезот “загревање”, кој има вредност “високо”. Овој резултат се користи заедно со резултатите на другите правила за конечно да се генерира крисп вредноста како излез. Очигледно колку е поточна вредноста за “студено”, толку е поточна вредноста “високо”, иако ова не мора да значи дека излезот ќе се добие вредност “високо” бидејќи ова е само едно од повеќето правила кои се земаат предвид. Во некои случаи, функцијата на припадност може да се модифицира од вредности еквивалентни на придавките. Тие вредности можат да бидат “малку”, “многу”, “приближно”, “речиси” итн. Овие оператори можат да имаат прецизна дефиниција, иако нивните дефиниции можат да варираат во различни имплементации. Практично, вредностите на непрецизните множества можат да имаат неколку услови кои се поврзани со операторите И, ИЛИ, или НЕ. Ако се користи И тогаш се земаат минималнте тежини на сите услови,додека кај ИЛИ се земаат максималните вредности.Исто така се користи и НЕ оператор со кој се одзема вредноста на функцијата на припадност од 1 за да се добие комплемент. Постојат неколку начини за да се дефинира резултатот на правилото, но еден од најраспостранетите е мин-макс методот за заклучување, со кој функцијата на припадност ја дава на излез вистинската вредност изгенерирана по пат на спогодба. Правилата може да бидат разрешени паралелно во хардверот или секвентно во софтверот. Резултатите од сите правила кои се вклучени се дефазифицирани во крисп вредност преку еден од неколкуте методи. Теоретски постојат повеќе методи, секој со своите предности и недостатоци. Централизираниот метод е прилично популарен, во кој центарот меѓу резултатите ја обезбедува крисп вредноста. Друг пристап е тежинскиот метод каде се зема вредноста на најголемиот учесник, односно на оној кој е најмногу вклучен во проблемот. Централизираниот метод го фаворизира излезот кој опфаќа поголема област, додека тежинскиот метод го зема оној со најголема вредност на излезот. Следниов дијаграм го покажува мин-макс заклучувањето и централизираната дефазификација за систем со влезни променливи "x", "y", и "z" и како излез е земена променливата "n". Вредноста "mu" е стандардна вредност за вредноста вистина во непрецизната логика.
Забележете како секое правило обезбедува резултат во вид на вистинитосна вредност на одредена функција на припадност за излезната променлива.Во централизираната дефазификација вредностите се резултати добиени од OR функцијата, се максималните вредности кои се користени, но не се додадени и резултатите се комбинирани користејќи централизирани пресметки. Дизајнот на непрецизниот контролен систем се заснова на емпириски методи, во основа плански пристап до trial-and-error. Генералниот процес е како следново:
- Да се документираат системските операциски спецификации и влезови и излези.
- Да се документираат непрецизните множества на припадност за влезови.
- Да се документира множеството на правила.
- Да се одреди методот за дефазификација.
- Да се стартуваат тестови за да се валидира системот, да се додадат детали ако има потреба.
- Да се комплетира документот и да се пушти во производство.
Како поопшт пример, ќе го разгледаме дизајнот на фази контролер за турбина на пареа. Блок дијаграмот за овој контролен систем е прикажан подолу:
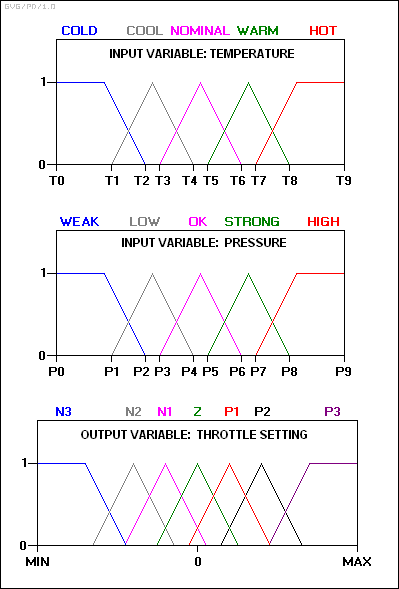
Влезните и излезните променливи се мапираат во следниве непрецизни множества:
N3: Многу негативно. N2: Средно негативно. N1: Малку негативно. Z: Нула. P1: Малку позитивно. P2: Средно позитивно. P3: Многу позитивно.
Множеството на правила вклучува правила како:
правило 1: АКО температурата Е студена И притисокот Е снижен,
ТОГАШ грлото Е P3.
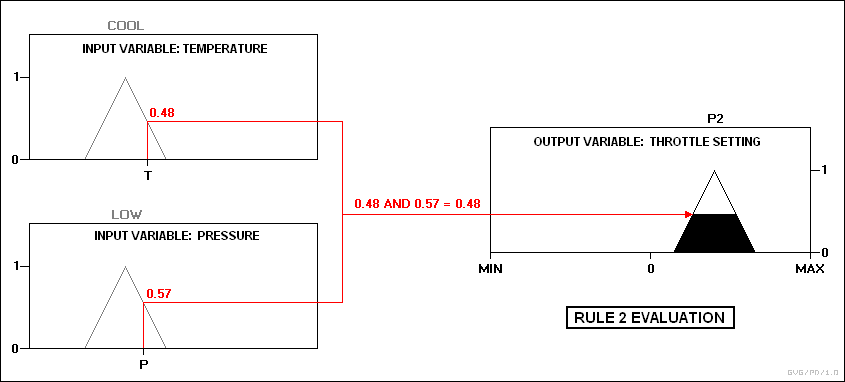
правило 2: АКО температурата Е студена И притисокот Е низок,
ТОГАШ грлото Е P2.
правило 3: АКО температурата Е студена И притисокот Е ок,
ТОГАШ грлото Е Z.
правило 4: АКО температурата Е студена И притисокот Е висок,
ТОГАШ грлото Е N2.
Во пракса, контролерот ги прифаќа влезовите и ги мапира во нивните функции на припадност и нивните вистински вредности. Овие мапирања потоа се искомбинирани со правилата. Ако правилата специфицираат И функција помеѓу мапирањата на две влезни вредности, како што се прави во примерите, минимумот на двете ќе се користи како комбинација за вистинитосната вредност; ако се користи ИЛИ тогаш се користи максимум. Соодветната состојба на излезот е обрана вредност на припадност на вистинитосното ниво на спогодба.
Двата излеза се дефазифицирани преку централизирана дефазификација:
__________________________________________________________________
| Z P2
1 -+ * *
| * * * *
| * * * *
| * * * *
| * 222222222
| * 22222222222
| 333333332222222222222
+---33333333222222222222222-->
^
+150
__________________________________________________________________
Вредноста на излезот ќе го прилагоди грлото и потоа контролниот циклус ќе почне повторно да ја генерира следната вредност.
Градење на непрецизен контролер[уреди | уреди извор]
Имплементирање на микроконтролер со едноставен повратен контролер:
Непрецизното множество е дефинирано за влезната променлива за грешка "e", и изведената промена во грешката "delta", исто како и "output", на следниов начин:
LP: Многу позитивно. SP: Малку позитивно. ZE: Нула. SN: Малку негативно. LN: Многу негативно.
Ако опсегот на грешка од -1 до +1, заедно со аналогно-дигиталниот претворач кој се користи има резолуција од 0.25, тогаш множеството на припадност на влезната променлива може да се опише многу едноставно како табела, со грешки /делта/излезна вредност во првиот ред и вистинитосните вредности за секоја функција на припадност организирана како во редовите подолу:
_______________________________________________________________________
-1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1
_______________________________________________________________________
mu(LP) 0 0 0 0 0 0 0.3 0.7 1
mu(SP) 0 0 0 0 0.3 0.7 1 0.7 0.3
mu(ZE) 0 0 0.3 0.7 1 0.7 0.3 0 0
mu(SN) 0.3 0.7 1 0.7 0.3 0 0 0 0
mu(LN) 1 0.7 0.3 0 0 0 0 0 0
_______________________________________________________________________
—или, во графичка форма (каде секој "X" има вредност 0.1):
LN SN ZE SP LP
+------------------------------------------------------------------+
| |
-1.0 | XXXXXXXXXX XXX : : : |
-0.75 | XXXXXXX XXXXXXX : : : |
-0.5 | XXX XXXXXXXXXX XXX : : |
-0.25 | : XXXXXXX XXXXXXX : : |
0.0 | : XXX XXXXXXXXXX XXX : |
0.25 | : : XXXXXXX XXXXXXX : |
0.5 | : : XXX XXXXXXXXXX XXX |
0.75 | : : : XXXXXXX XXXXXXX |
1.0 | : : : XXX XXXXXXXXXX |
| |
+------------------------------------------------------------------+
Да претпоставиме дека овој систем ја има следнава база со правила:
rule 1: АКО e = ZE И delta = ZE ТОГАШ output = ZE rule 2: АКО e = ZE И delta = SP ТОГАШ output = SN rule 3: АКО e = SN И delta = SN ТОГАШ output = LP rule 4: АКо e = LP ИЛИ delta = LP ТОГАШ output = LN
Овие правила се типични за цонтролна апликација во која условите се состојат од логичка комбинација на грешки и делта-грешки сигнали, додека последицата претставува излезна команда за контрола. Излезот на правилото може да се дефазифицира со користење на дискретна централизирана пресметка:
SUM( I = 1 TO 4 OF ( mu(I) * output(I) ) ) / SUM( I = 1 TO 4 OF mu(I) )
Сега, да претпоставиме дека во даден момент имаме:
e= 0.25 delta = 0.5
Тогаш ова дава:
________________________
e delta
________________________
mu(LP) 0 0.3
mu(SP) 0.7 1
mu(ZE) 0.7 0.3
mu(SN) 0 0
mu(LN) 0 0
________________________
Ако го вметнеме ова во правило 1 се добива:
правило 1: АКО e = ZE И delta = ZE ТОГАШ output = ZE
mu(1) = MIN( 0.7, 0.3 ) = 0.3
output(1) = 0
—каде:
- mu(1): Вистинитосната вредноста на резултантната функција на припадност за ова правило е 1.Во услови на централизирана пресметка, ова е мноштвото на овој резултат за овој дискретен случај.
- output(1): Вредност(за правило 1) каде резултатантната функција на припадност (ZE) е максимум над опсегот на множеството на излезната променлива. Оваа вредност е независна од вредноста на "mu". едноставно ја идентификува локацијата на ZE во опсегот на излезот.
Останатите резултати даваат :
правило 2: АКО e = ZE И delta = SP ТОГАШ output = SN
mu(2) = MIN( 0.7, 1 ) = 0.7
output(2) = -0.5
правило 3: АКО e = SN И delta = SN ТОГАШ output = LP
mu(3) = MIN( 0.0, 0.0 ) = 0
output(3) = 1
правило 4: АКО e = LP ИЛИ delta = LP ТОГАШ output = LN
mu(4) = MAX( 0.0, 0.3 ) = 0.3
output(4) = -1
Централизираните пресметки даваат:
Податотека:7d0811e646bd99585d69f56f39aacf60.png Податотека:D114024d58382f491e33c6cf4d35830b.png = − 0.5
-- за крајниот контролен излез.
Податотека:0b6f125fc8ae42daef40744b028e6719.png Податотека:E2242f9fbd267917a49e96954e77dead.png Податотека:9eff359a5cc37ef961abfc331973d3a1.png Податотека:9a9798cedd07821cc293efea120d6bb2.png
Библиографија[уреди | уреди извор]
- Gerla G., Fuzzy Logic Programming and fuzzy control, Studia Logica, 79 (2005) 231-254.
- Hájek P., Metamathematics of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, The Netherlands, 1998.
- Mamdani, E. H., Application of fuzzy algorithms for the control of a simple dynamic plant. In Proc IEEE (1974), 121-159.